KEPLER AND VERNADSKY:
Music, Not Mathematics, Is the Measure of the Universe
June 2014
LaRouche PAC Weekly Report
This transcript appears in the June 13, 2014 issue of Executive Intelligence Review.[PDF version of this transcript]

Jason Ross. |
Jason Ross of the LaRouchePAC Science Team hosted this "New Paradigm for Mankind Weekly Report" on May 28, 2014. Lyndon LaRouche and Megan Beets were his guests. Ross first introduced Beets, who began with a discussion of LaRouche's comments on the work of Vladimir Vernadsky.
Megan Beets: I want to pick up from the discussion from last week's show, where you [LaRouche] went through an extensive discussion on the implications of the work of Vladimir Vernadsky, and the thing that really struck me about the discussion, is your insistence that what Vernadsky demonstrated, is that not only is man other than any other living process on the planet that we know, in quality, in power, and in rates of progress; that not only is he other than all of the development of life, up until mankind, but he's also the driving force for the development of life on the planet. And then, you went farther with that, and said, no, man is the driving force, not just of life on the planet, man is the driving force for all development and progress of the Solar System as a whole.
I wanted to read what I found to be a very provocative quote from that discussion. You said: "The process of man's evolutionary development in the Solar System, is the proper measure of what the time is, for the human species, life, and for the Solar System." And, a little bit later: "The fact that we, as human beings, are able to create powers of force on this planet, which reach beyond this planet, and shape the dynamics within the Solar System increasingly: That is man; that is Vernadsky's conception of the role of man.
"That you eliminate time as a determining factor. Time is a determining factor for animals, but once the human species comes into play, time is no longer the determining factor. The determining factor is the human, willful intervention in the process of life on Earth."
And then you follow it up by saying, "We are able, as human beings, to gradually take over from the Sun, manage the Sun, determine what the Sun's intensity will be, because we are now dealing with powers of action, which reach far beyond anything the Sun does."
A few weeks ago, you made a statement which I think is complementary: that the human being does not gain knowledge from the animal part of his existence, from the measurements that he takes via his sense-perceptions, but that all that man actually does know, is his own mind.
I think this is incredibly provocative, and it flies in the face of everything that has been experienced over the past 100 years, in the predominant scientific thinking. Not only are you saying that man is the most advanced process in the Solar System, but the way that man actually progresses and develops, is a self-developing process. He develops and learns from the action of his own mind.
This is an idea that was iterated by Nicholas of Cusa, going back to the Renaissance, where Cusa compares the action of the human mind, to a "living book of law," which is able to read and discover, by reading itself, what the truth should be. And he uses another image, of a "living mirror," in which the images of the entire universe are reflected, and that living mirror must only look at itself, in order to develop conceptions.

LPAC-TV
Megan Beets demonstrated how Kepler’s “discovery” of the Solar System, was founded on his concept of the system of musical tempering, or tuning; and that the musical scale is physical; that it is based on the human perception of beauty. |
This has very interesting implications for the role of Classical artistic composition, in this development of the Solar System. We'll come back to that briefly.
Now, why are these things so provocative? Well, they're so provocative, because they fly in the face of the culture that's predominated over the past 100 years, and because of what happened in 1900. Or, as you've been pointing out, you had the Paris Conference of Mathematics in the year 1900; you had David Hilbert propose—and then this was carried on and attempted by [Bertrand] Russell—that we cancel science, and we replace science, and try to embody physical science and physical chemistry, in a logically consistent description of the universe, known as mathematics.
People don't realize it, but that's dominated people's thinking. We have to reverse that.
Kepler's 'Discovery' of the Solar System
So, what I'd like to do, is go through here, an example for discussion of somebody whose work you've cited quite often, which is the work of Johannes Kepler. And what I'd like to do, is address an issue in Kepler's work, which was pivotal to his discovery of the Solar System, as a solar system. In other words, not just a collection of a sun, and some planetary bodies, which happen to inhabit the same general area of what we call our galaxy, but instead, a conception of the Sun, which is causing the motions of the planets, but not causing them as individual interactions, but as a single, unified process, as a whole.
In order to do that, I want to raise an issue which is not typically considered in the science of astronomy; it's usually considered when talking about the science of musical harmonics, but this was crucial for Kepler's ability to make his discovery, and that's the issue of musical tempering, or musical tuning: the fact that in a musical system, one example being when you tune the notes of a piano, or of any instrument with a fixed tuning, you have to make a decision about how high or low to tune every one of the pitches of those musical scales.
FIGURE 1
THE C Scale 
LPAC-TV |
So, here you see the musical scale (Figure 1), the major scale as written out on the staff, and above it you see numbers. We have 1, representing the lowest note; and then a series of fractions, all the way up to one-half. Let me show you what those mean: In deriving the musical scale, it was known, long, long before Kepler's time, that the notes of the musical scale could be derived with a simple experimental apparatus, the monochord, with a single vibrating string that makes a tone. And you can do this with any single vibrating string, a cello string, a violin string, etc. (Figure 2).
FIGURE 2
The Monochord Divided at 2/3 
LPAC-TV |
FIGURE 3
The Monochord Divided at 3/4 
LPAC-TV |
So, we take the whole string, it makes a tone. What was known, even back into ancient Greece, and perhaps far beyond, is that by dividing that string in whole number proportions—the example I have up here is two-thirds, so I measure and I mark off, two-thirds of the whole string. By stopping the vibration and playing only two-thirds of the string, I get another tone, which is a higher tone. Now, if I play that tone simultaneously with the first tone, it's harmonic, it's beautiful, its consonant.
Similarly, if you take another whole number division of the string: Three-fourths of the string makes a higher tone than the whole string, and it sounds beautiful, when sounded together with the tone of the whole string (Figure 3).
Now, if we go back to our scale, what was found was that each of the tones of the musical scale, and therefore of melodies, can be derived with this numerical procedure—seemingly—and we'll get into that.
A Physical System
Now, already, Kepler had a different idea. Kepler, in his Harmony of the World, attacked the idea directly, that these musical tones were a derivation of numbers. And everybody before him, that he knew of, had tried to explain the fact that the musical scale was beautiful, based on the properties of number—numerical properties, and even going as far as numerology and mysticism, to explain the beauty of the harmonic system.
Kepler said, "No, this is a physical system." And so, just to take again our example of two-thirds of the string, Kepler said, look, this is not a derivation of number; you're dealing with a physical vibrating string and the property of physics. What he said, is these divisions of the string which produce the musical scale, are unique physical singularities of the vibrating string, where we place the division there, and every possible tone that could be played from this string, two-thirds of the string, but also the shorter part of the division, one-third of the string, and the whole string, all three of those tones will be beautiful, when sounded together.
So, he completely flips the idea of the derivation of the musical scale, and bases it on an idea of physical harmony: three tones being united into a single, harmonic whole. So, already, that tells you where he's coming from: He's saying, no, it's physical, and not only is it physical, it's based on the human perception of beauty.
Now, let's go back to our scale. This scale, derived from these proportions, is functional, as long as you have only one singer, or one voice which is singing a melody. But it immediately begins to break down, and that's where the fun starts. And so, I'd like to show just one example of that.
This is an example which Kepler actually brings up much earlier in his life, in his first writing, the Mysterium Cosmographicum, which I believe is more than 20 years before he wrote the Harmony of the World. So, what you see here, is our vibrating string, and above it, we see divisions of the string (Figure 4).
FIGURE 4
The Monochord: Finding the Value of ‘F’ 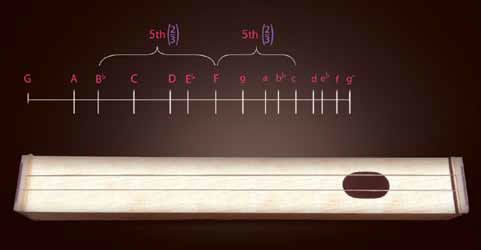
LPAC-TV |
These divisions of the string represent the notes which were written out on the staff of the musical scale. Say we hired a piano tuner to come over to our house and tune the strings of our piano, and what I want to know is how I should tune the note F, which you see in the middle of the diagram here. So, I ask my piano tuner to tune the note F. He has to choose one value to tune that note to. So, as we see, the note F, is five steps of the scale up from the note B-flat, so I tell my piano tuner: Okay, I want you to tune it a fifth, or five steps, up from B-flat. So he does it; he knows that that proportion was the two-thirds proportion I showed you before. He makes the measurement, he makes the calculation, and he tunes the note F.
And then I say, "I want you to check your work, I want to make sure you're right." So, the note F is also five steps or a fifth of the scale, below a higher note, C. So, I say: "I want you to start from that higher note and calculate, and make sure you're right." So, he does it, and he gets a different value [for F]. He gets a note which is slightly lower in pitch than the first note that he had calculated.
Now, this is not an error; it's not an error of calculation. What this points to, is a crucial feature of the physical harmonic system itself, as we see from this very simple example. In this example, I derived two different values for a single tone. I could try to correct the error, and I could maybe choose something halfway in between, let's say, and say, "That's the right one now." But what I would be doing then, is I would be changing the values of these proportions, of these intervals: The two-thirds intervals would no longer be exactly two-thirds.
The 'Comma': Polyphonic Music
I chose to go through only one simple example here, but this is not an isolated example. This gap—where, if we derive the same note from the top down, or from the bottom up, I get two different values—was referred to as the "comma." Now, what we find in the musical system—you could use a similar example, and try it higher in the system, and lower in the system, and you'd run into the same problem—you have commas, you have many different possible values for any single note. Or another way to look at it, is we have different possibilities for the exact size of a musical interval of the scale.
Now, there's no way for the numbers, the mathematical calculations, to choose a value for the musical tone. There's nothing in the fractions and in the numbers that can dictate what the right note is going to be.
Why is this important? Why am I bringing this up? Well, first of all, this wasn't an academic issue. The ambiguity of the musical system, the fact that there seem to be a range of possibilities for the tuning of any particular note, arises as soon as you begin to move away from simple melodies into polyphonic music, meaning that, rather than having a chorus where most of the voices are singing the same thing, or pretty much the same thing, instead, you move to music where you have several melodies, different melodies being sung simultaneously, and they come together into a unity: This was known as polyphony. It had sprung from the Renaissance, and it was taking hold at Kepler's time, and Kepler was completely fascinated with polyphonic music, he was gripped by it. And he was also gripped by the problem that this development in human art, human music, revealed a problem in the system of musical harmonics—he's completely fascinated by it.
The other reason that this problem of these discrepancies is important, is because of where the solution to the problem lies. As I said, there's no possible calculation that can resolve this issue, and determine the exact, right, fixed, tone. There is a process, which can make a determination of what the right tones should be, but it doesn't come in the context of mathematics; it comes in the context of music itself. I just want to show a quick example of that [video clip of Mozart string quartet].

EIRNS/Daniel Platt
In Mozart’s “Dissonance” Quartet, performed here by the Schiller Institute’s Dirichlet Quartet, “the tones don’t preexist. . . . Those tones are generated by a unique, noetic creature, called the string quartet, which is four individuals, tuning into each other, and tuning into the unified idea of Mozart, which is to be unfolded as a unity across time, across the entire composition.” |
That was the opening of a string quartet by Mozart, the K.465, sometimes called the "Dissonance" Quartet [String Quartet No. 19 in C Major]. It's a beautiful quartet where the entrances of each of the four voices, when they come together, make a dissonant tone, which is, yet, incredibly beautiful.
So what did we see? What's the difference? We have four individuals who make up the string quartet, each of whom is playing a line, a melody which is different from the others, and yet they are able to come together into a unified expression; there's a unified motion generating all of the tones. And so, for the member of a string quartet in a good performance, it's not the same kind of ambiguity of pitch. Why is that possible? Well, for the string quartet, the pitches, the tones don't preexist. There's no preexisting, fixed value for the tones which you heard, of the string quartet. Those tones are generated from a noetic process. Those tones are generated by a unique, noetic creature, called the string quartet, which is four individuals, tuning into each other, and tuning into the unified idea of Mozart, which is to be unfolded as a unity across time, across the entire composition.
The musical tones are not determined by some predetermined division of a string, but they're determined by a process of human beings tuning into an idea, and operating as a unity. Now, this process, this noetic solution to what first appeared to be an abiotic problem, or the problem of the division of strings, this creative, human solution is how Kepler solved the problem of the Solar System, and being able to generate a unified conception of the motions of the Solar System.
The Solar System as a Chorus
So, how did he do that? Kepler imagined the Solar System, not as a collection of parts, but as a chorus, or we could say, as something similar to the string quartet. He imagined the Sun and its planets, as a unified process of motions, which were all tuned into a single thought. What you see here is the chart of the motions of the planets, from Kepler's book The Harmony of the World (Figure 5). So you see the planets here in this red square, Saturn down to Mercury, and then, on the outside, which I've highlighted in these purple boxes, you see these musical harmonies written up here. He says, for example, the motions of Saturn make a major third in the scale; the motions of Mars make a fifth, or the two-thirds proportion that we were looking at; the motions of Venus make a diesis, which is a half-step of the scale. And then, he also compared the planets' motions not just to themselves, but to each other: Saturn to Jupiter make an octave of the scale.
FIGURE 5
The Motions of the Planets (from Kepler’s Harmony of the World) 
LPAC-TV |
Now, this is already astounding. But—and here's where the folly of the mathematician comes in—the actual data of the motions of the planets is very close to these musical harmonies, these perfect, whole-number musical harmonies that Kepler wrote out, but they're not exact. And so the mathematician—and they have done this ever since Kepler's time—the mathematician says, "Well, isn't that cute, they sort of come close to a musical harmony; it's cute that Kepler thought he could impose music on the Solar System, but really, we know that's not what's going on. And you see that, because there are errors, there are slight discrepancies from the perfect musical tones."
Now, for Kepler, those discrepancies were the key! Because what those discrepancies told him, is that, "Aha! The Solar System resembles a polyphonic musical process." And he knew that, because he knew what polyphonic human music had done to the harmonic system of musical instruments, to the tuning of musical instruments. And so, he goes through a process of imaging himself being the Creator of the Solar System. And imagining what the motions of the planets must necessarily be, such that each is tuned to the motion of the other, and each is presenting a musical harmony to a viewer who's standing on the Sun. Or to the Sun, which is modulating and generating and causing the arrangement of motions about it.
Now, by doing that, not by looking at the data, not by looking at the astronomical measurements, but by imagining what the necessary motions must be, and what the Sun must be causing in order to have a unified system, Kepler is able to forecast what the motions of the planets ought to be, and what the correct distances of those planets from the Sun ought to be, in order to make those motions possible.
And he was right. And this is what makes the mathematicians go wild: He was right.
So, just to conclude here: The reason I picked this example, is because I think it's a very beautiful example of the fact that human artistic composition is in no way some kind of epiphenomenon of this isolated species, called "human beings." But it's in the discoveries of human culture, it's in the discoveries of human art, of beauty, that man derives conceptions which are in no way separate from our discoveries of physical principle, in the physical universe. And the kinds of discoveries which are generated, not from sense-perception, but by the mind imagining the creative process itself, and drawing from itself, an act of creation and an hypothesis about the creation of the physical universe, this resonates with the physical universe, this gives us power, in and over the physical universe. It's leaps of discoveries of this quality, which have led to the process, which you [LaRouche] have referred to as physical chemistry, man increasing the power of his action over time and coming to dominate processes in the universe.
The Maxiumum/Minimum Principle
Lyndon LaRouche: Well, first of all, as you know, the history of this problem, that Kepler took some musical experts in the operas composed in that period, and he enlisted this troublesome character, and his son, who was much more troublesome than the character was...
Beets: Galileo.
LaRouche: ... And the concept of the mathematician is that the ellipse, or circle, or one of these forms, is the basis for any kind of tuning process. And Kepler, of course, reminded him that that's not the case, and indicated why. Now, the problem is solved.
The way people think in mathematics, they start from a point, and the system is based on a point. Now, this comes out in Kepler's discovery of the very nature of science, that the development of the Solar System is not a system generated from a point! It's a system which has comeexternally to the system of the points! What the mathematician tries to do, is he tries to get a circle or a simple ellipse, or some other simple curved system, and tries to say, let's get different dimensions for these kinds of systems—let's stretch them, let's expand them, let's twist them, and we will therefore interpret this thing by our twisting and so forth, and turning and whatnot, and expanding, this will do it. But it doesn't.
And the universe doesn't work that way, either. The universe works fromoutside the confined area, as Kepler's concept of the question of the Solar System. The Solar System is an entity which is not located in its center, the Sun, as such, but rather the Sun is located within what comes from the outside of that circle or whatever it is. Very simple understanding.
Now, this is exactly what I'm doing, in terms of a scientific program, in dealing with the work of Vernadsky. You see, the ordinary chemist would say, that, we build these things up, from the inside out. We make a formula, we make a construction, which is not what was done by Brunelleschi at all. So Brunelleschi is actually an anticipator of this whole principle. He called it the minimum principle, as against Cusa's maximum principle. The principle of the maximum as against the minimum. And therefore, science came out of that, Kepler came from it, because Kepler was a product of a paradox, which was created by trying to resolve the relationship between the minimum and the maximum.
And so people would try to say, well, Kepler was influenced most by one or the other. Nonsense! He was simultaneously influenced by the fact of the difference between the principle of the minimum, which has no internal center, and the maximum, which has no internal center. But then, the product, when you look at it from the outside of the process, you say that the universe is creating the minor; and you have a reflection of the universe, which becomes the major. And this is a very specific concept, which was defined essentially by Kepler, or actually, Cusa, Brunelleschi, and Kepler.
And so, Kepler then took that idea of the minimum principle/maximum principle, and then applied that, on the assumption that the source of the function comes from outside the object. And that is the fundamental principle which solves these problems.
The musical formation is exactly that. You are assuming, that you're trying to tune this thing to fit an internal formula. That's a mistake! It's a complex function, which confines a whole variety of things, and that is the nature of the organization of the universe. Simple!
But what you described, very accurately, is exactly how that worked, and Kepler was the one who did it. And he had the fight on music, on just exactly this question, the question of tuning.
Beets: Exactly. He had a huge fight with the father of Galileo [Vincenzo Galilei], who was a musician and a music teacher in Venice, and who asserted that there was such a thing as a smallest part, to the musical system. And so, he tried and he tried and he tried, to find the smallest part, and to derive the musical system by an addition of smallest parts. And that's why his music was boring. Because it's impossibl. Music is not a mathematical conception.
LaRouche: Look at the other side, what does this mean? With my presentation in response to what you did: This means that the whole conception of taught physics is fallacious, because it tries to derive from this sense of mathematics. Now, if you look at the behavior of living processes, not a single living process corresponds to mathematics. And yet, the living processes are the processes which, either as human living processes, or much larger processes, are determined not by the division, but by the aggregation. And therefore, the principle of the universe means aggregation. And until Kepler came out with that conception, there was no competent, modern idea of what the universe is, because they were all trying to construct a universe from a point, whereas, in science, you define the point as the victim of the power of the universe.
Ross: There's no minimum without a maximum.

LPAC-TV
Lyndon LaRouche: “The human mind and art and so forth are all the same thing, which is why Vernadsky is the greatest physicist living on the planet today—even though he’s dead! That’s the irony!” |
LaRouche: Exactly. Well, this is what the minimum/maximum meant. And Kepler resolved the relationship of this study, which began with Brunelleschi; and out of this came the study of the Classical Greek, in particular, which came out of Cusa. So it was these two things, which created the crisis which held everything in suspension in the Classical artistic period, until they could resolve that.
The importance of Kepler was that his work gave an example which resolved it. And the example he gave, was by including different universes, as if from a mathematical process, and the complex of these universes and their proper agreement, which makes music and Classical artistic composition, the proper basis for the understanding of true science.
Fun isn't it? It's great! I find it absolutely delightful. This irony, this kind of irony, which I love; I love to tease people, by knowing how stupid they are, and why they're so stupid! Because they work on the basis of an assumption they're taught! They went to school and they passed the course. But then, what they passed, was not what they had eaten! Right?
And, actually, the greatest problem of mankind right now, lies in precisely that matter. And the jerks and the teachers of jerks, and the professors who train the teachers of jerks, all goofed! It's wonderful!
Ross: You think about areas where this approach is needed today, like in the trouble with the quantum, which you know, Einstein—or, was it Planck?—had recognized that ...
LaRouche: Planck!
Ross: Yes, okay. A beginner at the piano might go from one note to the next note to the next note...
Tuning the Universe
LaRouche: Well, that's exactly it: Planck was the minimum, and Einstein was the maximum. It's the same kind of relationship. That's what I've been using, constantly—just exactly this.
You have two extremes. You have one option and you have another one. The most minimal part has the characteristics of the music principle; so does the universe. So it's the relationship, putting these two things, the maximum and the minimum, together, again, which happens when Planck takes the very minimum, physically; and then Einstein complements that with a complete surprise, which had no correspondence to what Planck had done, it seems, but then Einstein comes up with a complement to what Planck's minima was.
And what happens now, you get, suddenly, with these discoveries—and they were known; Leibniz had an instinct on these things, a lot of it. So therefore, what the enemy did, the Satanic people, like the British, and similar kinds of Satanic people, like the Roman Empire, said, wait a minute!
These guys, echoing Cusa, on the one hand, and Riemann as the connecting point, which you know very well, the connecting point to the maximum. And that is the great crisis of physical science today, astronomy and everything else, is the insistence on going to the artificial minimum, because the whole point of Kepler's idea of the Solar System, is that it has no internal center.
Beets: It's true, and the honest fusion scientist and plasma physicists will tell you that that's the problem we're facing in plasma science, in fusion; that is, the problem in thinking to be solved, is that people try to add up the characteristics of the plasma and understand the characteristics of the plasma by knowing the characteristics of each of the particles, and then adding up and mathematically calculating what the results should be.
LaRouche: Yes. The true understanding of the Periodic Table, when properly examined, fits that same paradox. That's the whole business, that's how chemistry works! And mankind is a chemistry specialist, to his living being, the essence of it. It works that way! When you start looking at the chemistry process, the modern chemistry, of the Periodic Table, it's not the Period Table as such. It's periodic all over the place! It's not a periodic table, it's all over the place. You add something to it, it goes into a completely new form, but it always comes from the outside.
Mankind moves, from the small to the very large. And it's the very large that enables him to do it. This is a very simple concept actually, when you understand it. But you have all these idiots who, instead of accepting the fact that there's an enhanced process—. You know, when you can go right from the original triad, of Brunelleschi, Cusa, and Kepler—that's a triad, it's a functional triad, which is a resonance of the universe as a whole. It's not something contained within a sphere, it's something which the content reflects. And the way the content comes into existence is, the universe has done it!
So you have tuned the universe! And the universe is always from the outside, but you learn to play the notes to make the universe resonate, because it will do so automatically, once you get the right solution. That is, really, the essence of the principles of competent physical science, of art, and the human mind, and everything else. But the human mind and art and so forth are all the same thing, which is why Vernadsky is the greatest physicist living on the planet today—even though he's dead. That's the irony!
Oh, this is wonderful stuff! You just put that connection together as an exposure for public attention. Now, many people won't understand it, because they're so saturated with what they were told to believe. But those who are sharp, and young people who are sharp, who are not stupid, who are not stubborn and practical people—practical people are dead people, they just don't know it yet. But creative people will always have an appetite for the resonance of anticipating in their own mind, there's something resonating up there. And they're creative people. People who don't have anything resonating up there, ain't very creative. We leave that to the pigs and squirrels and things like that to take care of.
Beets: And as you've said, this is the true characteristic of man: That's the basis upon which human beings should organize society, the activity of collaborating nation-states, on the planet and beyond!
LaRouche: That's the intrinsic beauty of the human species. And mankind is trying to extend that beauty into expressions which reflect it: That's the nature of music!
Oh, this is fun, this is what I love! I love this irony of all the idiots, who think they have, in their little small-minded mind, that they've got the answer to everything. They've got the answer to absolutely nothing! And the point is, Kepler's discovery, to create the Solar System, to identify it, when it has no center. That the center of the Solar System, lies outside, outside any dimension. Because it's the universe which is creating the Solar System, so you're getting a lawful aspect of the way the universe functions. Riemann is full of this: like the last sentence in his habilitation dissertation, which is a riotous thing for me! I have been laughing about that ever since I first read it.
So that's the problem, and we're dealing with a population which is induced to make itself stupid, by coming up with simplistic explanations of things, that have no simplistic expression. We are part of the universe, and that means, exactly that. That we are a reflection, by the universe, and of the universe. And every part of us, every part of the whole universe, as we know it, is of that nature, insofar as we know these things.
Man, as a Self-Creative Entity
Beets: That means we have to overturn the imperial policy.
LaRouche: Yes, and it means also that black bodies and all these kinds of things, have solutions.
What you've touched upon, by putting this thing together this way, points directly at the right place. And that's exactly the way—guess what? That's what is done by Vernadsky! Vernadsky locates from the outside; Vernadsky says, time as such does not exist. Now, what does Vernadsky mean by that? It means, the truth is in the same principle: Man's development and the whole social process of man's development, is a creative process. That mankind is intrinsically, by nature, a creative entity, a self-creative entity.
Now, man dies, but that doesn't end the process, because actually, the existence of the human being is implicitly universal. The human individual is a universal thing, which lives in history, and only realizes itself, when it's living in history, and history lies always in a higher power, which we call the future. It's the higher development of the higher process, the self-development of the universe. And man is a participant, by resonance, with that progress in the universe. And therein lies the source of the power of mankind as a species, if people would only stop getting stupid and begin to learn a few things. And the precedent of this is Classical music composition, and the way that the composer's mind worked!
What you have to do, is you take the different composers, and you start with Bach himself—and he was not complete; but he was also not unoriginal. He reflected what had gone before him, from the Belgian area and so forth, which was a fertile area; in this one area of these priests, this priesthood, and they developed this system which was then adopted from that inheritance by the Renaissance. That's the picture. The idea of death and birth—birth is more important, but death is a very simple thing: the event has passed, but the event was a process of creation. So what do you do? As a human being, if they're bright, they know they're going to die, but they know they're not going to die. Because the question of death is a question of time. It's the process that counts, the direction of the process, that's what the only value is.
Oh, this is great: This is a very good instrument, and a tremendous heuristic value. And that's what the whole significance was of the Classical musical composition, right? Because this led to a conceptionof the mind. Why is the greatest music, only the great Classical music? The other stuff tends to be junk, which has some intuition of a footprint of something attempted. But great Classical musical composition, is actually immortal, because it has the characteristic in it, which is resonant with the characteristic of the development of the universe. Various kinds of musicians would try to get a universal concept of a physical context of the planets, but the concept of the musical idea of the planets really came from Kepler. It was a plagiarism, or attempted plagiarism against Kepler.
So this is the great principle, which shows you what's wrong with all these poor, half-dead, brain-dead idiots, with popular music: You see what it does to their minds! Listen to the way they talk, listen to the ideas they have, listen to the opinions they have, look at their social behavior. Look at their lack of creativity, look at their fascination with loud monotony. Boom-boom-boom-boom-boom-boom. That's what that is. That kills you! That makes you stupid!
And so, all you have to do is have unpopular music, which is what the popular music is really called.
No, this is it, this is absolutely crucial, and should be developed and elaborated, and should be pounded on and taught, and every part of our organization should understand this. Because it makes everything clearer than any other kind of approach to pedagogy. So let's make sure that that's done, and tell anybody who's beating their thumbs on the table, "cut it out!"... A child can do that, children have done that! If they get a tuning conception of the way they speak, act, and play games, they will pick up on that. And you will probably find that kind of cultural training, proper artistic training, will actually accelerate the development of the thinking powers of the child. So we ought to insist on that: We want our children not to be stupid. Not like Bush people!

