The Secrets of the Florentine Dome
by Karel Vereycken
2013
This article was originally published in French in 2007 at http://www.solidariteetprogres.org/documents-de-fond-7/culture/article/les-secrets-du-dome-de-florence.html, and was translated by the author.
 The Dome of Florence, the symbol of the Renaissance, atop the Basilica di Santa Maria del Fiore. |
 Figure 1. Filippo Brunelleschi (1377-1446) |
“For the wise man, on the contrary,
there is nothing invisible,
alone what is not,
alone pure absence” (Filippo Brunelleschi)
The giant shape of the vast octagonal-based cupola of Santa Maria del Fiore, which dominates the beautiful city of Florence with its 112 meter height, is familiar to many, at least from pictures. On March 25, 1436, the beautiful sounds of a four-voice motet, “Nuper Rosarum Flores,” written by Flemish composer Guillaume Dufay, solemnly consecrated the cathedral: “Recently garlands of roses, despite the savage winter, were given by the Pope, to you, heavenly Virgin, as a perpetual adornment, with a temple of great ingenuity, dedicated in a pious and holy matter” (Box 1)
The two stairways of 463 steps that wind up in between the two shells bring the viewer to the lantern, situated at the equivalent height of a 40-story building. After 16 years and 2 weeks of doggish labor, rising close to 4 million bricks of an estimated 37,000 tons, the dome became the emblem not only of Florence, but of the Italian Renaissance itself.
With a diameter of 42.2 m, its width is nearly the equivalent of the Roman Pantheon (43.4 m) and only slightly surpassed by the Paris grain market (44 m) of 1765. Neither Rome’s Saint Peter’s basilica (42 m), nor Paris’ dome of the Invalids (27.5 m), nor London’s Saint Paul’s cathedral (30.7 m), nor even the Washington, D.C. metallic dome of the Capitol outdo its diameter.
The dome’s realization, seen as impossible at its time, is associated with the name of one man, Filippo Brunelleschi (1377-1446) (Figure 1), a man to whom is attributed the invention of linear perspective. Deceased in 1446, Brunelleschi saw neither the realization of the lantern he conceived, since only finished in 1471, nor the 2.5 m–wide bronze sphere put on top of it by the workshop that trained Leonardo da Vinci, the workshop of Andrea del Verrocchio.
Another architect, Leon Battista Alberti (1404-1472), in the prologue of his treatise on perspective, “De Pictura” (1435), said of him: “Which man, whatever harsh or jealous, would not praise Filippo when seeing this enormous construction rise to the heavens, so vast that it could cover all the people of Tuscany with its shadow, and executed without the aid of beams or wooden struts.”
As we will see in this article, this great building site, challenging all of human knowledge at that epoch, was the locomotive provoking a scientific and technological revolution. Raising the great dome drew new horizons, which far beyond the construction of a building sent ripples and shockwaves of philosophical optimism to the great benefit of future generations.
History of the Project
After 48 years of hesitations, a contest organized to finish the huge building project initiated in 1296 by Arnolfo del Cambio and enlarged by Francesco Talenti on the site of the old church of Santa Reparata set the Dome of Florence in a new direction.
In Florence, everybody was familiar with the final sea-urchin-like shape of the dome, because since 1367 a scale model had been exhibited to the public in one of the side aisles of the growing cathedral. Already that year, two groups of architects had vied in an initial contest. The first one, under the leadership of Lapo Ghini, defended an architectural concept close to the traditional gothic way of building, with rather thin walls and a structure of large buttresses and flying buttresses similar to the cathedrals, capable of supporting the cupola.
The other group, led by Neri di Fioravanti, the architect who built the 18 m–wide vault of Florence’s Bargello prison and the Ponto Vecchio, argued in favor of a solution “al antiqua” (the old way). Neri, as did so many Italians of his day, not only considered buttresses as frankly unaesthetic, but also as belonging to the cultural patrimony of Florence’s traditional enemies—Milan, France, Germany, and other “barbarians” (Goth’s).
Neri proposed, as an alternative to the tasteless buttresses, to encircle the dome with stone and wooden chains, in the same way iron hoops contain the staves of a barrel, an interesting, though inadequate concept, as we will see. The use of metal ties in architectural construction was only in its very beginnings. But already, in rebuilding the choir of the giant Beauvais cathedral after its collapse in 1284, solid iron tie rods were used to link together its buttresses to consolidate the cohesion of its structure.
Neri also planned for the dome the rare but not exceptional use of a double shell, a technique originating from Persia that became typical for Islamic mosques and mausoleums, as the one built in 1309 in Sultanya (Azerbaijan). The interior shell was designed to give the building its structural strength, while the exterior one, besides protection from the natural elements, offered a decisive additional volume.
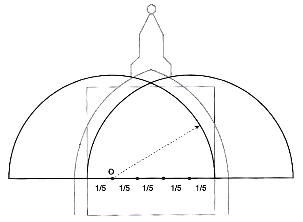 Figure 2 . Diagram of “quinto acuto,” the pointed fifth. The diameter is divided in five equal parts. Raising 4/5 of the diameter makes up the curve of the dome.. |
Far different from the spherical dome of the Roman Pantheon, which is cornered by a huge mass of concrete, Neri projected to raise the curvature of the sections of the shells of the dome according to the Gothic arch, known in Italy as the “quinto acuto” (pointed fifth). That means that one divided the diameter in five equal parts and drew the curvature of the arc of the dome with 4/5 of that diameter (Figure 2).
But from 1415 on, everything was getting ready. With the drum newly built, the building reached already the impressive height of 53 meters, exhibiting a frighteningly vast hole more than 42 m wide. The hour of truth had arrived.
Antonio Tuccio Manetti (1423-1497), author of “The life of Filippo Brunelleschi,” who had met Brunelleschi when alive, reported: “Even more so since the construction masters were already worrying about the difficulty to have to build a vault that wide and so high: seeing its height and width, its weight, its buttressing and supports, arches, and other armatures, which all had to be raised from the ground, it looked in such a fashion that not only the effort seemed awful, but its realization properly impossible.”
To those who invoked that impossibility, Brunelleschi sharply answered that the dome was a sacred building and that “God, for whom nothing is impossible, will not abandon us.” To start the project, he suggested to the wardens of the Opera del Duomo to organize an international conference and invite all the architects, engineers, and masons “as many one could find across Christendom.”
So they did, and during that meeting, “From the words of Filippo, the wardens deduced the verdict that such a building so big and of such a nature could not be terminated and that it had been a naivete, from those architects of the past and of those who conceived the whole project, to believe so. When Filippo said, contesting that wrong opinion, that it could be done, they all answered in choir: ‘How will the centering [falsework] be done?,’ but he insisted again that it could be built without such centering. Since they discussed the matter for several days, it was so that twice, the wardens had him thrown out by their people and the Wool guild, as if he was thinking stupidly and saying only ridiculous things; to the point that he often recalls that during that lapse of time, he didn’t dare to walk in the streets of Florence, having the impression that the people where telling behind his back: ‘Look that foul which has such pretensions!’”
 |
Figure3 . Drawing of a statue at the entrance of Chartres cathedral in France. The donkey playing the harp, taken from Boethius, provokes the audience when he says: “The monument which you contemplate is like this beautiful harp ready to vibrate between your fingers. Will you be able to extract its secret harmony or will you be like me, a donkey with large hoofs, unable to play on it!”. |
In another preparatory working meeting, and before being named “capomaestro” (chief architect) of the building site, they asked him to explain his methods and by what means he intended to execute his design for the titan’s job. Fearing his project would be stolen from him, Brunelleschi simply presented an egg to the audience and said: “The one who succeeds in making the egg stand up, will be worthy of getting the post.” After all tried to do so without success, Brunelleschi crushed the point of the egg on a marble table. All objected that, of course, they would have done the same “if they had known,” and Brunelleschi ironically replied that it would be the same with the dome if he revealed them the nature of his design.
Today, if we examine all the creative solutions invented by the indefatigable Brunelleschi to overcome the scientific problems, in terms of physics, geometry, materials, and machinery, without forgetting the financial and political problems and those of training the manpower to apply revolutionary technologies, then one realizes the decisive share of courage and determination without which genial ideas remain nothing but sweet idle dreams.
Intrigued by the challenge of vaulting the dome since he was a child, Brunelleschi applied solutions ripened over long years and thought-out long before. Because he never committed his ideas to paper, and when he did, only in cipher, the exact way of building the dome will probably remain an eternal subject of speculation. Nevertheless, his unique writing is the dome itself, and the spectator finds himself in the same situation as those challenged by the statue of the “donkey and the lyre” of the Chartres Cathedral (Figure 3). “The monument you see is like a lyre, ready to produce vibrations by your fingers. Will you be capable of extracting its divine harmony? Or will you be like me, the donkey with hoofs, who found the lyre, but incapable of producing any sound with it?”
Centering, or Building Without Wood?
The cupola, as any building, is subject to “pull” and “push” forces known as compression and tension, which the architect has to counteract if he wants to build any vault. Compression, which crushes and shortens the materials, is a relatively minor problem, because one needs an incredible volume before the bricks on the top crush those underneath. It is mainly the lateral thrust provoked by the loading, called “hoop stress,” that is the main preoccupation of the architect (Figure 4).
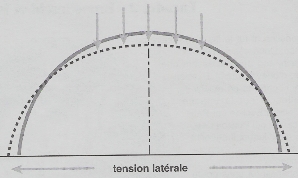
Figure 4. Every architect has to cope with two major constraints: the compression of the materials themselves and lateral thrust called “Hoop stress.”. | 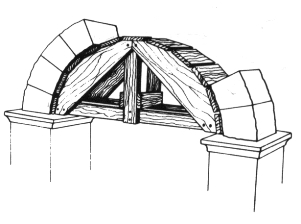 Figure 5. “Falsework” was used to construct both the circular and the pointed arch.. |
In general, to raise circular and pointed arches, a wooden armature was constructed called “centering.” That falsework could only be slowly removed when the mortar was dry and after the insertion of the “keystone” that diverted the tensions from the voussoirs onto the columns supporting the arch. Consequently, wide-barrel vaults or sophisticated gothic cloister vaults appealed to solid centering (Figure 5).
History shows that this technique only appeared during later centuries in highly organized societies able to grow solid wood, or at least capable of having some timber at their disposal.
Otherwise, when solid timber was lacking, domes built without the use of wood did exist, as Auguste Choisy indicates in his “Histoire de l’Architecture” pointing to early tombs in the city of Abydos in ancient Egypt (Figure 6). Using mud-bricks from the Nile’s alluvium that were dried in the sun, domes were erected without wood since the early pharaonic dynasties (3000 B.C.). “Of all types of vaults, the most easily to realize is the spherical vault: the dome is one of the usual forms of the Egyptian vault. The profile is ogival, and the brickwork is composed of plain layers of horizontal beds, real rings of bricks whose diameter gets increasingly shorter. Each seating shortly overhangs the preceding one so that any auxiliary support becomes superficial. As soon as a seating is terminated, it becomes an unalterable crown, ready to receive a new one by corbelling.”
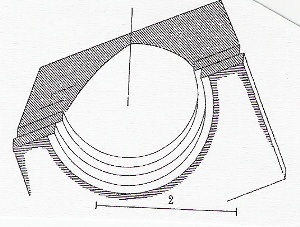
Figure 6. Dome of Abydos in Egypt, 3000 BC. |
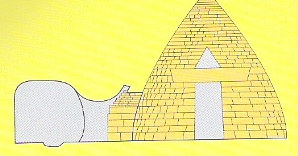 Figure 7. Mycenaean Greece built domes with the shape of beehives. Here, the “Treasury of Atreus.” |
That this building method was not limited to Egypt is proven by the existence of the domes of Mycenaean Greece (1500-1000 B.C.), where the bricks were replaced with stones as in the “Treasury of Atreus,” which possesses a diameter at the base of 14.5 m, and is equally built without centering (Figure 7).
In his treatise on architecture, “De re aedificatoria,” written around 1440 and published in 1452, Alberti affirms: “Yet there is one sort of vault which stands in no need of such machines, and that is the perfect (spherical) cupola; because it is composed not only of arches, but also, in a manner, of cornices. And who can conceive the innumerable ligatures that there are in these, which all wedge together, and intersect one another both with equal and unequal angles? So that in whatsoever part of the whole cupola you lay a stone, or a brick, you may be said at the same time to have laid a keystone to an infinite number, both of arches, and of cornices” (Book III, Chap. XIV).
According to Manetti’s account, Brunelleschi, together with his close friend, the sculptor Donatello, spent several years ferreting in the ruins of ancient Rome studying most of the important architectural remains. Years before the contest, both friends mapped out the dimensions of most buildings, climbing on their tops and even digging out their foundations to the point they were confused with, and nicknamed the “treasure hunters.” By reading the cracks in the walls, they could analyze and admire certain feats and defeats of the late revival of Etruscan building techniques used to magnify Roman grandeur, such as the “Pantheon,” built under Emperor Hadrian in 121 A.D., or the “Minerva temple” and others.
Figure 8. The Pantheon in Rome used the geometry of a globe inside a cube. |
 Figure 9 . Nero’s private “Golden Dome.” |
But in truth, the interior shell of the Pantheon is cornered by a huge buttress of pozzalana concrete (mortar with volcanic ash of Vesuvius) (Figure 8). About 44 m wide and high, the spherical shell starts from brick stone pillars, the famous “locking brickwork” (opus cimenticium) that functioned as coffering. That structure is superseded by circular horizontal layers of concrete amounting to 5,000 tons. Visibly aware of the structural problems involved, the Roman architects ingeniously used tufa, pumice, and even empty clay amphorae to reduce the load of the upper layers while maintaining its structural force.
 Figure10. Vaulting technique without centering from the Gothic period. |
It remains unclear if our two friends succeeded in penetrating Nero’s “Domus Aurea” (golden dome) site where in 1506 the famous “Laocone” was discovered (Figure 9). Nero, after having fire consume the city of Rome, decided to build in 64 A.D. in his villa, a spherical salon on an octagonal base that reached an impressive 14 m diameter.
Building without centering is also documented in a more recent period by the recently republished book of John Fitchen, “The construction of Gothic Cathedrals,” which dedicates an entire chapter to that specific matter. The book shows some of the “tricks,” all acting from the outside of the structure, ignoring the “interior geometry” of the walls, which Brunelleschi will call on (Figure 10).
Arches, Vaults, and Cupolas
A short survey of the building techniques without centering shows that the spherical plane seems to possess one of the required qualities Brunelleschi was looking for—the quality of self-supporting. The “magic power” of curved surfaces is easily demonstrated by a simple experience. Everybody knows that a simple sheet of ordinary letter paper, about 60 gr/m2, is unable to support, let’s say, a solid metal key. But, if the sheet is given a slightly curved inclination, suddenly it obtains that capacity. The power demonstrated does not “emanate” from the nature of its material, but from the power of its geometry. Where I needed a rigid, heavy paperboard to accomplish the work with a plain surface, I can do the same “work” with less material, using a curved surface.
Before going further, it is essential to understand some principles of the arch, because the Florentine dome is sometimes presented as a mixture between the science of domical construction “a l’antiqua,” and the arch building of gothic know-how. After all, as we indicated before, Neri had specified that the shells of the dome should be built according to the “quinto acuto” (pointed fifth) as the usual Gothic arch.
But, as Fitchen notes (p. 80): “As the gothic era progressed, however, a large number of vaults came to be strongly pointed, and this created some trouble, structurally. In a free arch system such as a vault, which carries no surcharge and therefore only supports itself, the line of pressure is an inverted catenary curve. If one envisages a chain or cable suspended loosely from two points that are at the same level but separated by much less distance than the length of the chain, each link then constitutes an identical unit of weight along the curving loop of the chain and is in tension with its neighbors. Together, these links form a curving line whose axes is in the line of stress—in this case, the line of tension—in the freely suspended chain. If this loop of chain were considered as being rigidly fixed so that its curve would not deform, and if it were then inverted, each link or unit would now be in compression with its neighbors, and the axis of the curving line of units would be the line of pressure. This is what happens in an arch, where the voussoirs constitute the ‘links’ of the catenary curve.”
Already in 1734, Pierre Bouguer seems to have studied that principle because it appears in his “Théorie de voûtes.”
Today, in a very pedagogical way, an American school in Winnetka, Illinois, gets students to build arches from paperboard, designed after an inverse catenary curve, permitting them to relive the discovery of that principle (Figure 11).

Figure 11. Constructing a vault without centering: a children’s game when one uses the catenary! |
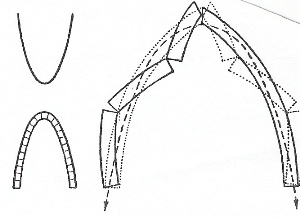 Figure 12. If the shape of a vault is not obeying the invisible trail of a catenary, lateral thrust will make it collapse. |
Concretely, if we apply the catenary principle to the gothic arch, we can observe that if our arch takes a form or proportion going outside (at the extrados or intrados) of the “invisible trail” of the catenary curve, the lateral thrust will provoke a rupture unless compensated by a supplementary rigidity of the materials employed. Deprived of the flexibility of the chain, the top voussoirs will buckle over if the arch is too high and implode when it is too low (Figure 12). While lacking static stability, the catenary is in principle more efficient, because gravity is harmonic with its physical geometry.

Figure 13. Arch of Ctesiphon, Taq-i Kisra palace, close to Bagdad, Iraq. |
After the arch, we can move now to the vault. Catenary-shaped barrel vaults exist, such as the Taq-i Kisra of the Palace of Ctesiphon (Figure 13), close to Baghdad in Iraq, which dates from 531 A.D., sadly damaged when flooded by the river Tigris in 1985. It is built on the same principles as the barrel vaults of the granary of the temple of Ramesseum (Figure 14), close to Thebes in Upper Egypt, dating from the Thirteenth Century B.C. The layers of brick are erected vertically, or diagonally leaning against a solid wall absorbing most of the lateral thrust.

Wikimedia Commons http://commons.wikimedia.org/wiki/Category:Ramesseum?uselang=en
Figure 14. Granary, Ramesseum temple, Thebes, Egypt (Thirteenth Century BC). |
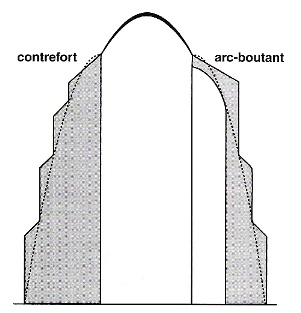 Figure15. The structural strength of gothic buttresses, eventually “emptied,” if they followed the powerlines of catenaries.. |
What has to be understood here is that to be able to load the catenary vault with static load going beyond its own weight, some kind of auxiliary supports are unavoidable. This explains the imposing presence of buttresses and “flying” buttresses in gothic architecture, which take away the pressure from the walls. Nevertheless, it seems that these buttresses are preferably organized harmonically with the catenary (Figure 15).
But let us repeat it once again: A vault following the shape of an inverse catenary “does nothing but support itself.”
Concerning the dome, we have read many authors and tried to find out the exact shape of the angular ribs of the octagonal roof. Because every source says something different (e.g., circle, ellipse, catenary, or tractrice), it seems urgent to redo the measurements as to be clear about what we are hypothesizing.
However, what is known is that in Brunelleschi’s time, one of his detractors, Giovanni di Gherardo da Prato, accused him of threatening the safety of the construction by his ignorance and for not having respected the “quinto acuto” outlined in the contract.
Da Prato, filled with utter jealousy, didn’t hesitate to lambaste Brunelleschi: “Oh deep pit, dark of total ignorance, miserable animal, and so laughable who wants to make the uncertain visible to all, thy absurd alchemy is without great power....”
Brunelleschi, amused, replied with his own poem: “Since the heavens gave us high hopes, oh you, whose animal-like appearance is visible, every man can at last abandon the corruptible, and dispose in everything with great power. Who wrongly judges about this, looses all his assurance, since he doesn’t confront anything terrible to him; for the wise man, on the contrary, there is nothing invisible, alone what is not, alone pure absence. The artist doesn’t see the twaddle of the fool, but he sees, if he doesn’t have wrong judgments, what nature hides underneath its cloak....”
Beyond the anecdote, the poem demonstrates Brunelleschi’s great passion to discover a universal “invisible” physical principle, that he is about to unveil, since hidden by Mother Nature. As we will demonstrate, Brunelleschi and his friends mastered the physical principles of the catenary, both in the domain of the visible and the invisible.
To summarize what we have discussed till now, Brunelleschi, who had to build a dome able to support the considerable weight of the crowning lantern, was confronted with the following bottlenecks:
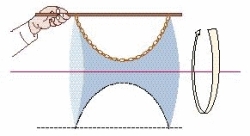 Figure16. The volume created by a rotating catenary, the catenoid. |
1. Buttresses were outlawed by the contract, but also, because the dome had to be raised starting from the height of 53 m, no space remained available to build heavy buttresses that had to rise from the ground level.
2. The perfect spherical dome, constructible without centering, by superposing horizontal rings of bricks, would be unable to carry the lantern.
3. A catenary shaped domical vault (in this case a catenoid formed by a revolving catenary) (Figure 16) also did not provide a real solution. Capable of supporting its own weight, it would be equally incapable of supporting the supplementary weight of the lantern.
The “Sphericam Angularem”
This brought Brunelleschi to look for a special structure of physical geometry, a “self-supporting surface,” sufficiently light to support its own weight, but nevertheless sufficiently strong to support the lantern, while stable enough to escape the necessity of centering. But before investigating further applications of the catenary principle in architecture, let us look closer to this concept of “self-supporting surface.” Impressed by seeing the Pantheon in Rome, Brunelleschi’s first approach seems to have been one of the angular sphere, the “sphericam angularem,” meaning how we can transfer, nearly as perspective projection, the self-supporting properties and solidity in terms of geometrical coherence of the sphere onto the eight sections of the octagonal shells.
 Figure17. The dome appears as the product of three domes, two visible ones and a third one, invisible, the “Sphericam Angularem” interconnecting the former.. |
In that sense, one could say that the cupola is composed, not of two shells separated by a void, but of three shells, the third one being what one could call an “imaginary (invisible) spherical shell” (Figure 17).
Even if Alberti wrote the following several years after the year of completion of the dome, it gives a sense of the concepts involved: “You can likewise turn (raise) the Angular Cupolas without a center, if you make a perfect (spherical) one in the thickness of the work. But here you will have particular occasion for ligatures to fasten the weaker parts of the outer one tightly to the stronger parts of that within” (The Ten Books of Architecture, Book III, Ch.XIV).
Rowland Mainstone, a structural engineer, confirms that the interior shell has been built “as if it were a circular dome ... but with parts cut away from both the inside and the outside to leave the octagonal cloister-vault form.”
Brunelleschi and his friends wanted also to rework the traditional use of symbols where circular motion was seen as the expression of divine perfection going at the encounter of rectilinear motion seen as human imperfection. Nicolas of Cusa, building on the geometrical and mathematical challenges posed by Archimedes, will develop this in his “Squaring of the Circle.”
After all, isn’t a church the house of God, a “Domus Deus,” and as such necessarily some kind of interface between man and God? The divine “sphere” “wouldn’t abandon us.”
Brunelleschi and his friends will “climb on the shoulders” of the best thinkers and architects of humanity to create solutions for a seemingly unsolvable problem.
The Harmonic Properties of the Catenary
Absolute master of the ideas of Nicolas of Cusa and Gottfried Wilhelm Leibniz, the great American scientific mind of Lyndon H. LaRouche, when he mounted the dome in 1988 and discussed the matter with Professor Lando Bartoli,[1] immediately identified the physical principle of the catenary as Brunelleschi’s fundamental breakthrough.
But to understand how Brunelleschi arrived at that solution, we have to go back and look again at the properties of the catenary. By playing with it, we perhaps discover the essential properties:
1. Equilibrium
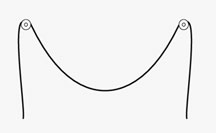 Figure18. A rope hanging in between two nails against a wall. |
If one hangs a chain between two iron pins along a wall (Figure 18), while making sure the chain can glide and find its own equilibrium, one discovers that the shape of the chain depends nearly uniquely on its own length. Going against our common sense perception, to obtain a chain with a bigger “belly,” the chain has to be longer as a whole, and inversely, to have the shape of the chain closer to the straight line, one needs a shorter one. Why? Because the catenary will search its own point of equilibrium, that is to say, the point where the sum of the weight of the two hanging ends equals the weight of the chain hanging in between the pins.
2. Pre-Established Harmony
The equal repartition of tension and weight on each link of the chain is the reason why, if we move a little part of it with the tip of a finger, the curvature of the totality of the chain will be affected and transformed. That phenomenon expresses the least action principle developed by Cusa and Leibniz (see Box 2) and reveals a “pre-established harmony,” such that any event happening in any place affects the rest of the universe; a reality Newtonian physics is unable to explain correctly.
3. Macrocosm and Microcosm
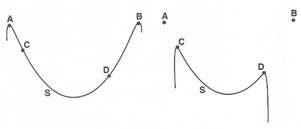 Figure19. If on a catenary formed by ACDB, we drop A and B, the curve formed by CD remains a catenary. |
The preceding principle causes any part of a catenary to be a catenary (Figure 19), because the macrocosm is reflected in the microcosm. If on a given catenary ACDB we drop the ends at A and B, then CD remains the same catenary as before. Inversely, the same principle establishes the fact that any catenary, when suspended between two points, is defined by any of its parts, whatever their size. In the same way the maximum is reflected in the minimum, the smallest part in its turn defines the totality, i.e., the microcosm defines the macrocosm. So when looking to different parts of a catenary, we are looking to different expressions of a global harmonious and equilibrated reality.
A Brick-Stone Self-Supporting Membrane

Figure 20. Stairway between the two domes leading to the top of the Dome. Brunelleschi ordered that the roughcast and herringbone pattern of the brickwork should remain visible for visitors. |
When one climbs up the interior stairways of the dome, one sees that at several precise locations the brickwork pattern has been voluntarily kept visible, while elsewhere covered with roughcast (Figure 20). And because it was Brunelleschi who left us that heritage, one might believe that this was one of the tracks that could lead to unraveling one of the secrets of the dome. But let us not underestimate the illusionist and farce loving character of the personality. After all, he invented perspective, that science of illusion Plato asks us to distrust.
So, it is not a coincidence that we are unable to identify, by looking from the outside of the dome, all the “tricks” of its construction. Already Florence had marveled when the building was being finished and its inhabitants wondered: “How is it possible that it stands up? Where are the exterior supports?”
An analysis of the disposition of the estimated 4 million bricks of all shapes (e.g., triangular, angular) hidden behind the straight tiling on the outside and the frescos from within, leads us to four new major concepts.
1. Invisible Buttresses
Outlawing exterior buttresses, Brunelleschi will elaborate an interior setting to compensate that absence. As specified by a written memorandum deposited at the “Works of the Dome,” reproduced by Manetti:
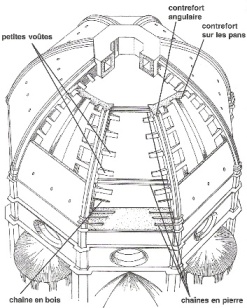 Figure 21. Drawing showing what’s hidden behind the surface of the walls. For Alberti and Brunelleschi, architects should use human anatomy as a model for their constructions. |
“There are 24 ribs (sproni), 8 in the corners and 16 in the sides.... They converge proportionally to the top, where the oculus is. The said 24 ribs, with the said cupolas, are girdled by six circles (cerchi) of strong sandstone blocks. These blocks are long, and are well linked by tin-plated iron [actually lead-lined iron, to prevent rust—KV]. Above said blocks are chain rods of iron (catene di ferro), all around said vaults and their ribs” (Figure 21).
After specifying the precise dimensions and disposition of these elements, he adds: “but the first circle, on the bottom, is also reinforced with long sandstone blocks laid transversely, so that the inner and outer cupolas rest on said blocks. At the height of every 23 feet or thereabout of said vaults, there will be small barrel vaults (volticciuole a botti) from one corner rib to the next one, going around said cupolas.”
These small vaults, in reality lateral “ribs” of the eight buttresses standing on the angles, make it possible to diffuse the hoop tension toward the other 16, and to spread that tension on the totality of the membrane, exerting its “carrying” capacity.
“Below the said system of small vaults from one to the other are big oak beams (catene di quercia), which tie the said ribs. Above each of said timbers is a chain rod of iron (catena di ferro). These ribs are entirely built of gray and tan sandstone, and the covers of the faces of the cupolas are entirely of tan sandstone, tied to the ribs, up to the height of 46 feet. From there on upward the masonry will consist of brick or porous stone.”
While using the same choice of materials as the Pantheon, Brunelleschi’s realization not only takes up Neri’s concept of circling the staves of a barrel, but also goes far beyond.
The lack of oak timber is supposed to explain the presence of only one single “chain” (understand “link”) of chestnut, spliced together with oak clamps. Its precise installment at the highest risk area of the curvature, when the dome is under pressure, suggests something beyond a mere static role. After the earthquake of 557 A.D., wooden links were incorporated into the base of the dome of Santa Sophia in Constantinople at the point where the greatest tension would develop. Quakes would shake Florence in 1510, 1675, and 1895, and while houses fell apart in the city, the dome survived without any major problem, thanks to Brunelleschi’s built-in, anti-seismic device made of stone, wood, and metal.
But for Brunelleschi, his dome was not a barrel, but rather a human body. Manetti reported that Brunelleschi, studying buildings in Rome, “remarked the way of construction of the ancients and their use of symmetry: he identified a type of order similar to flesh and bones, as a man enlightened by God for great things.” Similarly Alberti states, “Lastly, in all manners of vaults, let them be of what kind they will, we ought to imitate nature, who, when she has knit the bones, fastens the flesh with nerves, interweaving it everywhere with ligatures, running in breadth, length, height, and circularly. This artful contexture is what we ought to imitate in the joining of stones in vaults” (Book III, Ch. XIV).
The 24 buttresses can be seen as the bones of a vast thorax, while the chains act as the tendons of Achilles’ heel. But a skeleton will never walk with tendons alone. It needs the muscle that keeps it standing: the brickwork.
2. The Spirals of “Spina Pesca”
Brunelleschi’s second concept will be the organization of the brickwork according to the “spina pesca” (fish bone) pattern, a technique believed to be inherited by the Etruscans that was revived in the Trecento (Fourteenth Century) (Figure 22). The herringbone pattern is shaped by alternating laying bricks in a horizontal way with a vertical setting at regular intervals. These intervals are wide at the bottom, but decrease when going up and even disappear on top. In this way, large spirals travel across the sections and the buttresses from the summit to the base and accomplish a second spreading of stress over the membrane. The lateral thrust of the dome, which concentrates on the joints of its sections, is deviated and absorbed by the “sails” of the membrane. Once again, this technique is designed to induce the properties of the sphere, and notably the solidness of a self-carrying membrane, on the weak panels of the octagonal dome. Have you ever tried to crush a raw egg with two fingers? It’s hard, unless one crushes the edge of it on the table. Maybe Brunelleschi wasn’t joking?

Figure 22. Drawing of brickwork following a “fishbone” (spina pesca) pattern, a technique taken from the Etruscans and redeveloped in Italy during the Trecento. | 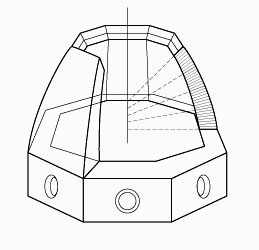 Figure 23. Vertically upward sliding points orienting radial brickwork. |
3. Radial Brickwork
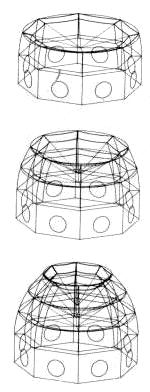 |
Figure 24. (Three drawings showing successive phases of construction) The dome is thought to have been constructed as a succession of rings. |
Quite different from the horizontal corbelling, the bricks of the dome, in reality large tiles designed by Brunelleschi himself, are all radial-oriented toward a focus point one has to imagine “sliding” on a central axis inside the dome (Figure 23). The cutting edges of the vertically laid bricks were supposedly used by a special team in charge of “framing” the orientation of the brickwork with a guiding cord or “trammel.” Seeing the huge scaffolding required to carry the laborers, and on which was installed a specially designed giant ox-hoist in charge of raising the materials, one thinks that the building was raised in “successive rings” (Figure 24). The geometrical arc of the pointed fifth corresponds with the 60 degrees of inclination one finds at the brickwork on the top. If that inclination toward the interior would have been defined uniquely by a single fixed central point at the bottom, the brickwork would have been pushed to the very uncomfortable 90-degree angle, creating problems in terms of structure and centering. As was demonstrated by a scale model prepared by a friend, the rotation of such a trammel does nothing but generate a set of geometrical curves (a hyperbole at the bottom, a parabola at the center, and an ellipse on top), similar to the parabolic geometrical cut generated by a (conical-shaped) pencil sharpener cutting the (hexagonal) pencil. Under no circumstances can a physical, non-algebraic curve result from such an operation. It is known that Brunelleschi used such a trammel; Manetti mentions “a stick fixed at the base turning on itself upwards with the progressive reduction of its inclination” used to build the Schiatti Ridolfi chapel, done before the dome as a testing ground, but whose shape is perfectly spherical.
4. The Catenary Shape of the “Corda da Murare”
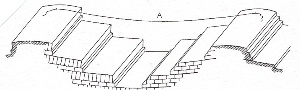 Figure 25. Since ancient Egypt, as in the defense walls of El Kab in Egypt, it was known that layers of bricks following a catenary (hanging rope) curve had extraordinary strength. |
Finally, it is here that Brunelleschi demonstrates his deep understanding of the physical principles underlying the catenary. We have to study the catenary curved inclination of the bricks’ beds in between the ribs. That inclination is sometimes stupidly attributed to the brick workers’ inattentiveness, leaving the “slack line” (corda da murare or building string), used for centuries to guide the beds of bricks, hanging sloppily. Once again, since ancient Egypt, as demonstrated by the defense walls of El Kab (Figure 25), the experience confirmed that catenary curved layers of bricks possess more strength than horizontal ones.
But far from empirical experimentation, it was only the ardent and scientific use of the properties of the catenary that made it possible for Brunelleschi to build the dome. The “world harmony” that exists between each part and its whole gave birth to the self-supporting quality of the building, required to vault such a wide space, carry the load of the lantern, and escape traditional centering. Every brick (microcosm) integrating the physical geometry of the catenary (as the expression of a least action principle) acquires the properties of the catenary, i.e., plays an equal role in supporting the dome (macrocosm). Four million bricks, united in a catenary, do more work than all the buttresses of the universe. With a minimum of material effort, Brunelleschi was able to span a maximum width.
 Figure 26. Italian architect Massimo Ricci built a scale model of the dome in a park in Florence |
 Figure 27. Close-up of Ricci’s scale model showing the herringbone brickwork. |
A question one could raise here is the following: Why a hanging catenary and not a standing, inverse one, as all the vaults we examined before? The answer might be that the harmonic spreading through the catenary principle makes it efficient each way or the other! The hanging catenary brick membrane seems to create a counter-thrust, taking away tension and load from the angular ribs, similar to the negative curvature of the umbrella’s membrane retaining the metallic sheaths. Once again, Brunelleschi’s illusionism reverses our sense-certainties.
A scale model (1:5) about the size of a house was recently built in a park of Florence by a passionate architect, Massimo Ricci, and gives the viewer an excellent idea of the herringbone pattern brickwork (Figure 26-27). Professor Ricci, for his part, did not yet work through the crucial role of the catenary and thinks it is sufficient to use some guiding board, cut in the form of an ellipse generated geometrically by the flower form of the cathedral, symbol of Santa Maria del Fiore.
We recall for Professor Ricci here the fact that even Brunelleschi was in a sense brutally reminded of the forces of the catenary, when during the summer of 1429 wide cracks appeared in the lateral walls of the eastern part of the nave. Instead of building buttresses, as public opinion was screaming for, Brunelleschi used the opportunity to execute Neri’s initial plan. The apsidal chapels around the nave constitute what Brunelleschi called a “catena totius ecclesie” (a chain around the church), capable of absorbing the thrust.
Who Was Brunelleschi?
Brunelleschi was the son of a Florentine notary. Showing early talent for drawing, his father made him a goldsmith (orafo). Passionate builder of clocks and machinery, Brunelleschi had the opportunity to be initiated to Euclid by Paolo Toscanelli del Pozzo (1397-1482), with whom he corresponded during his entire adult life.
Toscanelli, undoubtedly the most fertile polyvalent scientific mind of his time, conducted scientific inquiries in a wide range of domains—mathematics, geometry, perspective, cosmology, medicine, astronomy, and especially geography applied to mapmaking. His 1420 treatise “Della Prospectiva,” unfortunately lost, might have been elaborated with Brunelleschi’s help, who, according to Manetti, was conducting his famous experiments on perspective around the same period. After having shared the school room with Nicolas of Cusa in Padua, where both attended mathematics classes of Prodocimo de’ Beldomandi, Cusa would regularly ask Toscanelli to read his manuscripts before publication, as he did with his “Geometrical transmutations” in 1445 and “Arithmetical complements” in 1450. Toscanelli was often called “Paolo the physician,” because he crowned his studies with a Ph.D. in Medicine; Cusa getting the title of “doctor decretorum.” Toscanelli then became the conservator of the private library of Niccolo Niccoli in Florence. Niccoli was one of the most zealous book collectors of the century, whose collection became the foundation of the famous “Laurentiana” first public library, later integrated into that of the Vatican. Toscanelli was also in direct contact with, and an inspiring influence on Leonardo da Vinci, and it was to Toscanelli that Cusa dictated his last will on his deathbed.
Toscanelli, Cusa, Niccoli, Cesarini, and maybe Brunelleschi himself, were part of a close circle animated by the head of the Camaldulensian order, Ambrogio Traversari, who was entirely committed to bring about the renaissance, with the benevolent support of Cosimo de Medici, great patron of the wool industry.
Traversari, also protector of Piero della Francesca, recruited the young Cusa to organize with him the great ecumenical council that was concluded in the dome of Florence in 1438, to abolish the great schism that had divided for so long Christianity between East and West. They brought in the Vatican such great humanist popes as Martin V, Eugenius IV, Nicolas V, and Pius II. Uniting in a dialogue of cultures all the people of good will under a single vast and beautiful cupola was a powerful symbol calling for an end of centuries of wars and crusades. That dialogue was nourished by an intense mobilization to master the highest of human cognition: How can one square the circle? Let us learn Greek and Hebrew to stop confusing biblical interpretations; let us translate Plato and Aristotle to finally find out the fundamental difference; let us look at the inventions of Archimedes, Vitruvius, and Vegecius; and let us apply the new understanding, building new machinery using new power, starting the wool and paper industry, and printing. And let us defend the general welfare by making hospitals and schools available to the many. In short, let us have a renaissance.
That fight for the good was not always smooth going. By exploiting politically Florence’s military defeat against Lucca in 1433, the oligarchic Albizzi family threw all the blame on Cosimo de Medici and had him thrown in jail, even forcing him into exile to Venice. Having lost his protector, Brunelleschi was arrested under the flimsy pretext he had not paid his dues to the masons guild, a rather usual thing for those days. Two weeks later, the Albizzis were out of power, Brunelleschi was released, and Cosimo was on his way back to Florence. In every battle, Pope Martin V and also Eugenius IV, who will consecrate the cathedral after 140 years of construction, intervened to protect and promote their architectural genius Brunelleschi.
The Discovery of America
 Figure 28. La Pinta, one of the three ships of Columbus’ expedition. |
All of these domains of inquiry—Brunelleschi, linear perspective and “sphericam angularem,” dome-building science; Cusa, “The squaring of the Circle”; The Flemish painter Jan van Eyck, oil painting and a “mappemonde” (world map); his master Roger Campin, painting convex mirrors that appear in that period; Jean Fouquet, Louis XI miniaturist “spherical perspective”; Toscanelli, perspective, astronomy, and cartography—can be united in a single sphere of interest: “non-linear topology.” The practical question always to be confronted, for example, was how to project the properties of a sphere onto a different, sometimes less complex surface. That every breakthrough in one of these domains brought progress to the others, derives from that freedom of spirit called today “pluri-disciplinary de-compartmentalized research.”
 Figure 29. Using a special measuring device on the floor, a gnomon, Toscanelli used the Florentine dome as the largest solar observatory of his epoch. |
Toscanelli was not torturing himself with any formal limitations. Author Ross King writes in his recent book “Brunelleschi's dome,” that in 1475, at the age of 78 and with the green light of the Opera del duomo, Toscanelli climbed the 463 steps of the dome and installed a brass plate with little holes at the oculus of the cupola. With a special measuring device on the ground (Figure 29), Toscanelli transformed the dome into the largest sundial ever built! These observations permitted him to correct all the previous knowledge on the solstices and equinoxes, officially to fix with precision the date of Easter.
Sea travel so far, before the invention of the quadrant and the sextant, was mainly possible through the use of the compass and the astrolabe, designed to measure the angle between the horizon and the Pole Star. However, each observation, to lead to a practical decision for the mariner, needed to be corrected by tables of nautical ephemeredes, in particular the Alfonsine tables established in 1252 in Andalusia under Alphonse X (the wise) by a group of Arab astronomers under the leadership of the Jewish Isaac Ben Sid. Toscanelli corresponded with Regiomontanus (Johann Müller) of Nuremberg (1436-1476), who together with his preceptor, Georg Peurbach (1423-1461), the Austrian mathematician and friend of Cusa, will write up new ephemerid tables for the period between 1475 and 1506. A pupil of Regiomontanus, Martin Behaim (1459-1507), will be the maritime advisor of the Portuguese King Juan II in Lisbon, where we could have met Christopher Columbus. Behaim worked hard on the latitudes and innovated astrolabe building, making them more precise by using copper rather than wood. The oldest world globe known today was built by Behaim in 1492.
 Figure 30. The rediscovery of America was made possible by the rediscovery of the science of sailing on the stars. |
Hence, one could say that Toscanelli’s observations on the top of the dome of Florence gave impetus to the genesis of a new science. Beyond coastal navigation, emerged the rebirth of astronomical navigation (Figure 30).
Already in 1419, the year of the discovery of Madeira, Henri the Navigator had founded a maritime research center at Sagres in service of Portuguese naval exploration. After the fall of Constantinople in May 1453, the road for silk and spices was closed in the East, and the search for new sea routes looked mainly south, in the hope to sail around Africa. But especially Toscanelli had gathered extensive knowledge, through reports from travelers who returned from the Far East. The most prominent one, was an ambassador of “Cathay” (China). As Toscanelli wrote: “In the days of Pope Eugenius (around the Council of Florence), there came an ambassador to him, who told him of their great feelings of friendship for the Christians, and I had a long conversation with the ambassador about many things.”
On June 25, 1474, Toscanelli sent his now famous letter to a friend in Lisbon, Canon Fernan Martins de Roriz, whom he had met before in Florence. Martins figures as one of the participants of Cusa’s dialogue on the “Squaring of the Circle,” together with Toscanelli.
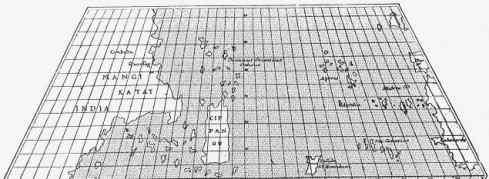 Figure 31 . Reconstruction of the map of Toscanelli given to Columbus. |
Toscanelli assures him that the shortest way to reach Cathay in the East, is to go west. Martins, confessor of the King, then fails to convince his sovereign, but a relative of his family, the young Genoese captain Christopher Columbus, finds Toscanelli’s letter to Martins and decides to write back to Toscanelli around 1480. Even if the valiant Columbus pretended he never made use of mathematical calculations or maps, in his luggage were Toscanelli’s map (Figure 31) and very probably the new tables of ephemeredes, the outcome of Toscanelli’s observations of the sundial of the dome.
Beyond the discovery of America, the science of astronomical navigation gave mankind the power to make thousands of discoveries. Hence, the achievement of the great building of the dome was much more than 37,000 tons of bricks, or a nice esthetical object; rather, its “immortal soul” provoked a wave of scientific revolutions, every day even more profitable for all of mankind.
 |
Box 1: Guillaume Dufay
 Guillaume Dufay. |
Guillaume Dufay was probably born in Beersel, close to Brussels, on August 5, 1397, if not in Kamerijk (today’s Cambrai), where he died in 1474. Present at the Council of Constanz (1414) as a boy in service of Jean Gerson’s preceptor Pierre d’Ailly, he served later as master of the pontifical chapel in Rome, Florence, and Bologna between 1428 and 1437. Dufay gave new life to an earlier technique, the isorhythmic motet.
According to music editor David Fallows, the “Nuper rosarum flores,” composed for the consecration of the dome, “is built on two lower voices that are performed four times at different speeds with the proportional lengths 6:4:2:3, which correspond to the proportions of the nave, the crossing, the apse, and the height of the cupola in the cathedral. That these two voices use the same melody—the Introit for the dedication of a church—at two different pitch levels and with interlocking rhythms itself symbolizes the essence of Brunelleschi’s structural feat, namely an inner shell and an outer shell with interlocking struts. Hence, similar to the effect of beauty that arises from the exterior shell, the motet makes its main musical impact with the lines of the upper voices.”
Box 2: Least Action Curves and Optimal Surfaces
The curvature of the catenary belongs to the domain of physical curvatures, as opposed to algebraic ones, and expresses the “least action” principle. Pierre Fermat (1601-1665) termed it the “principle of natural economy,” characterizing the way light chooses the least time path to go from one given point to another (“Principle of Fermat”).
Leibniz (1646-1716), by taking up the minimum/maximum principle already identified by Cusa when developing the notion of isoperimetry, formulates it as follows: “In all things, there exists a principle of determination one can derive from the idea of a maximum and a minimum, i.e., how a maximal effect is obtained by a minimum of effort. In our present demonstration the time or the site, or in other words the receptivity or capacity of the world, can be considered as the expense, that is, the terrain on which has to be built in the most advantageous way the varieties of forms that correspond to the appropriateness of the edifice, to the multiplicity and to the beauty of its chambers.... In this fashion, a liquid introduced in another one, heterogeneous, takes the form which has a maximal capacity, that is to say the spherical form. Also, in ordinary mechanics, the action of several interconnected weights [i.e., a chain—KV] results in the movement by which finally the largest descent is realized. And in the same way that all possibles strive to exist with equal rights, in proportionally to their heaviness, in the same way is produced the movement by which one remarks the maximum descent of weights, and equally in that same way is given rise to a world in which the maximum of possibles is produced” (“On the ultimate origination of things taken at their roots”).
In 1691, Leibniz notes that Galileo confounded the catenary with the parabola, a fundamental difference demonstrated with precision by Joachim Jungius (1585-1657).
Starting from least action curves, we can move to least action (“optimal”) surfaces and volumes, quite present in nature. The simplest ways to start investigating them are experiences with soap bubbles. One can generate the catenary curve by plunging two parallel iron-wire circles in liquid soap diluted in water. What will appear is the “optimal” volume of a catenoid, generated by a revolving catenary curve (Figure A).

Figure A. The catenary curve generated by plunging two parallel iron-wire circles in liquid soap diluted in water forms the “optimal” volume of a catenoid. |  Figure B. |
When one plunges a dome-shaped structure into the same liquid, one can discover the optimal surfaces that appear on the sections, which form “negative” (concave) curvature, a geometry quite similar to the umbrella (Figure B), and identical to the real structure of the dome, hidden behind the flattened surfaces.
These observations bring us to the conviction that Brunelleschi conceived the cupola from a unique concept of optimum volume based on the least action principle heavily debated at his time in his immediate entourage (including Cusa and Toscanelli).
Lyndon LaRouche remarked that “…The case of Filippo Brunelleschi's construction of the dome of the famous Cathedral of Florence, typifies the axiomatic sources of the achievements of the Renaissance as a whole. If one examines the nature of the problem which Brunelleschi solved, viewing this as would a physicist in the tradition of Leonardo, Kepler, Leibniz, Gauss, and Riemann, one is startled, at first, by the fact that, as early as the middle decades of the Fifteenth Century, the catenary was used, not merely as a form, but as a physical principle of curvature, to solve the otherwise insoluble problem of construction posed. Brunelleschi used a "hanging chain" form, to guide the workmen in the construction. Other ruses of a principled nature, used by the same Brunelleschi, including camera oscura constructions, afford the modern investigator the means to peek inside the cognitive processes which the great architect mustered in the course of the most notable innovations used in his work.” (“On the Issue of Mind Set,” EIR, March 3, 2000).
Footnotes
[1] Lando Bartoli (1914-2001) consecrated a major part of his life trying to understand the structure of the dome. He wrote two books on the subject: “La Rete magica di Filippo Brunelleschi” (1977) and “Requiem per una Cupola” (1988). In 1985, he launched a campaign asking to undo the cement that filled the 48 overtures (60 x 60 cm) of the interior shell of the dome, overtures that were explicitly built to install the scaffoldings supporting the painters doing the frescos. The sealing of these overtures in 1979, a seemingly banal act, proved to have disastrous consequences. The “breathing” (elasticity) permitting a contraction and expansion of the dome, according to the temperatures of the changing seasons, was gravely put into question and ever larger cracks started appearing. It was in the context of a campaign to “Save the Dome of Florence” that LaRouche had an extremely fruitful exchange of views with Bartoli.
Bibliography:
Choisy, Auguste: “Histoire de l’Architecture,” Bibliothèque de l’image, 1899.
Chalifoux, Benoît: “Reflections on Brunelleschi’s dome,” unpublished research paper, 2003.
Director, Bruce: “The long life of the Catenary: from Brunelleschi to LaRouche,” Fidelio, Summer/Fall 2002.
Fitchen, John: “The Construction of Gothic Cathedrals,” University of Chicago Press, 1961.
Gärtner, Peter: “Brunelleschi,” Könemann, Cologne, 1998.
Hamerman, Nora and Rossi, Claudio: “The Apollo project of the Golden Renaissance, Brunelleschi’s dome,” 21st Century, July-August 1989.
King, Ross: “Brunelleschi’s Dome,” Pimlico, Random, Londres, 2003.
Leibniz, G.W.: “Opuscules philosophiques choisis,” Vrin, Paris, 1978.
McLean, Alick: “L’architecture des débuts de la Renaissance à Florence,” dans “La Renaissance italienne,” Editions de la Martinière/Könemann, Cologne, 1995.
Mainstone, Rowland J.: “Developments in structural form,” MIT press, Cambridge, Mass., 1975.
Manetti, Antonio: “Vie, fortune et oeuvre de Filippo Brunelleschi,” dans “Brunelleschi,” Ecole Nationale des Beaux Arts, Paris, 1985.
Marchini, Giuseppe: “Le Baptistère et le dôme de Florence,” Beccocci , Florence, 1972.
Matteoli, Lorenzo: “Ser Filippo Brunelleschi and the Dome,” Nov. 10, 2002, Internet.
Murray, Peter: “The architecture of the Italian renaissance,” Thames & Hudson, Londres, 1969.
Prager, Franck D. and Gustina Scaglia: “Brunelleschi, Studies of his technology and inventions,” M.I.T., Cambridge Mass., 1970.
Scarre, Chris: “Monuments du monde ancien,” Hazan, Paris, 2000.
Tennenbaum, Jonathan: “How Gauss Determined The Orbit of Ceres,” ch.4, Fidelio, Summer 1998.
Vasari, Georgio: “La Vie des Grandes Artistes,” Club du Livre, Paris, 1954.
