The Bourbon Conspiracy That Wrecked
France’s Ecole Polytechnique
by Pierre Beaudry
June 1997
This article appears in the June 20, 1997 issue (Vol. 24, Num. 26) of Executive Intelligence Review and is reprinted with permission.
Never, in the history of science, has there been a more blatant example of the evil methods of the Venetian Enlightenment’s attempt to completely eradicate the Platonic educational heritage of the Renaissance, than the subversion of the scientific competence of the French Ecole Polytechnique.
It is with the advent of the reductionist way of thinking, of what Lyndon LaRouche has identified as “linear classroom mathematics”- otherwise known as the mother of the empiricist-mechanicist-formalist-positivist world view that Pierre-Simon de Laplace and Augustin-Louis Cauchy, in the tradition of Leonhard Euler, were deployed to take over the Ecole Polytechnique. This was done in the name of a British-Venetian oligarchical cabal, whose prime objective was to destroy the nation-state of France, by way of eliminating the education system that had been created by the French Platonic humanists such as Gaspard Monge, Lazare Carnot, and Prieur de la Cote d’0r.
Our aim, here, is not so much to give an account of the positive accomplishments of the Ecole Polytechnique, which has been done in other locations.[1] Our goal is to bring to the light of day the true suppressed story of how the Ecole was subverted, what crimes were committed, and who committed them; and to make known the nature of the epistemological conflict that this precedent created in the history of the tight for scientific knowledge, and technological progress. It is as a result of the destruction of the Ecole Polytechnique’s national education system, that France lost its soul as a nation-state, and was turned into what it is today: a Maastricht bureaucratic zombie state at the service of the City of London, and of the European oligarchy.
In 1814, the Bourbon royal family was put back on the throne of France by one of the most despicable operations of the Holy Alliance among Britain, Venice, Russia, and Austria. This restoration of the monarchy in France was entirely manipulated and orchestrated by a British-Genoese-Venetian conspiracy, whose prime agent from Corsica was the childhood friend of Napoleon Bonaparte, Count Charles André Pozzo di Borgo: the Henry Kissinger of France for the period of l8l4 to 1835.
It is with the advent of this Bestial Alliance that two Bourbon legitimists were brought in, for the purpose of destroying the most competent scientific institution of the French nation-state. The most noble school ever created in France, the Ecole Polytechnique, started to be destroyed, first physically by Napoleon Bonaparte’s oligarchical lust for blood, by sending the Polytechnique students to be slaughtered on the battlefields of Europe, and then culturally and spiritually by Marquis de Laplace, and Baron Cauchy.[2] Systematic, methodical, and surgical menticide was perpetrated by these two royalists, against numerous generations of polytechniciens, from about 1814 on, all in the name of science (see Figure 1).
FIGURE 1
The assault against the Ecole Polytechnique
The crimes political purges plagiarism suppression of ideas mathematical terrorism mental paralysis by limitation menticide |
The criminals Count Charles André Pozzo di Borgo Marquis Pierre Simon de Laplace Baron Augustin Louis Cauchy Auguste Comte |
The weapons political correctness Newtonian and Cartesian dogmatism continuous extension of space-time linearity in the small formalism and algebraic analysis limits of functions secular humanism or positivism
|
Monge and Carnot: an education policy based on ‘enthusiasm’ and creativity
From 1794 to 1814, the Ecole Polytechnique had become without any doubt the leading scientific institution in the world. Founded during the French Revolution, during the years of the Terror, by Lazare Carnot (1753-1823), and Gaspard Monge (1746-1818), the Ecole Polytechnique very rapidly became the center of renewal of the Platonic method of scientific discovery established in France by the Brotherhood of the Common Life in the fifteenth century, under Louis XI, pursued through the seventeenth century’s Colbertian Royal Academy of Sciences with Christian Huygens, Ole Roemer, Blaise Pascal, Gottfried Leibniz, and the Bernoulli brothers, and continued into the eighteenth century by the Oratorian Order which educated Monge in Beaune and Lyon.
 Figure 2. Lazare Carnot’s principle of enthusiasm otherwise known as “agapé,” was the founding principle of the Ecole Polytechnique. |
Monge instituted the Oratorian method of the “brigades,” which was based on Carnot’s principle of “enthusiasm,” in having students relive past discoveries. When discoveries were made with the guidance of the sentiment of agape, that is, the emotion associated with the apprehension of higher ideals, such as love of God, love of justice, love of country, and love of mankind, the brigades were virtually guaranteed to transform uneducated peasants and orphans into the best scientists and trained engineers, within only a few years.
The method virtually assured that the students would acquire, in three months, the constructive knowledge that others would take three years to learn. Both Carnot and Monge emphasized the use of synthetic geometry, thus restoring the heritage of Classical Greek geometry, the heritage of Gaspard Désargues, and Pascal, in the continuation of the geometry work of A.-M. Legendre. The Monge method of synthetic-descriptive geometry became the key to the crash education program which ultimately saved France for a short period of time (1794-1814). Many of the officers of the Ecole became engineers, scientists, and world class geometers and mathematicians, who went on developing science in other countries, such as Germany and the United States. Sadi Carnot, Jean-Victor Poncelet, Jean-Baptiste Fourier, André-Marie Ampere, Louis Poinsot, and Louis Pasteur, were only a few of the great scientists to come out of the Ecole Polytechnique.
The education program of the Ecole Polytechnique was based on universal principles which subsumed and linked together methods applicable to both Arts and Sciences. This is the reason why Prieur de la Cote d’Or (1763-1832), one of the founders of the school, chose the Leibnizian term polytechnique (“poly”=many, and “techne”=trades] for the name of the new school. Its principal mission was to give the new Republic, as efficiently and as rapidly as humanly possible, scientists, and engineers to serve in public works, as well as in the military. Also required were architects, manufacturers, artists, physicists, chemists, etc.; and the polytechnique method of descriptive geometry, instituted by Monge, served as the theoretical and practical epistemological basis for that purpose. Note, as an example, how Carnot, himself a student of Monge, viewed the importance of perspective in drawing classes for beginners. This is, for Carnot, the true source of the Machine-Tool Principle of the Ecole Polytechnique.
“Linear perspective . . . is calculated mathematically [but] aerial perspective … can only be grasped by the sentiment. By comparing these two sciences, where one is sensual, the other ideal, the methodical course of one will help penetrate the mysteries of the other.... [Aerial perspective in painting is] the art of generating ideas by means of the senses, of acting on the soul by the organ of vision. It is in this way that it acquires its importance, that it competes with poetry; that it can, like poetry, enlighten the mind, warm the heart, excite and nourish higher emotions. We shall emphasize the contributions that it can bring to morality and to government; and how, in the hands of the skillful legislator, it will be a powerful means of instilling horror of slavery, and love of the fatherland, and will lead man to virtue.”[3]
 Figure 3. Gaspard Monge, trained by the Oratorian Order, instituted the method of "brigades," in which students relived the discoveries of the great thinkers if the past. |
For Carnot and Monge, the republican idea of freedom was not an idle, empty conceit, a leftist “gotta do my own thing”; it was the centerpiece, the very heart of the national education policy. Because an appropriate method of discovery truly represents freedom from ignorance, freedom to guarantee that each citizen has the potential of increasing the power of mankind over nature, by means of overthrowing previous axiomatic limitations that prevented scientific and technological progress. And this is why the method of discovery was made accessible to every citizen, especially the poor and the orphans, in order to enlarge the pool of contributions that would be put at the service of the nation-state. Carnot made clear that this principle of education was not just for France, but for the whole world. “Elevate to the dignity of man every individual of the human species,” he wrote.
For the Bourbons, Pozzo, Laplace, and Cauchy, however, such an institutionalization of education had to be prevented at all cost. It was as if they had said: “If you educate the masses, they’ll want more, they’ll never be satisfied, and we won’t be able to control them.” And, since the feudal oligarchy needs only about 5% of an educated population to serve them, in the administration of society, the program of the Ecole Polytechnique had to be destroyed. So, the Restoration Bourbons had to figure out how to subvert the' education of freedom through the students’ reliving of important original discoveries of principle. They wished to substitute for that education the Newtonian-Cartesian mechanistic world view.
Cauchy was their prime choice. He was a pro-feudalist type of Jesuit-trained mathematician, and an oligarch. He was stupid, narrow-minded, and fanatical: perfect for the job.
All that Cauchy had to do, was to teach that man’s mind is limited; that all ideas come mechanically from sense perception, and that knowledge is eternally fixed by the algebraic linearity of a mechanical theorem-lattice, the which is guarded by his two main principles: the principle of limits of functions, and the principle of continuity, whereby limits of functions are smoothed out to zero. This was in perfect congruence with the fanatical Cartesian theorem-lattice of continuous space-time. But, for Cauchy to be brought in, the Ecole Polytechnique first had to be rid of Carnot and Monge, and of their policy of “enthusiasm” (agape).
Political purges: unseating Monge from the Academy
After the Treaty of Vienna, essentially written by Pozzo and his fellow Venetian Capodistra, in 1814, Monge and Carnot were stripped of all honors and were removed from their posts by the new Bourbon regime. The story of how Monge and Carnot were removed from the Academy of Sciences is the most disgusting act of political subversion of the whole Restoration period.
The full political power of the restored Bourbon monarchy of Louis XVIII, and later Charles X, was behind this coup. Pozzo di Borgo controlled Louis XVIII; Louis XVIII controlled Marquis de Laplace; and Laplace controlled Baron Cauchy. The conspiracy aimed at removing Carnot and Monge from the Academy of Sciences, and rushing into a membership seat, their protégé Cauchy. This was a most unusual political position for a young man of only 27 years, while Carnot was 63, and Monge 70. The seats of the Academy are usually elected by their members, not appointed by court decree. At any rate, with the reactionary regime in place, it was politically correct to eliminate republican opponents and replace them by royalists; so, both Carnot and Monge were expelled, and Cauchy was appointed to sit in Monge’s chair. The very same year, Cauchy was also appointed by Louis XV HI himself to be professor at the Ecole Polytechnique, forcing Louis Poinsot out. [4]
Replacing Monge by Cauchy, was the signal that a terrific change was about to occur in the Ecole. And indeed, Cauchy took over the instructional program of the Ecole, and thoroughly subverted the high principles that had been established therein for 20 years. Bruno Belhoste, the biographer of Cauchy, makes it very clear that the operation was totally political:
“The forced resignations of Monge, Guyton-Morveau, Hassenfratz, and Lacroix had provided an elegant opportunity to staff the Ecole with politically acceptable scientists. The replacement of Poinsot by Cauchy was obviously part of this great purging enterprise, an undertaking that would culminate, several months later, in the reform of the Ecole Polytechnique. . . These purges were regarded by the Academy, and by learned society in general, as contemptible affronts. Carnot and especially Monge were respected scientists, first-rate minds. Cauchy nevertheless accepted his appointment without hesitating.”[5]
The political correctness of this oligarchy went as far as renaming the Academy, the “Académie Royale des Sciences,” and the Ecole became the “Ecole Royale Polytechnique.”
Plagiarism and suppression of ideas
Baron Augustin-Louis Cauchy (1789-1857) gained his title of nobility for his services to the Bourbon King, and, in 1816, he was given the opportunity to destroy French science, by literally suppressing and plagiarizing scientific discoveries. A mathematician by profession, Cauchy was put officially in control of proofreading the latest discoveries at the prestigious French Academy of Sciences. He is variously described by C. A. Valson, according to N. H. Abel, as “a bigoted, selfish, and narrow-minded fanatic.”
As a Bourbon legitimist, Cauchy had a profound hatred for republican ideas, and especially the idea of having a national education policy of developing the creativity of the citizens, especially the poor and the orphans. He had an elitist approach to education, as the Jesuits advocated, whereby only a privileged few would have access to higher education.
Cauchy’s analytical method, based on and further extending the subversion of Leibniz's calculus carried out by Leonhard Euler in the century before, was aimed at destroying human emotions as expressed by Lazare Carnot’s “poetic principle” of discovery “guided by sentiment.” For Carnot and Monge, scientific discoveries guided by this sentiment of agape were the foundation of education; for Cauchy, algebra was the means of destroying such passionate emotions.
Among several nasty operations, Cauchy is notoriously responsible for two of the most famous scandals in the history of mathematics, when he suppressed the works of Niels Heinrik Abel (1802-29) and a young republican activist Evariste Galois (1811-32). [6] As detailed by Felix Klein and E.T. Bell in their historical works, Cauchy, acting as the responsible authority for the French Academy, was given, for review, Abel’s original papers in 1826. Cauchy reported that he had lost the papers.
But, when C.G.J. Jacobi. who had been apprised of the content of these papers, learned from Legendre what Cauchy had done, he wrote him a letter of protest, dated March 14, 1829: “What a discovery is this of Mr. Abel’s. . . ‘? Did anyone ever see the like? But how comes it that this discovery, perhaps the most important mathematical discovery that has ever been made in our century, having been communicated to your Academy two years ago, has escaped the attention of your colleagues‘?”
The Norwegian government was informed and intervened, but the Abel manuscript was nowhere to be found among Cauchy’s papers until the Bourbons were overthrown, in 1830, and Cauchy was banished from France with the King.
In matters of scientific honesty, it is normally unacceptable, at least in civilized countries, that a scientist use someone else’s discoveries for his own aggrandizement. But this did not restrain Cauchy from indulging in borrowing other people’s ideas. Indeed, Cauchy had the bad habit of “adding” to his own discoveries innumerable ideas that were taken from papers which were submitted to the Academy. In Cauchy’s reports to the Academy, some authors were quoted, some were not. Commentators or Cauchy’s biographers considered this “discreet overlapping,” or “deepening” the understanding of other people`s theories, “broadening or generalizing” other authors, without recognizing their merits. I f only Cauchy had improved upon them!
Similarly, Galois had submitted his paper to Cauchy in 1828, and again, Cauchy “lost” the manuscript. Abel’s work was not published until 1841, with strong insistence from the Norwegian government. Galois’s work did not appear until 1846 through the efforts of Ampere’s protégé, Liouville. During the intervening years, Cauchy made free use of these “lost papers.” Incredible as it may seem, Cauchy published, as his personal discovery, the proof of a theorem that will later be found to correspond precisely to the “Galois theory." [7]
Breaking with the concept of continuous extension
Another case of sheer intellectual terrorism, was Cauchy’s conflict with Jean-Victor Poncelet (I788-1867), a student of Monge who is recognized, today, as the creator of projective geometry.
In 1820, and also in 1828, Cauchy reported back to the Academy of Sciences on two papers, each of book length, representing the life‘s work of Poncelet, which were first drafted during his incarceration in the Russian prison of Krasnoi, eight years before, during the Napoleonic retreat from Moscow. The two revolutionary papers, which later became the basis for the Traité des propriétés projectives des figures (Treatise on the Projective Properties of Figures) were written in the spirit of the descriptive geometry of Monge and of the geometry of position of Lazare Carnot, in such a way as "to free geometry from the hieroglyphics of analysis," as Poncelet put it.
Although Cauchy, who was the rapporteur, could not find anything wrong to say about the author`s very detailed new revolutionary discoveries in projective geometry, he could not handle the paradoxes represented by Poncelet`s crucial function of the “principle of continuity." As Poncelet put it, “These quibblers or sophists had a total horror of the infinite and of all mutations in the signs of positions."[8]
Cauchy had a formalistic, limited scope of what the human mind could do. On the other hand, Poncelet knew that there were no limits to the power of the human mind’s capacity to make discoveries. One of his most important discoveries relates to this principle of continuity, whose function l will simply identify here for the reader.
Poncelet’s principle of continuity relates to the continuation of the geometric properties of projection beyond the finite and the visible into the realm of the "ideal" and of the "infinite." Because Poncelet’s concept was never made “exact" for the algebraists, who constantly avoided pushing their own thinking to the limit, Cauchy claimed that Poncelet’s principle was mysterious and incomprehensible, and therefore should be entirely discarded. On the other hand, Cauchy's concept of continuity merely indicated “a linear function which constantly takes one finite value between two given bounds.”[9]
This shortcoming, however, could have been overcome by simply recognizing that the Poncelet “principle of continuity" implies a paradox, everywhere it applies, and that such paradoxes are crucial discontinuities, mathematical singularities, just like crucial discoveries in music, art, or poetry.
Poncelet believed, that unless each particular discipline is brought to the limit of its axiomatic underlying assumptions, the human mind cannot progress. For him, the sentiment of true geometry implies l) the mastery of the underlying principle of a given discipline; 2) the application of the same principle to another discipline; and 3) the generalization of that underlying principle to all human disciplines. The principle of continuity, therefore, is understood as a sort of limiting function that would lead to a sort of jump function that permits you to go from one level to the next higher universal. Thus for Poncelet, when a paradox occurs, at the limit of a theorem-lattice, it is like an anomaly which is attached permanently to the geometric relations of that lattice.
What Poncelet is addressing is, for the first time, the introduction into projective geometry of the notions of “ideal” and “infinite” projections, which went beyond the merely visible, such as the paradox of two parallel lines meeting at an “ideal” point at infinity. Of course, there is no such point out there, at infinity, except as an anomaly, a paradox which shows the limitation of the Euclidean plane, and raises the question: What is beyond that apparent limit? What is a non-Euclidean geometry? And we know that the answer to these questions will begin to be answered later by Carl Gauss and Bernhard Riemann.
From the standpoint of Riemann and Gauss, Lyndon LaRouche has, in the last 40 years or so, developed the full epistemological significance of such mathematical discontinuities in economics, that is, with respect to the increased power of mankind over nature. He has shown that the paradoxical “continuous function of discontinuities” has a critical role to play in discoveries as discontinuities in the human creative process, that is, in the power which permits one to go from a lower level of hypothesis to the next level of higher hypothesis, from a lower manifold to a more universal manifold, and from there to hypothesizing the higher hypothesis.[10]
Properly understood, such developing powers of new hypothesis mean true freedom. “That if you study mathematics, as it is generally taught in universities today, as most mathematicians will present it to you, then you are not free: you are a slave of a curvature, which is a linearized curvature, called linearization of the small, which you impose upon yourself. You have no freedom. You have no scientific judgment beyond what linearization permits you to adopt.” [11]
The use of such paradoxes by Poncelet had the effect of causing major disruptions in the theorem-lattice of Cauchy, because it had the power to break up the linearity of his algebraic form of thinking. And this, Cauchy was not ready to accept.
Poncelet was the foremost scientist to polemicize so forcefully against Cauchy’s abuse of algebraic analysis. Recalling the negative effect that Cauchy’s method had on students, Poncelet wrote:
“Such a way of proceeding [algebraic analysis], while it is reminiscent of the Ancients, without being better, gives much too much preponderance to particular facts over general facts; it breaks the link between theory and ideas, substituting a given series of theorems, recipes, so to speak, of the science of the discrete numbers. Obviously, one could not impose such a method as a model without for- getting the true aim of Mathematics, and without taking the chance of bringing us back to the scholasticism of the Middle Ages, whose narrow spirit has been … much too propagated in the teaching in our high schools and colleges.”[12] But, by 1826, because of his relentless fight for the truth, Poncelet was so isolated from the scientific community by Cauchy that he had to resort to publishing his works in Germany, in Crelle’s Journal. From there, Poncelet will have seminal influence on the future development of geometry, especially in the cases of Jacob Steiner, and his student, Bernhard Riemann.
But Cauchy’s service to the oligarchy was not limited to science. In helping to establish the post-1848, New Holy Alliance Order, Cauchy became the leading continental propagandist for Britain’s Crimean War. According to E.T. Bell, Cauchy attacked both “Muscovite ambition and Mohamedan fanaticism.” “The Jesuit Council, grateful for Cauchy’s expert help, gave him full credit” in preparing “the regeneration of peoples brutalized by the Koran .... The net result of the work was the particularly revolting massacre of May 1860. Cauchy did not live to see his labors crowned.”[13]
Laplace, the Newton of France
Cauchy was not the only oligarch guilty of crimes against the Ecole Polytechnique; Laplace was his superior and controller. Marquis Pierre-Simon de Laplace (1749-1827), while apparently adopting an extreme diversity of political persuasion – depending upon who was in power in France – throughout his long career as both a French government official and a mathematician in the French Academy of Sciences, nevertheless remained true to the principles of Cartesian philosophy.
Laplace is known as the "Newton of France,” for having championed Newton’s work on the continent versus that of Johannes Kepler, Huygens, and Leibniz, as seen in his Celestial Mechanics. He is also credited with founding modem probability theory.
Together with fellow academician Joseph-Louis Lagrange, Laplace suppressed the work of Jean-Baptiste Fourier on the “wave” theory of heat, from 1807 to 1824. This Fourier work represented a direct attack on the algebraic approach of the Newton-Descartes cabal. The polemic not only threatened to revive the “transcendental curves” approach of Leibniz, Bernoulli, and Nicolas of Cusa, but was also directly congruent to the efforts at reviving the traverse wave theory of light of Leonardo da Vinci and Huygens. Only when Fourier became the head of the Paris Academy of Sciences, in 1824, was his work published in the Academy’s Mémoires.
Not until the work of Young and Fresnel demonstrated that Huygens was right and Newton was wrong, about the wave nature of light, did Laplace recognize the necessity of reformulating the Newtonian-Cartesian framework. In particular, he was forced to realize that the results of electrodynamic research, as initiated by Benjamin Franklin and his collaborators, could no longer be contained.
Laplace promoted his friend Jean-Baptist Biot, whose “simply-connected” Biot-Savart law for the interaction between electrical current elements, was the counter to the “multiply-connected” law of fundamental electrical experimentalism of A.-M. Ampere and Wilhelm Weber. And in fact, what is represented as Ampere’s law in modem mathematical physics texts is a total, unmitigated fraud. As recently detailed by Laurence Hecht in 21st Century Science & Technology[14] , and in Jonathan Tennenbaum’s introduction to that article, this continuing fraud represents an essential barrier to any substantial progress in contemporary microphysics.“ And in fact, it is the electrodynamics of Ampere, Gauss, Weber, and Riemann which leads to the emergence of atomic and nuclear science. The question involved is not one of differing formulas to represent a physical phenomenon, but rather one of method of hypothesis, as Gauss insists in his 1845 letter to Weber.
In brief, Benjamin Franklin not only sparked the greatest political revolution in history, but also revived experimental science in the mid-eighteenth century with his electrical investigations. [15] With the demonstration in 1820 by Hans Christian Oersted of the effect of an electric current on a magnet-that is, the experimental demonstration of the effect of electric currents on magnets-it was immediately recognized by many of the remaining scientists of the Ecole Polytechnique that this could provide the means of realizing Franklin’s program for an electric telegraph, a technology that was essential for the defense of the young American Republic. The scientific framework for this was created by Ampere by the mid-1820s, in the face of growing opposition directed by Laplace. This work was then transferred to the United States under the direction of Alexander Dallas Bache, the great-grandson of Benjamin Franklin, which led to the development of the essential technological means by Joseph Henry.
At that point, in 1828, Alexander von Humboldt, the close collaborator, and in many ways, the international successor of Benjamin Franklin, brought together in his home in Berlin the world`s then leading scientist Carl Friedrich Gauss and the young experimentalist Wilhelm Weber. By 1833. Gauss and Weber had constructed the world`s first practical electric telegraph.
In 1837 the Holy Alliance`s Metternich ordered that this dangerous work of Gauss and Weber be shut down--just a few days before Bache was scheduled to meet with Gauss. From that point until today, there has been a complete pogrom against the electrodynamics of Ampere, Gauss, Weber, and Riemann. In its place, we have the field theory of James Clerk Maxwell – though actually, it was Laplace and Cauchy who generated the essential ingredients for this scientific fraud, in their original battles with Ampere.
The issue is the dogma that all questions of science are resolved eventually through mathematical proofs demonstrated upon a blackboard, or, a computer. But as Gauss insists, mathematics is the "queen" of science, while physics is "king." All mathematical formalisms are, and will always be, incomplete. It is the method of hypothesis only which is substantial. The primary historical fact of mathematical physics practice is that each discovery of new physical principle, demonstrated by properly designed "crucial" experiments. of which Ampere`s are exemplary, presents mathematics with absolute discontinuities. What Gauss insisted upon as the "vital question for Ampere`s entire theory," are today referenced as electrons and protons. But really for Laplace, at the time, Ampere`s theory and electrodynamic experiments represented the nightmare of` the resurrection of Kepler`s quantum field method of discovery.
Laplace had led the fight against the revival of Huygens`s and Leonardo Da Vinci`s wave theory of light, as seen in his suppression of the work of Fourier. But, by the early 1820s, Laplace recognized that the Newtonian fraud could no longer be maintained. And in fact, in 1824, he had one of his henchmen who had fronted the attack on Ampere, Biot, publish letters demonstrating that Sir Isaac Newton had gone off his rocker in 1692-which also marked the end of Newton's practice of witchcraft. Instead of Newton, Laplace recommended the work of Cauchy.
Cauchy had already “reformed" Leibniz`s calculus through the application of Euler`s series representation of mathematical functions. While series representation of mathematical functions can prove useful for engineering applications, in terms of fundamental science, the idea that adding up a series of terms, even an infinite series, to fully represent a causal relation, has no more substance than the delusion that simply combining the proper number, sequence, and type of dead chemical molecules together in a laboratory flask can in any way lead to the generation of a living being.
The Leibnizian approach of Ampere and Weber was adopted by Gauss and Riemann in their geometric approach to functions of complex variables to electrodynamics, while that of Laplace was imposed later through the fraud of Clerk Maxwell and his artificially preconceived analytic functions imposed on natural phenomena, as the ultimate explanation for mechanistic causality. “But what is so wrong with a formal, analytical, mathematical physics?" you might ask. Well, you have to go outside of mathematics, into real life, to answer that question, and discover that mathematics cannot be made to be a universal tool applicable to science, because, then, the human mind is destroyed.
Mathematics as epistemological warfare
By 1816, the polytechnique method of Monge and Carnot was totally subverted and reorganized by Laplace and Cauchy, who both considered the sublime program of Monge to be chimerical. The method of construction applicable to both arts and sciences was abandoned in the curriculum, and classes of application in fortifications, civil works, machines, and architecture were moved to the Engineering School of Metz; classes in chemistry and physics were submitted to the mathematics shock treatment. Laboratory work and graphic drawing classes were replaced systematically by theoretical classes in algebraic analysis. Thus, the Platonic-Augustinian method of constructive geometry and application that produced real scientists, was replaced by the Aristotelian-Jesuit approach of analytical memorizing, turning graduate students into singes savants.
 Figure 4. Carl Friedrich Gauss challenged the dogma of Cauchy et al., that all questions of science can he reduced to mathematical proofs. As Gauss insists, mathematics is the “queen” of the sciences, but physics is the “king.” |
The introduction of systematized mathematical analysis as the new basis for geometry, physics, and chemistry, by Laplace and Cauchy, is much more than an unfortunate mistake. Students are then ill-prepared for the necessary applications in practical fields.
The flaw went much deeper. Mathematical analysis was used, consciously, as an insidious form of virtual menticide, where students were mesmerized by tricksters into virtual reality, treated like morons, who were instilled with the fear of being called stupid, if they didn’t understand the formulas. When Cauchy stole Poinsot’s chair at the Ecole, one of his followers, J. Bertrand, admitted, “Only a few very gifted students could understand him [Cauchy]. This elite found him praiseworthy.”[16] From this standpoint, every discipline involving human creative knowledge had been subverted by being submitted to the test of linearization. The word was, “If you can’t mathematize it, it is not a valid discipline.” So, under the teaching of Cauchy, mathematics became the ultimate instrument of terror in making believe that mathematics could explain physical phenomena. For him, if nature could not fit into the mathematical equations, then nature was wrong, period.
So, at the Ecole, a discipline would be accredited in the hierarchy of sciences, only when mathematicians gave it their imprimatur; and the elitist’s choice of qualified students, for the entry examination, became decided, exclusively, on their ability to prove their competence in mathematics. It is from such a virtual reality principle that the artificial division between Arts and Sciences developed in the educational systems around the world. This corresponded to Karl Savigny’s separation between natural science (Naturwissenschaft) and art (Geisteswissenschaft). The remnants of this policy are found everywhere today, in our universities. And in the last ten years, the summum of this insanity has been discovered at the center of such acrobatics of the intellect as can be found in the mad financial derivatives bubble which is run by mathematical banking.
So, this whole business is a total fraud; accepted schoolbook mathematics is a fraud; the so-called “exact sciences” are a fraud; and their fraudulent nature lies in the formalism of underlying assumptions, whereby everything in the universe is educible to the perception of a perfectly continuous manifold, that is, defined by a single law, continuous in all directions, up, down, sideways, forward and backward, absolute, unchangeable, and perfectly objective, and where everything terminates at zero. Cauchy’s denial is that there cannot exist any true mathematical singularities. Everything converges smoothly, via infinite series, as well as smooth infinitesimals, while precluding the possibility of any real nonlinear discontinuities, in an otherwise objective-mechanistic world view. A good example of this is the case of the epistemological significance of the Cauchy notion of limit of functions, which actually represents a continuation and further extension of the attack on Leibniz’s calculus initiated by Euler in the eighteenth century.
The fictitious limits of bad infinitesimals
In the process of attempting to define linearly the notion of “limit of a function,” that is, what is, in practice, required for an engineer to calculate some variably decreasing function, or some area under a curve, a mathematician establish a method by which everything that is curvilinear is reduced to linearity. The thinking behind that is: “If you reduce straight lines (or numerical values) to a small enough size, the sum total of the tiny little lines will, sort of magically, become curvilinear, and the difference between straight and curved lines will become so small as to become zero.” This is how Cauchy, following in Euler’s footsteps, will define the limit of a variable quantity, or of analytical functions. “As the successive numerical values of the same variable decrease indefinitely, so as to become less than any preassigned given number, this variable becomes what is called an infinitesimal or an infinitely small quantity. A variable of this type has zero as limit.[17]
What Cauchy has just stated is that mathematical singularities, or discontinuities, do not exist. They can be flattened out and discarded as zeroes. Well, in point of fact, these incommensurable values, no matter how small they are, cannot be simply discarded. The following Figure 5 should serve as an example of the case in point.
Figure 5. Calculating the area under the curve.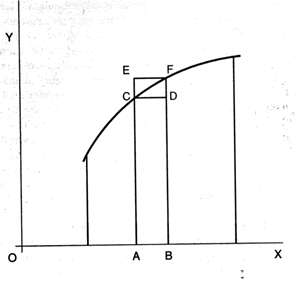 |
Consider Figure 5, a case of determining the limit of a function that will correspond to the area under this curve. [18] Take the area of rectangle ABCD: It is smaller than the surface ABCF. On the other hand, rectangle ABEF is a little larger. If you could find the perfect mean between the two, you would become the new Archimedes of modem times. But, you can determine only some approximation.
However, mathematics teachers don’t say that this is only an approximation. They claim that you can invent, out of thin air, a mental construct that will appear to solve the problem, and this is what Cauchy proceeds to do by flattening out the infinitesimals to zero. If you take the mean proportionality between the rectangles and then determine the sum of the mean rectangles as the equivalent for the area under the curve, you have cheated, purely and simply. You have reduced the reality of the human mind to linearity in the small. But, because you can couch this in a fancy formula like the definite integral of the function Y= f(x) between the values x = A and y = B, you are made to believe that, by repeating this procedure for each interval, the sum of the mean rectangles will give you the area under the curve.
This is very impressive, and it is made to appear acceptable as a replacement for the real physical area in question. In other words, you have been made to accept virtual reality as opposed to reality: You have accepted an approximation whereby you think you have achieved, analytically, the limit of a function when the number of rectangular intervals tends toward the equivalent of the area under the curve, but you have never actually reached that limit. You can only reach such a limit under very special synthetic conditions, like the case of the slave boy, in the Mena dialogue by Plato, where he discovers how to double the area of the square.
Ah! Such a discovery is actually generated through a jump function, a projection into the future, as a form of time reversal of causality which is totally opposite to Cauchy’s and Euler’s notion of percussive causality determined from the past. Thus, true discoveries are generated through a jump function, which belongs essentially to a time reversal function of man created in the image of God, that is, the very economic function that Lyndon LaRouche speaks of, which permits man to increase his own power of mastery over nature.
So, the difference is transinfinitesimal – not zero. Before the discovery, the slave boy is caught in infinitesimals; when he discovers the function of the diagonal, he discovers the discontinuity of the transinfinitesimal. That’s the jump function.
But, for Cauchy, this approach is unacceptable; therefore, the good Jesuit that he is, he needs a magician’s trick, whereby the discrepancies appear to be so small as to be negligible. So, abracadabra! “It is imperceptible; ergo it is acceptable.” That may satisfy the eyes of Cauchy’s students, but what about their minds? This is where a lot of damage has been done. This is a typical Cartesian argument, whereby Descartes concluded that because the movement of light is imperceptible, it must be instantaneous!
This fallacy of the limit of a function is a beautiful example of the fraud of accepted schoolbook mathematics. This is the fraud perpetrated by Newton, Descartes, Euler, Laplace, Lagrange, Cauchy, et al. which Nicolas of Cusa had exposed 400 years earlier, in developing a method of solving that type of problem. But Cauchy deliberately turned this fraud into a virtue, and by doing so, stopped scientific progress for countless generations. This principle of “virtuous limitation” is the paradigm of the rotten soul of French bureaucracy today.
By accepting this fallacy of composition, the mind is not only putting blinders on itself; it is accepting apparent limitations to its own creative development. On the other hand, if Cauchy had taken into account the breakthroughs of Cusa, he would have realized that the problem posed by the limits of a function is a clear case of the paradox of squaring the circle, and that the more you add to the number of singularities, the less you are approaching the non-linear nature of the curve. This means that straight lines and curved lines are two different species of geometric figures, and that the extension of the sides of a very large polygon, for example, could never make it become a circle.
But, instead of following this synthetic geometrical approach, Cauchy imposes the fallacy of Euler, as seen in their approach to analytical infinite series, convergent series, and power series, the so-called Lagrange series of celestial mechanics, and the like, which will continuously confirm the reductionist principle of so-called “mathematical rigor,” according to which the human mind is constrained by these fictitious limits of analytical functions.
Cauchy’s utilization of the Eulerian series-approach is not an arbitrary choice. Euler represents evil in science; morally, pure evil. Euler is the new Aristotle, as Pietro Pomponazzi was in his time: the man who destroys the soul, who denies the existence of creative mentation in the human mind. In this respect, Euler is the cornerstone of Immanuel Kant`s life’s work. Kant, who generated the chief framework of modem positivism, based his entire effort upon Euler, from his earliest attacks on Leibniz’s concept of Analysis Situs, to his late diatribes – “critiques” – against Leibniz’s “principle of sufficient reason,” or, even the possibility of the human creative mentation being knowable, let alone an efficient ontological cause.
Cauchy is quite conscious of his utilization of Euler, since his chief objective is to expunge all traces of Leibniz from the Ecole. As LaRouche details in his The Science of Christian Economy, Euler’s attack on Leibniz’s Monadology is the key to the degeneration of all modern mathematical physics into what is today represented as generally accepted classroom mathematical physics. Formally, Euler attacks Leibniz by simply asserting the primacy of the otherwise purely arbitrary assumption of naive Euclidean imagination: Linear extension is perfectly continuous without limit. But Euler’s supposed proof of that assertion depends absolutely upon the assertion of that axiom which it purports to prove. Therefore, Euler’s famous tautology proves nothing at all. And in this regard, Euler’s folly on this point is the hereditary origin, via Lagrange and Laplace, of Cauchy’s bowdlerization of Leibniz’s version of a calculus. And, as seen in the above case, with Cauchy’s application of Euler’s method, these limits are again truly nothing but fallacies of composition, limits of mathemagics, which will lead the mind to intellectual sclerosis, creative paralysis and, ultimately, to menticide.
Yet one might still ask: “But why would you want to destroy such a beautiful education program as that of Carnot and Monge'?” Well, if we let the defendant speak for himself, we shall have the answer. Let us hear what Cauchy has to say, and see how he expresses, in his own words, the kind of “cultural optimism” that he believed in. The following statement tells to what degree Cauchy believed in the powers of creativity, and what importance he gave to human discovery:
“When we take a quick look at the productions of the human mind, we are tempted to believe that human knowledge can grow and multiply at infinity .... However, if we observe that all of our intelligence and our means are enclosed within limits that can never be superseded, we will persuade ourselves that our knowledge is limited …. that if man has been unable to visit the poles, he remains in an eternal despair of ever reaching these frozen regions .... Who will ever be able to dig a well of 1,500 leagues deep? We have managed to elevate ourselves to 1,500 fathoms in the atmosphere, but the rarity of the air . . . will constantly bring back to earth`s surface whoever would want to reach higher .... Exact sciences can be considered as completed sciences. ... By means of sophisms man can come to the point of doubting these truths we teach him, but he will never discover new ones!" (Cauchy, Cherbourg, 1811)
Ultimately, this testament to the state of his own mind reveals his deep-seated hatred for scientific and technological progress, the hatred of what makes a human being creative, in the image of God, and thus makes him the undisputed master of the universe. This is what Cauchy hated the most: that which increases man’s power over nature. It is for that reason, because of his mediocrity, that he was chosen by Pozzo, and his masters, to destroy the Ecole Polytechnique. Indeed, the point should be made, that it was not for his qualities of genius that Cauchy was chosen to take control of the Ecole; but exactly for opposite reasons, that is, because of his shortcomings, his closed-mindedness, and his oligarchical fanaticism. By the time Cauchy was expelled from the Ecole Polytechnique, in 1830, and was forced out of France into exile with his Bourbon King, the damage was so extensive, that what was left of the school was but a ghostly shadow of its former greatness.
Auguste Comte: the cult of positivism
But, just as you think that the Ecole has received its lowest blow, in comes Auguste Comte and his positivist perversion. Comte (1798-1857) is an oligarchical lackey of Count Henri de Saint-Simon, a socialist-positivist, Venetian type, who promoted the reorganization of European society based on so-called “human science." As a student, and later, as a teacher at the Ecole Polytechnique, roughly from 1814 to 1844, Comte poses as a redresser of wrongs, and combats the Ecole for the excesses and abuses of algebraic analysis. In doing so, he proposes a more extreme remedy in exchange. The proposed cure, positivism, will be much worse than the disease.
During the 1840 period, Comte proposed to replace the general education system of the Ecole Polytechnique based on the deductive method of algebraic analysis, with a new system based on the inductive method of a so-called “positivist philosophy,” which is nothing else but the introduction of a rationalization for an encyclopedic knowledge claiming to “replace the analytical tendency by a synthetic tendency.”[19]
Auguste Comte was calling for a total reform of the educational system, including the exclusion of particular formations related to applications in trades, exclusion of technical studies, and recruitment of students based on extremely selective criteria, according to the new religion of man without God which was to “form the core of a true contemplative class.”[20] After a brutal fight at the school between students and teachers, the school authorities decided to repudiate Comte, who was removed from his teaching functions, in I844. Among other foul ideas that Comte introduced at the school, was the proposed replacement of the notion of Christian Trinity of “Father, Son, and Holy Spirit” by the feminism trinity cult of “Mother, Wife, Daughter.”
Thus, the elevated mission of the Ecole Polytechnique was sabotaged perverted, and destroyed by Laplace, Cauchy, and Comte, and had to be pursued outside of France, particularly at Gottingen University in Germany, where the Humboldt brothers, Gauss, Riemann, Weber, and others would continue the tradition of Carnot and Monge.
Pasteur on reviving enthusiasm: the ‘inner God’
 Figure 6. Louis Pasteur (1822-1895) by Karel Veireycken, 1986. “The positivist conception of the world does not take into account the most important positive notion – that of the infinite.” |
Before the Tribunal of Reason, the Ecole Polytechnique stands as a towering beacon of hope and generosity, a great gift to all of mankind; and it is our task, today, to make sure that such a heritage comes alive again, in the hearts and minds of all young men and women of good will. So many great scientists, like Louis Pasteur, inspired by the enthusiasm of Carnot and Monge, and their Platonic heritage, were passionate lovers of ideas; each and every one of them lived, fought and died for the sake of communicating such Platonic ideas to future generations. Thus, the following beautiful statement of Pasteur against the positivisms of Cauchy and Comte, while recalling his commitment to the high purpose of enthusiasm in the Ecole Polytechnique and in the Academy of Sciences, in 1882:
"Positivism sins not only through methodological error. There is a considerable gap in its seemingly tight net of reasoning .... The large and obvious flaw in the system consists in that the positivist conception of the world does not take into account the most important of positive notions-that of the infinite.
"What lies beyond the starry vault of the heavens? More starry heavens. So be it! And beyond? Pushed by an invisible force, the human mind will never cease asking itself: What is there beyond? Does it want to stop either in time or space? Since an endpoint would be merely a finite dimension, greater only than those that had preceded it, no sooner does the mind begin to envision it than this implacable question returns, and the mind cannot quell curiosity`s call .... Positivism gratuitously brushes aside this positive and fundamental notion, along with its consequences for the life of society ....
"Are not the science and passion of understanding nothing else but the effects of the spur of knowledge. put in our souls by the mystery of the universe? Where are the real sources of human dignity, of liberty, and of modem democracy, if not in the notion of the infinite before which all men are equal?
"The spiritual bond situated [by the positivists – ed.] within a sort of lower-level religion of Man cannot reside elsewhere than within the higher notion of the infinite, because this spiritual bond must be associated with the mystery of the world. The Religion of Man is one of those superficially obvious and suspect ideas which brought one eminent psychologist to say: ‘l have thought for a long time that the person who has only clear and precise ideas must assuredly be a fool. For the most precious notions harbored by human intelligence are deeply behind-the-scene and in semi-daylight, and it is around these confused ideas, whose interrelations escape us, that the clear ideas gravitate extending, developing, and germinating themselves.` If we were cut off from this background the exact sciences would lose the greatness which they draw from the secret rapport they hold with those infinite truths whose existence we can only suspect.
"The Greeks understood this mysterious power below the surface of things. It is they who bequeathed to us one of the most beautiful words of our language: the word enthusiasm, [which means] inner God.
“The greatness of human actions is measured by the inspiration that gives them birth, joyous is he who carries within him an inner God, an ideal of beauty, which he obeys: an ideal of art, an ideal of science, an ideal of his nation, an ideal of the virtues of the Gospel. These are the living sources of great thoughts and great actions, and all of them are lit by the gleam of the infinite." [21]
_______________________________________________________________________________
1. The author wishes to thank Charles Stevens for his precious collaboration, especially for his well-researched section on “Laplace, the Newton of France.” For an extensive review of the positive role played by the Ecole Polytechnique, see Jacques Cheminade, Regard sur la France républicaine (Paris: Editions Alcuin, 1991); Claude Albert, “The Ecole Polytechnique and the Science of Republican Education,” The Campaigner, July 1980; Pierre Beaudry, “The Metaphor of Perspective,” Fidelio, Summer 1995; Dino de Paoli, “Lazare Carnot’s Grand Strategy for Political Victory,” EIR, Sept. 20, 1996.
2. Jacques Cheminade, “Time to Destroy the Mythology of Bonapartism,” EIR, Oct; 18, 1996.
3. Lazare Carnot, from the “Drawing Section of the Public Works Curriculum,” Ecole Polytechnique, 1794. On the notions of “ideal perspective” and “sentiment” see Beaudry, op. cit., Fidelio, Summer 1995. The French use of “sentiment” relates to higher emotions, rather than to “feelings” or “sentimentality” as the term usually connotes in English. The sentiment of enthusiasm, for Carnot, corresponds to such an emotion as agape, which he will generally associate with Platonic Ideas, like love of justice, love of country, love of mankind, relating to the universal ideals of common good, as opposed to “personal” interests. For “aerial perspective” in Leonardo da Vinci, see also Karel Vereycken, “The Invention of Perspective,” Fidelio, Winter 1996. The reader can find a complement of this Carnot Machine-Tool Principle in Lyndon H. LaRouche, Jr., “Return to the Machine-Tool principle,” EIR, Feb. 7, 1997.
4. Bruno Belhoste, Augustin-Louis Cauchy, A Biography (New York: Springer-Verlag, 1991), pp. 45-46.
5. C. A. Valson, La vie et les travaux du Baron Cauchy, 2 vols. (Paris, 1868).
6. See Felix Klein, "Development of` Mathematics in the 19th Century" (English translation in Math Science, 1979); E.T. Bell, Men ty`Matl1entatic's (New York: Simon & Schuster, I937); Jesper Luetzen, Joseph Liouville 1809-1882 ,° Master if Pure and Applied Mathematics (New York: Springer-Verlag, 1988); Michael Monastyrsky, Riemann, Topology, and Pure Ph. vst't°s (Birkhauser, 1987); John Maynard Keynes, “Newton the Man" read at the Newton Tercentenary Celebrations. Trinity College. Cambridge. on July l7, 1946; Sir David Brewster, "Life and Style of Isaac Newton."
7. Cauchy did not limit his evil to suppression and plagiarism. Cauchy contributed, at least, to the impoverishment of Abel which led to the latter`s early death, and Galois was probably assassinated by a Bourbon police agent. See Leopold lnfeld, Whom the Gods Love: The Story Evariste Galois (Reston, Virginia: National Council of Teachers of Mathematics), Alexandre Dumas, Mes Mémoires, l863-65.
8. .Jean-Victor Poncelet Propriétés projectives des figures. Paris. See also. Poncelet, Applications d’Analyse el de Géométrie. vol. 2 (Paris, I 864), p.564.
9. Belhoste, Op. Cit.,. p. 46.
10. Lyndon H. LaRouche, Jr., "The Essential Role of ‘Time-Reversal’ in Mathematical Economics." EIR, Oct. 11, I996.
11. Lyndon H. LaRouche. Jr.. "The Principle of Curvature in Politics," verbal briefing to EIR staff. Leesburg, Virginia, Oct. l9. I996. See also LaRouche, The Science of Christian Economy (Washington. D.C.: Schiller Institute, 1991). Appendix Xl, "Euler's Fallacies on the Subject of Infinite Divisibility and Leibniz's Monads," pp. 407-425.
12. Jean-Victor Poncelet. Polémiques et fragments divers.
13. Belhoste, op. cit., p. 68. Bell, op. cit., p. 292.
14. Laurence Hecht. “The Atomic Science Textbooks Don’t Teach: The Significance of the 1845 Gauss-Weber Correspondence," 21st Century Science & Technology, Fall 1996. See also Dr. Rémi Saumont, “The Battle Over the Laws of Electrodynamics," 21st Century Science & Technology, Spring 1997.
15. The general historical background for this is to be found in Anton Chaitkin. “The ‘Land-Bridge? Henry Carey’s Global Development Program," EIR, May 2, 1997.
16. J. Bertrand, “Notice sur Louis Poinsot," in L. Poinsot, Eléments de Statique (Paris, 1873).
17. Belhoste. Op. Cit.. p. 74.
18. E. Kasner and J. Newman, Les mathématiques et l’imagination (Paris: Payot). p. 230.
19. Belhoste, Dalmedico, and Picon, La formation polytechnicienne, 1794-1994 (Paris: Dunod, 1994).
20. Auguste Comte, Systéme de politique positive, Vol. 1, Paris. pp. 170-190. Quoted by Annie Petit in Belhoste, Dalmedico, and Picon, Op. Cit., p. 66.
21. Louis Pasteur, speech delivered at the French Academy of Sciences, 1882.
Related pages:
