
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps
Dialogue of Cultures
Spaceless-Timeless Boundries
in Leibniz
by
Lyndon H. LaRouche, Jr.
July 2, 1997
For related articles, scroll down or click here.
This article is reprinted from the Fall 1997 issue of FIDELIO Magazine.
Eratosthenes' Estimate for the Spheroid
Machine Tool Principle: The Brains of Profit
Fidelio, Vol. VI ,No, 3. Fall 1997
Spaceless-Timeless Boundaries in Leibniz
by
Lyndon H. LaRouche, Jr.
July 2, 1997
| We know we exist within the universe, when we begin to change that universe for the better, when we begin to realize the inborn, special potential of the human individual, the cognition whose power to make miracles fascinated our Johnny and Jimmy. Somewhere, in the higher reaches of hypothesizing the higher hypotheses, mankind is known to exist as the kind of special creature whose innermost nature, whose outermost efficiency, Johnny and Jimmy were exploring in the classroom. Man exists because man is needed. |
|||
I think that the parade of ideas represented by de Paoli's manuscript, is, by itself, fully adequate for the specific line of argument he develops there. Therefore, I concluded that the appropriate place for my added points of emphasis, would be an epilogue to his work.
As de Paoli touches repeatedly upon this point in his paper, the first known notion of a self-bounded domain, appears in the work of Plato.2 After Plato, that conception finds a central position in writings of St. Augustine,3 is the center of work founding modern experimental physics, Nicolaus of Cusa's De docta ignorantia, is the kernel of Johannes Kepler's method for determining the solar orbits, and, is the heart of the method of Gottfried Leibniz. It is the central feature of Bernhard Riemann's revolutionary, 1854 habilitation dissertation, and spills over, from there, into Albert Einstein's notion of relativity. It is the central feature of all those portions of my own work, in which I address the subjects of cognition, evolution, and the physical-economic notion of “anti-entropy.”
This conception of the bounded domain, acquired its most rigorous expression in Plato's later writings. This leading feature of all those dialogues, appears by way of the central ontological paradox—the One-Many paradox—introduced in his Parmenides.4 That dialogue was a central point of reference for Gottfried Leibniz. It is the point of departure for addressing the subject of self-bounded domains, here.
Boundedness: The Case
of Simple Hypothesis
Given, a series of transformations in sundry kinds of objects, which is more real, the individual objects of that series, or the underlying process of transformation which orders the changes involved? What is the One underlying principle of change, which, in this way, subsumes the Many elements within that series? de Paoli's paper makes repeated references to the appearance of this Platonic conception in the work of Leibniz.
The solution to that Parmenides paradox is the indispensable precondition for comprehension of any intrinsically non-linear process, such as distinguishing, functionally, between living and non-living processes, and between the mental processes of men and monkeys. On this account, the implications of the Parmenides paradox occupy a central position in all of my references to the scientific principles on which competent economic studies depend absolutely. Since 1952, my most frequent references to this Platonic principle, have been keyed to the form in which that is presented in Bernhard Riemann's 1854 habilitation dissertation, the paper which founded the first true non-Euclidean geometry.5 For the purposes implicit in de Paoli's paper, the best choice of my recent treatments of this matter, is my “The Essential Role of 'Time-Reversal' in Mathematical Economics.”6
That much said as a matter of required introduction, we now proceed to construct the relevant argument underlying the notion of self-bounded domains.
In any rational system of thought, such as the geometry of Euclid, Socratic method shows, that the possibility of consistency among those propositions which we treat as theorems, depends upon a discoverable set of axiomatic assumptions, such as adducible definitions, axioms, and postulates. The Classical term identifying such a set, is “hypothesis.” The set of definitions, axioms, and postulates associated with a Euclidean geometry, is to be recognized as a case of simple hypothesis.
The collection of theorems associated with such underlying assumptions, is usefully described as a “theorem-lattice.” Once such a simple hypothesis, such as a Euclidean one, is adopted, the standard which a proposition must meet, to qualify as a member of that lattice, is that it must not contradict the existence of any among the set of definitions, axioms, and postulates of the relevant hypothesis.
That theorem-lattice, so bounded, and subsumed, by its hypothesis, constitutes a simply bounded domain. If the hypothesis itself could be included within that array, the result would represent a self-bounded domain. For reasons which de Paoli references in his published work on the relevant discoveries of Georg Cantor and Kurt Gödel, no formal, deductive-inductive system, such as a Euclidean geometry, could satisfy the requirements of a self-bounded domain.7 Nonetheless, the relations between the theorem-lattice and hypothesis, even as they appear in a deductive-inductive domain, are worth examining, as a preparatory step toward comprehension of actually self-bounded domains.
Anyone who recalls the experience of a “pre-New-Math” education in Classical Euclidean geometry, could reflect on the fact, that the pedagogically efficient chain of lesson-plans ordering the theorems of that curriculum, form a sequence. Extension through any orderable sequence, connotes the functional notion of relative time. The working point here, is that, although the theorems may be thus orderable in relative time, the hypothesis which underlies the generation of those theorems, does not change from the first to last element of that pedagogical sequence: the hypothesis has the quality of relative timelessness; that hypothesis exists simultaneously in all times and places which might be occupied by the occurrence of any present or future theorem of the corresponding theorem-lattice. Thus, because of this consideration (simultaneity), and, also, of the notion of hypothesis as “efficiently underlying” the whole existence of the theorem-lattice, the relatively timeless hypothesis “bounds” the entirety of the virtual space-time domain coincident with that lattice.
I imagine the commonplace expression in today's U.S.A., would be: “Switch channels for just a moment.” de Paoli referenced, repeatedly, passages in Leibniz's writings in which Leibniz was expressing an application of Plato's Parmenides conception; and, sometimes, also, the Classical Christian conception of God as dwelling within His universe (not outside it). However, God dwells not within the confines (“bounds”) of time and space, but, rather, exists pervasively in “the universal simultaneity of eternity” of His entire Creation. That is the kind of conception toward which we are working our way, step by step, here. The “relative timelessness” of even simple Socratic hypothesis, already contains the germ of the conception which Leibniz knew as “simultaneity of eternity.”8
Now, that said, back to where we left off before this interpolation. Move ahead, from the case of simple hypothesis, to higher hypothesis. Focus upon the case of Bernhard Riemann's revolutionary discovery: a generalized notion of physical geometry.
How The Human Mind Actually Functions:
Higher Hypothesis
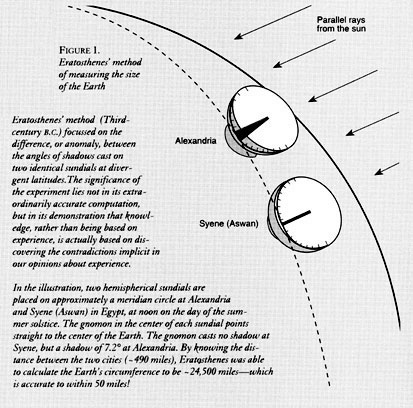
Imagine that you are the most celebrated fellow-scientist among Archimedes' contemporaries and colleagues, the mathematician Eratosthenes, from Plato's Academy at Athens. Eratosthenes was, during the time of his correspondence with Archimedes, the leading scientific mind of Egypt. Among Eratosthenes' numerous other revolutionary discoveries of universal principle, he conducted an experiment which not only proved that the Earth was approximately spherical—not flat, but also gave him a remarkably good estimate for the size of the Earth.9 In fact, this discovery in the field of geodesy, during the Third century BCE , made possible the construction, about seventeen centuries later, of the world map drawn by Nicolaus of Cusa's associate Paolo Toscanelli. The latter was the same map which Columbus used to plan his first, 1492, voyage of discovery to the Caribbean.10 The specific importance of that discovery by Eratosthenes, for our purposes here, is that it contains within it the germ of the essential principles common to all valid fundamental, experimental discoveries of universal physical principles. That is the principle, as developed by Carl F. Gauss, upon which Riemann based his revolution in physics; we reference that experiment here to illustrate Riemann's principle.
“Is the Earth flat?” That is to say, if a plumb-bob on a string points downward, could we construct, at a level below any part of the Earth's water-level surface, a plane which would always intersect, at right angles, all of the lines extended from all plumb-bobs? If so, then, we could also construct a plane just sufficiently above any local region of the Earth's ground/water surface, that it would always be at approximately right angles with all plumb-bob lines, and yet never more than merely touch the surface of earth or waters, tangentially, in that locality. Choose a region along the Nile from Aswan to Alexandria. Select the direction of this line to correspond to an astrophysically-determined south-north direction. Define noon, as the instant the shadow cast a by an upright pin (as aligned by a plumb-bob) lies along that south-north line. Now, as the sun appears to move from east to west, consider the area swept by the shadow of the pin upon a surface which always lies at a right angle to the plumb-bob lines. This shadow will define the relevant sector of a circle. The plane of that sector, then, defines the supposed “flat Earth.”
Measure the distance from Aswan to Alexandria along the south-north line.
| Figure I |
|||||
 |
|||||
| go back to appended remarks |
|||||
Now, compare the marked angles defined, simultaneously, by the shadows of the pins of each and all of the sundials. The angles are different; the difference is ordered, south-north, by a consistent difference of “more than” that shadow cast by the preceding sundial. If the sun were a large object, located at a great distance from a presumed “flat” Earth, the angles ought to appear no worse than very nearly equal, according to the proposition expressed by the design of the experiment. Express copies of each and all among these angles, as sectors of a circle. Shade-in the sector of that circle defined as the difference between the smallest and largest of these angles. Note the length of the arc of the circle defined by that shaded area of difference. Now, that latter arc corresponds to idea of the distance between the relatively most southerly, and relatively most northerly placements of the sundials.
By the principle of similar figures, the Earth is shown to be a spheroid, and the length of the approximate Great Circle, defined by the experiment's south-north direction, can be estimated by treating the arc in question as an arc of that Great Circle. Eratosthenes' estimate for the polar diameter of a spheroid-Earth, was off by a margin of about fifty miles.11
The purpose of supplying this description, here, is to demonstrate, that in the scientific method developed by Plato, and also such among his collaborators as Theaetetus and Eudoxus, there is contained the germ of the same principle upon which Nicolaus of Cusa based the launching of the modern experimental physics of his followers Leonardo da Vinci, Johannes Kepler, Gottfried Leibniz, et al., the same principle at the foundation of Carl Gauss' discoveries in astrophysics, geodesy, and geomagnetism, the same principle of experimental physics expressed by Gauss' development of the theory of curved surfaces out of his work on biquadratic residues, all this the work of Gauss upon which Bernhard Riemann premised the discovery of the first true non-Euclidean (e.g., physical) geometry.12
Look again at Eratosthenes' experiment, from this modern vantage-point.
As we indicated, the design of the experiment conformed to testing the “flat Earth” assumption. In other words, an assumption that the subject of the experiment lay within a two-dimensional phase-space. The evidence showed a deviation from simply linear extension, requiring the introduction of a third dimension, a three-dimensional phase-space. As Nicolaus of Cusa showed the transcendental nature of pi (&Mac185;), in demonstrating that the sides of a many-sided regular polygon could never coincide with the circumference of the circle inscribing it,13 the fact that the Earth's surfaced is curved, not flat, shows that at every smallest infinitesimal interval along any attempted linear extension of the tangent to that surface, the two dimensions of the tangential plane are rendered discontinuous (i.e., “non-linear”) by the causally efficient, “bending” presence of the third dimension. This feature of Eratosthenes' experiment, becomes crucial in that work leading through Gauss' contributions into Riemann's employment of Leibniz's principle of Analysis Situs, to generate the discovery of the first true, “non-linear,” physical geometry.
Now, focus sharply upon the question: “What is the kernel of this experimental method?” That kernel is, that all validatable discoveries of a new physical principle, are each derived as the generation of original conceptions which resolve an experimental paradox of the following general specifications.
In each case, as in the referenced case of Eratosthenes' experiment, we approach the experimental subject-matter burdened with the freight of our preestablished opinion: at best, with a well-grounded hypothesis, as we have defined the notion of simple hypothesis above. However, we have added something else. In the first type of instance, we confront our preestablished mind-set with a fact which is as believable, by its nature, and by the same methods of observation which we have employed to support our preexisting hypothesis. We are able to show, and that in a fashion to which our preestablished beliefs could not object, that the disturbing fact has the same kind of experimental authority as we have supposed our preestablished hypothesis had had up to this time. However, the efficient existence of the new fact introduced, can not be accepted as a valid theorem of the preestablished hypothesis. Thus, these two, equally validated sets of facts, can not co-exist in the virtual universe which we had believed we inhabited. A true paradox.
Plato's Parmenides is exemplary. Do the terms of the series exist? “Without doubt.” Does the difference among the terms of the series exist? “Also, without doubt.” Do these two kinds of facts inhabit the same universe? “It can not be denied.” Then, the commonality of the terms of the series, is the adducible commonality of their differences? “Yes” (perhaps, one hears a tone of reluctance). Then, that commonality exists? Silence: paradox. Then, that commonality subsumes the co-existence of the terms and their differences? Stunned silence: once again, by means of ontological paradox, we are compelled to cross over from the virtual reality of mathematical formalism, into Riemann's “domain of physics,” science.14
Confronted with such paradoxes, successful original discoverers have generated ideas which prove to be solutions. If we are able to validate these ideas experimentally, we call these ideas “new physical principles.” The problem is, that although we are able to prove the existence of the discovered principle by experimental methods, we can not represent explicitly, in mathematics, or in any other medium of communication, the mental processes, entirely within the individual mind, by means of which such valid ideas are generated. This process of discovery, entirely within the sovereign recesses of the individual discoverer's cognitive processes, can not be degraded for representation, into a form of analysis which could be explicitly represented within the bounds of words or mathematical procedures.
We can represent the object, the discovery, produced, as it may be explicitly presented as an experimentally validated solution for the explicitly stated relevant paradox; but, we can not satisfy the demands of the smelly street-beggars of formal logic and sense-certainty, to produce a representation of cognition which is agreeable to their prejudices. The fact that these ideas can not be explicitly represented in such ways, misleads such misguided persons, who are sometimes known as empiricists, positivists, or sophists, into arguing, that this difficulty signifies something defective in this class of ideas. “Perhaps,” they argue, “these kinds of ideas are only airy, mystical fantasies.”
Such critics behave very foolishly. Unlike the empiricists, really intelligent people know these kinds of ideas far better, with far greater scientific certainty than anyone could know sense-impressions as such. The proof of that latter fact, is readily demonstrated to intelligent, competently educated school-children. This statement is to be recognized as representing a paradox about paradoxes and their solutions.
This extraordinarily relevant, and most important paradox, must be restated here, once more. That act of discovery, which proves experimentally to have been a valid, original discovery of a new physical principle, occurs entirely within the sovereign domain of the individual person's cognitive processes. The production of such ideas could never be analyzed in the way a manufacturing design is analyzed into the form of a division of assembly-line labor in a manufacturing firm. The sophist might be tempted to interject: “See, you admit that you do not know what was going on in the mind of the person who made that discovery!” False! Some among us do know.
Really intelligent people, do know. How do we know this? We can repeat the discovery within our own sovereign cognitive processes; intelligent primary- and secondary-school pupils do this often. This is what is commonly called “a good education.” In a good educational program, the pupils are aided in reliving the act of each among a series of those original discoveries of principle, the which have been passed down to us from persons who often lived centuries, or even millenia earlier.
“How?” We confront the pupil with the facts of the paradox which confronted that discoverer. We structure the curriculum to bring each such challenge to the pupil, at the point in the curriculum that that student has accumulated the prerequisites for tackling the problem. We structure the social situation, to foster a positively catalytic, relevant quality of Socratic interaction among the members of the class (teacher and pupils). We do not “tell” the pupils the answer, until they, or, at least, some among them, have made the relevant break-through. We, then, assist the pupils in discovering how the discovery may be experimentally validated. We, then, walk the class, as a whole, through the Socratic process of reexamining each step of the preceding process, from paradox through to experimental validation.
In an educational process of that sort, the subject being taught is “the experimental scientific method.” Yes, we are also fostering the pupil's reenactment of particular discoveries of principle, in his or her own mind. Those are the individual terms of a process of education, but not the educational process itself. Our familiar friend, the ontological paradox of Plato's Parmenides, has, once again, put in its appearance. The individual topics addressed in the successive lesson-plans, are the individual terms of the sequence of education, the Many. The corresponding One, the real subject of the course considered as a whole, is the Socratic method for generating valid new discoveries of principle. That One is the educational process, within which these Many are making their functionally ordered appearance, manifesting the differences among all of them, each in turn.15
If we are successful, we are invoking two classes of conceptions within each individual student.
First, on the relatively lower level, the student is being enabled to watch the cognitive processes which are in play, during the successful generation of a new idea which solves an ontological paradox of the type indicated here. Although we can not look directly, by means of our senses, into the sovereign cognitive processes of another person's mind, that person has the potential ability to look into his, or her own cognitive processes.
The success of this attempt, to know oneself, as Socrates prescribes, depends, more or less absolutely, upon a second class of conceptions. This second class focusses upon the social process within which individuals' cognitive processes of discovery are situated.
Teacher: “How did Johnny discover the solution? Jimmy, do you wish to take a stab at it?”
Jimmy: (Smiling proudly) “Sure. He had to be thinking the same thing I was thinking. ...”
Johnny, at that point, may be thinking, that if Jimmy can look into Johnny's mind, perhaps, Johnny, by thinking about that, can see into his own mind. In other words, if Johnny can construct a kind of clone-image of Jimmy, within his own, sovereign domain of cognition, that “clone-Jimmy” would be situated to watch Johnny's cognitive processes at work. In that way, Johnny could be looking over clone-Jimmy's cognitive shoulder, at Johnny's own cognitive-processes-at-work. That is the “secret” of the Socratic method's superiority to any other mode of thinking. The essential function of the schoolroom class, is to produce that optimistic quality of Socratic interaction among the pupils, the which is the most likely method for producing the relatively maximum ration of such geniuses.
We can not look directly into the cognitive processes of other persons. There is no “objective” method, through the senses, or through a medium of language, to see directly the cognitive processes operating within the mind of another person. Nor, for that matter, has any scientist ever seen directly the domain of nuclear microphysics. However, we have three “objective facts” respecting any validated discovery of new physical principle (for example), by aid of which we can know how the mind of another person, even one long deceased, produced that validated idea. These three facts are: the paradox, which demanded the solution; the reflection, in the form of an instruction, of the discovered idea, which represents the discovered solution for that paradox; and, the experimental validation of the efficient existence of the discovered idea of the new physical principle. If any among us has replicated the generation of that solution from our own cognitive processes' successful replication of the original discoverer's attack upon the paradox, that internal cognitive experience by each among us, represents shared, validated knowledge of the generated idea.
“Look at your mind, Jimmy. What is the real reason you said that? Look behind what you were thinking, then. Was there some assumption, which caused you to choose that answer?” The same principle, by means of which a class of pupils may find the excitement of being able to “see directly” into their own and other pupil's minds, by aid of the kind social interaction just described, is the key to the Socratic method of looking at one's own sovereign processes of cognition, in an efficiently critical way.
On that account, the opening two paragraphs of Riemann's habilitation dissertation, are the most important part of that entire work: they state the paradox which the dissertation, in its entirety, is deployed to solve.
There, first, Riemann instructs us to recognize (as Leibniz had already warned us of this), that the whole business of a mathematics derived from using Euclid's geometry as a basis for algebra, is flawed, from the outset, with incurably mystical, and, in fact, false presumptions. Second, that, up to that time, the most famous mathematicians and philosophers, from Euclid through the great A.-M. Legendre, had failed to pierce this veil of darkness.16 Third, that Riemann himself will proceed, after those two paragraphs, to lift that veil, inch by inch, and, so, present a new conception of mathematics, from the standpoint of experimental physics.
In the Platonic way of thinking which Riemann's discovery expresses, as did Leibniz before him, the idea of space and time as Kantian absolutes, is banned from science. Each of the two is reduced from the aprioristic rank of mathematical royalty, to the that of just another participating, colligating citizen, like mass, of the n-dimensional republic of experimental physics.
As is adequately elaborated in sources such as my above-cited paper,17 in Riemannian “non-Euclidean,” or “physical” geometry, every permitted extensible dimension of that geometry, is derived from an experimentally validated discovery of universal principle. Paradigmatically, we associate this notion, of a physical, or non-Euclidean geometry, with so-called “physical principles.” However, since the efficient existence of mankind, and the sovereign cognitive processes of discovery of principle itself, are integral features of a self-bounded universal domain, this universe, we must, as de Paoli has emphasized the necessity for this, and as Riemann also recognized this,18 include the discovered characteristics of cognition itself as “principles of nature.”
So, Riemann strips the idea of “space” and “time,” as supposed geometric dimensions, of their claims to a priori existence within geometry. Aprioristic presumption is to be replaced, entirely, by relativistic notions of space and time, each of these premised upon nothing other, and nothing more than, the experimental standard of proof for physical principles. The false, incompetent, contemplative view, which is proposed by an Aristotle and Averroes, as by the materialists, the empiricists, the positivists, and the existentialists generally, is prohibited from future intrusions upon the domain of scientific Reason.
At this point, the science of physical economy takes over.
The empirical foundation of physical economy, is the progress of mankind, as expressed in a positive correlation between increased potential relative population-density, and improvement of demographic characteristics of the households of that population taken in its entirety.19 [see: Figure 2 and Table I] The outstanding, and indispensable feature of such progress, is scientific and technological progress; however, the principles of Classical artistic culture have indispensable bearing upon the ability of a population to assimilate, and to generate the benefits of scientific and technological progress. For our immediate purposes, let it be understood that what we say respecting scientific progress is merely exemplary of the combined effect of advances in knowledge in both physical science in Classical art-forms. The science of physical economy is rooted in the study of the reciprocal relationship between advances in knowledge of principle effected through the cognitive processes of the individual mind, and how the ordering of the practice of the same society fosters, or injures, the reproduction and further improvements in power of those sovereign cognitive processes within the individual members of society.
The correlation and connection between the two facets of that cognitive process, its inputs and outputs, so to speak, and the increase of “anti-entropy” of the physical-economic process, is the proper center of attention, in efforts to define relevant notions of functional relationship between mankind and the universe at large.
We now examine, summarily, the minimal relevant essentials of that science.
The general principle which I have employed, since late 1952, to represent the impulse of scientific and technological progress, is the notion, that the number of dimensions of a Riemannian manifold is (implicitly) the number of validated discoveries of principle cumulatively represented by the relevant human practice. Each new, validated discovery of principle, thus, effects a transformation denoted by the ordering, n to n+1. That taken into account, we have the following.
My first general contribution to advancement of Leibniz's science of physical economy, was the notion of “anti-entropy” as expressed by physical economy itself. Expressed in descriptive terms, we have the following. Let the amount of physical-economic investment per capita, required to maintain equi-potential of the demographically expressed potential relative population-density of the economic process, be regarded as the per-capita “energy of the system.” Let physical-economic output in excess of required “energy of the system,” be regarded as “free energy.” Then, under the condition that the per-capita physical-economic costs of the per-capita “energy of the system” increase as a function of technological progress, the ratio of “free energy” to “energy of the system” must not decline, and must, preferably increase through technology-driven, capital-intensive, power-intensive modes of increase of the productive powers of labor. This expresses “anti-entropy” of the productive process as such.
My second general contribution, involves the use of the mathematical notion of “cardinality” to express the quality of transformation which occurs through increasing the implicitly denumerable density of mathematical discontinuities per arbitrarily chosen interval of action. This, I correlate with the increase of a Riemannian manifold, from one of “n dimensions,” to a higher order of “n+1 dimensions.” This is another way of expressing the dimensionality of the manifold.
Thus, the increase in “cardinality,” so defined, represented by a succession of scientific and technological advances of the form n → n+1, is an anti-entropic impulse. The realization of that impulse, in the mode of capital-intensive, power-intensive progress, generates that increase of the ratio of “free energy” to “energy of the system,” the which expresses the anti-entropic, physical-economic determination of an increase of the potential relative population-density of the society.
Thus, the impulse of scientific and technological progress corresponds to an ascending series of manifolds, n, n+1, n+2, ... . Since each such manifold is bounded by an hypothesis, the which is absolutely inconsistent with the hypotheses corresponding to all other manifolds of the series, we have a new form of the Parmenides paradox, in which the individual terms are simple hypotheses of the Riemannian-manifold form. The difference among these manifolds (hypotheses) defines a subsuming hypothesis, corresponding to Plato's notion of “higher hypothesis.” This “higher hypothesis” expresses that principle of cognition, through which the relevant, validated new discoveries of principle have been generated.
That, in essence, is the kernel of the LaRouche-Riemann Method, so called, because it is the application of Riemann's discoveries to the problems of measurement posed by my own definitions of both physical-economic anti-entropy, and of cognition.
This notion of higher hypothesis, so situated, defines the economic-demographic process as a bounded domain. The higher hypothesis, otherwise to be recognized as the principle of cognitive, successive generation of validated, paradox-driven, new discoveries of principle, is timeless relative to the sequence represented by the series of physical-economically realized manifolds.
The Parmenides type of paradox so posed, is resolved by the discovery of this higher hypothesis through the processes of cognition. This discovery represents simply a higher order of the same kind of discovery realized as validated simple hypothesis.
This higher hypothesis is itself subject to improvement. Think of a series of higher hypotheses, as a representation of the process of improvement. Name that series “hypothesizing the higher hypothesis.” The latter is only a higher order of the principle of discovery associated with the generation of an higher hypothesis.
Each of these higher hypotheses is relatively timeless—relative to the series of terms which it subsumes.
The experimental validation of hypothesizing such higher hypotheses, defines, implicitly, a generalized notion of the relationship between man and the universe. The positive correlation of increase of mankind's potential relative population-density, with improvement of the demographic characteristics of all of the society's households, defines the relevant experimental relationship between mankind and the universe, and, thus, between the cognitive processes of the individual person in the society and that same universe.
Essentially, the experimental validation of the internal hierarchy of higher hypothesis, in this way, implicitly defines the universe as a self-bounded domain, pre-designed to bend to mankind's will when man's demands conform to valid higher hypothesizing. This is man's only possible access to knowledge of the lawful ordering of our universe. This is the sole basis for what is termed “natural law.” This is science.
'Time-Reversal':
What is Reason?
There are two distinctions in behavior which separate the human species from all animal species. One of these, which we have just addressed, is the creative power of the adequately developed, sovereign cognitive processes of the individual: the process, by means of which, validated discoveries of new physical principles are generated by original discoverers, and that generation replicated by students. The second is the Prometheus-principle, the capacity to use foreknowledge of the future consequences of changes in behavioral hypothesis, as a guide to selecting the changes in hypothesis to be adopted presently.
Since any orderable series of hypotheses is subject to an higher hypothesis, and since that higher hypothesis is relatively timeless, in respect to the hypotheses it subsumes (bounds), it is the principle of higher hypothesis which enables man to effect a “reversal of time,” such that the future efficiently determines the present.
This combination of the creative, sovereign power of the individual cognitive processes, and the efficient role of “time-reversal” within cognition, constitutes Reason.
The connection between the principle of hypothesis and the principle of time-reversal, is adequately represented in the recent paper of mine which I have already noted for reference here.20 Therefore, I limit exposition here to two illustrations. First, a summary illustration of the role of “time-reversal” in the management of a well-run modern industrial firm. Second, a comment upon de Paoli's contrast of the roles of special relativity and general relativity in the work of Albert Einstein.
First, a few relevant, prefatory remarks, situating my selection of the case of a capital-intensive industrial enterprise.
As a result of a process of willful deconstruction of the U.S. economy (among others), which has been ongoing since approximately 1966, the percentile of the U.S. labor-force employed as operatives in production of goods, has collapsed catastrophically. Whereas, at the close of World War II, over sixty percent of the labor-force was so engaged, today, it has fallen to about one-fifth. Worse, even among those surviving operatives, the levels of skill and cognitive development are vastly inferior to the qualities prevalent during the 1946-1966 interval. This is aggravated by an imminently catastrophic spiral of collapse in quality of education and cultural development of the personality, at all educational levels, throughout almost the entirety of post-war generations.21
Still worse. Thirty years ago, the overwhelming majority of U.S. adults, whether associated with industry as administration, engineers, or operatives, took pride in the contributions of production to our standard of living and national economic security. The frontiers of technological progress, in the domains of tool-making, and research-and-development, were the popularly sought, elite qualities of employment, and employee satisfaction, in our productive sectors. Today, under the ideological deconstruction brought about through the influence of such “post-industrial” utopianisms as “consumerism,” perhaps a majority of our population views the producers as “greedy, irresponsible” adversaries of the consumer. Under such conditions, even mere sanity in popular thinking about our economy, let alone what has become the relatively alpine quality of actual competence, is not to be taken for granted.
In these times, that endangered species, the technologically advancing, capital-intensive, power-intensive mode of industrial production, is almost the last bastion of sanity in the U.S. economy's daily life. The relevant, persisting, distinguishing feature of such a firm, now, as in lost, happier economic times, is that such a firm is the best choice of microcosmic reflection of the processes at work in the national and world economies as entireties. Here, the combined forces of capital-intensity and matching pressures of technological attrition, find their relatively most concentrated expression.(machine tool box)
In sum, each present moment of life of such an industrial firm, is, in itself, a microcosm of its situation in the vast economic process in development in the world at large. Immediately, that moment assumes the form of the expression of the past in the present moment's production, but, also the expression of the future development which the gains from present production must be directed to fostering. The productive process is using up physical capital invested years earlier, consuming materials and components which went into supplier firms' production months, even years earlier. At the same moment of today's produced output, there is ongoing work in preparing those capital purchases, those product designs, and so on, which will not be seen in production for months, years, or even longer, yet to come.
The most characteristic feature of that ongoing process, is change. Technological change, and also other kinds of change. Many of these changes involve modifications of the hypothesis governing production, product-design, and marketing. Forecasting—foreknowledge—is the essence of effective management: a veritably Promethean quality of foreknowledge, is the aura surrounding the great industrial managers of the modern economic history of the pre-1966 United States, and of Germany's industrial development since 1876.22
The illustration from science as such, is provided in the form of a comment on a paragraph from de Paoli's manuscript:
Einstein once wrote that his first major discovery (Special Relativity), was stimulated by the need to solve a given anomaly present in Newtonian physics. But, he added, there was no visible anomaly which pushed him to his second major discovery (General Relativity). He arrived at it after he had decided to see where the limit of the first discovery lay: where the first theory, as any theory, would break down. A society, in a sense, has the same moral imperative to search for truth. To be able not simply to react to, but to anticipate catastrophes one must know in advance. [emphasis added —LHL]De Paoli's argument here, should be restated for emphasis. He argues, that whereas Einstein's work on Special Relativity was provoked by an existing experimental paradox, the work on General Relativity was provoked by foreknowledge of a future paradox which would challenge the validity of Special Relativity.
Focus upon the antepenultimate sentence in that quoted paragraph. How should we read “limit” in that sentence? Let us substitute the term “boundary,” as we have developed it here. Restate the sentence, to reflect that substitution: “... to discover where the boundary of the first discovery lay.” That substitution implicitly removes any reader's defensible attribution of mystification to that paragraph.
The “boundary,” of course, lies within that which bounds an hypothesis, the relevant higher hypothesis, the latter relatively timeless with respect to the series of hypotheses which it bounds. To restate the point accordingly: Once we have been guided to a validated hypothesis under the guidance of an higher hypothesis, the principle of change embedded within the latter suggests the successor term of the series. The relative timelessness of higher hypothesis is thus, once again, seen at its work.
Thus, when Einstein, like his relevant contemporary, Hermann Minkowski, was impelled this way, by considerations of non-Euclidean geometry, Einstein's mind was directed toward reflection upon the precedents supplied by Kepler, Leibniz, and Riemann. In other words, toward adoption of a new higher hypothesis, the higher hypothesis of relativistic physical geometry. This, even in that form, already reflects the general nature of true foreknowledge within the setting of individual human cognition.
Recall the elegant excerpt from Minkowski's famous lecture on the subject of Einstein's formulation of so-called “Special Relativity”: that, henceforth, time, by itself, and space, by itself, must vanish, to be superseded by physical space-time. Minkowski did not fully grasp the implications of what he himself had uttered in that lecture. He had not fully escaped from the grip of the “politically correct” classroom ideology of those times, “linearization in the extremely small.”23 Nor, did Einstein's commentator Hermann Weyl escape the “politically correct” grip of this same fallacy.24 Einstein's movement away from the positivism of Ernst Mach, to which he had been conditioned, toward Riemann's, Leibniz's, and Kepler's standpoint in method, constituted at least a fair approximation of a new choice of higher hypothesis. In this way, Einstein confronted himself with the issues of whether the universe within which Special Relativity might lie, were bounded, or not.
In short, in his approach toward General Relativity, Einstein acted out of foreknowledge of a future devastating paradox, which would confront Special Relativity in the same manner Special Relativity itself had been generated as a solution for a devastating ontological paradox incurred by the then “politically correct” Newton-Cauchy-Clausius-Maxwell ideological mind-set.
The universe which de Paoli identified by Leibniz's term Immensum, is bounded, but not quite in the sense Einstein argued the point. Nonetheless, the issue of bounding was sufficient to prompt Einstein to think of the requirements this issue itself required be addressed.
Here, respecting the illustrative point at hand, relativity, the issue is not that Einstein's approach contained some error. The point here, is, that every good scientific discoverer is guided to a validatable new hypothesis—e.g., new physical principle—under the influence of a set of assumptions corresponding to what we have identified as an higher hypothesis. An higher hypothesis in any expressed approximation, such as the Einstein case indicates, implicitly begets one or more successor hypotheses to any initial hypothesis so generated.
As modern, capital-intensive industrial production provides us one illustration, the case of a science-driver “crash program” of task-oriented research and development, provides the second illustration.
Return to that classroom where bright students Johnny and Jimmy were sharing reflections on the feasibility of insight into the sovereign domain of one another's, creative, cognitive processes. Let time pass, such that all of the members of that illustrative classroom-case, are now participating in a great “crash program” science-driver teamwork, such as the U.S. Manhattan Project, or the German-American space program under the (relevant) brilliant logistics veteran of Lt.-General George S. Patton's U.S. Third Army, General (J. Bruce) Medaris, and, later, the John F. Kennedy Manned Moon-landing imperative. The first thing which Johnny and Jimmy ought to have known, by no later than the time they entered this crash program, is a few historical facts about modern “crash” varieties of science-driver programs; this knowledge would help them keep their intellectual moorings amid the sometimes storm-tossed internal life of the kind of program they are entering.
The first approximation of “crash” science-driver programs, was the Fifteenth-century Golden Renaissance, inclusive of the work of Filippo Brunelleschi and of Nicolas of Cusa's followers through Leonado da Vinci. The next notable example, is the late-Seventeenth-century science-economy mobilization, under France's Minister Jean-Baptiste Colbert. The third outstanding example, was launched in France, beginning 1792-1794, under the direction of Lazare Carnot and, his collaborator, and former teacher, Gaspard Monge. The next science-driver program was that directed by Prussia's Alexander von Humboldt, who, in collaboration with Carl Gauss, established Germany's Nineteenth-century world supremacy in physical science. The next, world-shaking “crash science-driver” leap in economy, was unleashed under the U.S. Presidency of Abraham Lincoln, which established the U.S. economy as the world's most powerful nation-state economy, and the most technologically advanced, during a period of approximately two decades.25 The sixth “crash program,” modelled directly on the U.S. precedent, was the late Nineteenth-century hitching of Germany's world leadership in science, to the development of a united Germany's economy-driver, the expansion of its machine-tool design sector.26
The U.S. Manhattan Project and the Germany-U.S.A. aerospace “crash programs,” can not be competently understood, in any economic-functional sense, until we view them as outgrowths of a modern tradition which features prominently the earlier case-histories to which I just referred. So, situate our Johnny and Jimmy, in the anteroom awaiting induction into a new “crash program.”
Nothing stimulates the creative scientific capabilities of the unblocked professional as much as a social environment in which he, or she, is prodded to replicate virtually daily, floods of original discoveries, both old ones he, or she, had not worked through earlier, but also a constant outpouring of new proposed solutions to both well-known and previously unsuspected ontological paradoxes. This is the environment for which the suitable, earlier classroom experience of our Johnny and Jimmy prepared their minds. From that classroom, Johnny and Jimmy learned many particular things; but, as we stressed here earlier, the important thing, above all else, which they came to know, was the principle of a Classical-humanist form of educational process. It is their youthful attunement to that process, which will make them valuable recruits to the program they are now entering.
Thus, when we pack together, so to speak, a large number of gifted and highly motivated professionals, together with the technicians who assist them, we have created a forcing-chamber for the relatively highest rates of scientific progress. This, on the condition that some unifying sense of purpose supplies a red thread of coherence to a complex array of diverse, relatively more short-term, often ad hoc objectives.
The connection of such science-drivers to the economy, is essentially the following.
There is an essential, underlying equivalence between the perfection of the design of a proof-of-principle laboratory experiment, and the principle underlying a corresponding, entirely new family of machine-tool designs. It is the perfected design of a proven, proof-of-principle laboratory experiment, which supplies the model of reference from which a corresponding, new set of machine-tool designs is derived. Such a machine-tool-design principle, then assumes the role of an hypothesis in generating a fertile theorem-lattice of beneficial applications.
Perhaps the most dramatic demonstration of this connection, is the unpleasant fact, that, during the present century, no leading nation of modern European civilization has generated an actual, net physical-economic profit, except under the impact of large-scale military mobilizations, either in preparation for, or conduct of what is termed modern “annihilation warfare.”27 The vast economic waste, which military expenditure represents, is certainly not the source of this net physical-economic profitability. It is, rather, the spill-over of frontier technologies, from science, into the machine-tool-design sector, under conditions of forced-draft economic growth for national security, which is the source of profitability. In these cases, the spill-over from the military into the civilian economy, results in an exceptionally high rate of improvements in design of products and of productive processes. The Germany-U.S. “crash” space-program, had a famously similar benefit for the U.S. economy as a whole.
This in no way is an argument for war. Rather, it is a demonstration of the fact, that, since the assassination of U.S. President William McKinley, only under war-time or related conditions of national urgency, are the economically depressive, parasitical habits of Wall Street and similar carpet-baggers, held in check. If we could rid ourselves of the tyranny of those monetarist and kindred parasites (and their Federal Reserve System), who were the constituency for Presidents such as Teddy Roosevelt and Calvin Coolidge, the people of the U.S. would never have experienced anything inconsistent with general and soaring economic prosperity, throughout the past century as a whole.
The points to be listed here, in summation of these illustrations, are these. First, the source of progress in both the potential relative population-density and demographic characteristics of family life, is that which Christianity identifies as the nature of each individual person, as made in the image of God. That nature is expressed by that facet of cognition, which efficiently links the individual personality to the “simultaneity of eternity,” those cognitive processes by means of which mankind hypothesizes the higher hypothesis. Second, establishing forms of social relations which are appropriate to forcing the relatively highest rates of generation, and replication, of discoveries of both physical and Classical-artistic principles, produces an individual type which represents the relatively highest degree of development of the moral character of the individual person, while it also ensures the relatively highest rates of generation and efficient assimilation of scientific, technological, and artistic-cultural progress.
Whether Einstein's General Relativity survives, or not, the nature of Einstein's motivation in that matter, as de Paoli represents this, is the key which unlocks the treasure of cognition, and presents the greatest ration of its benefits to mankind generally. Rather than responding only to the goads of present failure, as which a devastating ontological paradox forces itself upon us, it were better to act out of a conscience governed by foreknowledge, including foreknowledge of those issues of principle which will forseeably oblige us to abandon what we often cuddle as “our traditional culture.” Prevent the disastrous consequences of sins of omission now, before they become the ruinous sins of commission which bring our civilization down.
Generalized Analysis Situs:
Simultaneity of Eternity
The standpoint of Leibniz's Analysis Situs obliges us to reorganize the presently popular notion of science according to the implications of a nine-cell matrix. We must divide the empirical evidence of science among three types of processes, and the evidence bearing on all processes among three well-defined categories. The notions of the three types, we derive from a careful scrutiny of the traditional distinctions among non- living, living, and cognitive processes. The three categories of evidence, are astrophysical, microphysical, and macrophysical.
The relations among the nine cells so established, are ordered as follows.
The three types are distinguished by their respective differences in internal ordering. The division between living and non-living processes, for example, is implicit in the moment of transition from a living (anti-entropic) to a dead (entropic) ordering of biological organization. The difference among living processes, is between cognitive and non-cognitive processes (as the anti-entropic ordering of cognitive processes has been distinguished so here).
The distinction among types of evidence, pertains to the effect of the inhering limitations of the human sense-apparatus, respecting the observation of ordering-relations among phenomena. For example: How did a culture, living, for several thousand years in Central Asia, during a time the Vernal Equinox was in the constellation of Orion, construct an approximately 26,000-year equinoctial cycle? It was through the astrophysical methods of constructing solar-sidereal calendars, that man developed those methods of astrophysical investigation, the which were then applied to develop, first, macrophysical science, and, next, supply, from astrophysics, the methods of necessary and sufficient inference upon which a competent microphysics relies.28
Once the requirement for a generalized Analysis Situs is recognized, the currently popularized views on scientific specializations must be subordinated, by placing the primary emphasis upon efforts to master the nature of the combined interrelations among the nine cells defined by the just-described types and categories of evidence. Each of all possible permutations of the nine cells, corresponds to an actually existing experimental subject-area of generalized Analysis Situs. Science is then primarily located in that hypothesizing of the higher hypothesis which subsumes each and all of these permutations under a commitment to satisfy the requirements (sooner or later) of a single conception of universal ordering-principle.
The experimental basis for such a generalized Analysis Situs, is located within the domain of the science of physical economy: mankind's essential existential interrelationship within the universe as, in every possible sense, an entirety. That is to say, the experimental basis for a competent general notion, which distinguishes between what is, and what is not to be considered “science,” lies in the evidence of that “Great Experiment,” the which is mankind's total relationship to the universe as a whole. The subject of science is mankind's willful relationship between the ordering of transformations within the universe, as correlated with both the increase of human potential relative population-density in the universe (relative to the Earth's surface), and the improvement of the demographic characteristics of households in the human population taken in its entirety.
These scientific ideas must incorporate the efficient role of “time reversal.” “Time reversal” is to be understood, not merely as foreknowledge in its simplest expression; the possibility of the efficiency of such foreknowledge within this universe, must be taken into account as showing us the necessary functional character of the lawful ordering of the physical universe. That man could exist, to command the universe to increase our species' potential relative population-density, with accompanying improvement of the demographic characteristics of households, signifies that the willful aspect of man's efficient relationship to the universe, is an integral potential embedded in the adducible design of the laws of the universe.
Once we situate science thus, there is no law of universal entropy in this universe. The universe submits to mankind, only when man's command is intrinsically anti-entropic. The law of the universe, in the only way we could know its law, is the law of universal anti-entropy. The principle of anti-entropy, so situated, is the fundamental principle of science.
To grasp the more deeply underlying implications of this, extend the successful self-development of this “Great Experiment” forward and backward in time, without straining toward the non-existent “infinity” which hesychastic fools seek to touch. The boundaries of existence the universe, are not to be found in some distant past, some distant future, or, far, far away. Man's mind locates the actual boundary, as Nicolaus of Cusa did, in that which bounds hypothesizing the higher hypothesis, which is Plato's notion of the Good, Plato's notion of an efficient agency located within no lesser domain than the simultaneity of eternity.
If we but extend the process of hypothesizing the higher hypothesis respecting the relations internally characteristic of this universe, that hypothesizing represents a series of higher hypotheses. That sequence is time. If we treat this “time” as any other dimensionality of a Riemannian universe, as Riemann's discovery demands that we treat time so, then the ontological unity of time defines the series representing the Manyness of the universe as a whole as a One, which Plato named the Good, and defines that One as the relatively timeless, efficient existence, inhabiting and ruling the simultaneity of eternity. The necessary existence, within the domain, of the Good, as that existence shown by the characteristics of the domain itself, is that which bounds the domain, and defines it as a self-bounded domain. God created this universe, and bounds it, but, always and forever, from the inside. This, as Leibniz rightly insisted, is the best of all possible worlds.
There are no “yardsticks,” of any kind, existing outside this universe, this self-bounded domain whose limits are the simultaneity of eternity. There exists no external place, from which an observer might contemplate the universe; there is no deus ex machina. The universe can be known only from the inside. The test of such latter knowledge, is securing the proof of the existence of the would-be observer as an efficient actor occupying a necessary place within the universe which is to be observed. That is to emphasize, that the first question the would-be observer must address, is the question whether the observer himself exists, the question which Rene Descartes so flagrantly flunked.
We know we exist within the universe, when we begin to change that universe for the better, when we begin to realize the inborn, special potential of the human individual, the cognition whose power to make miracles fascinated our Johnny and Jimmy. Somewhere, in the higher reaches of hypothesizing the higher hypotheses, mankind is known to exist as the kind of special creature whose innermost nature, whose outermost efficiency, Johnny and Jimmy were exploring in the classroom. Man exists because man is needed. The nature of this need is obvious; man is deployed, as the agency assigned to change this universe, from within: to improve it, and, in the process, to improve the moral character of the individual person, as Johnny's and Jimmy's moral character was being improved by the characteristics of the kind of good, Classical-humanist education they were enjoying in that classroom.
Appended Remark:
Eratosthenes' Estimate for the Spheroid
In my description of Eratosthenes' measurement of the curvature of the astrophysically-determined south-north distance from Syene (Aswan) to Alexandria, I chose to omit from that discussion of the matter, a collateral fact, which Eratosthenes must, necessarily, have taken into account, but which was not explicitly addressed in the putatively original accounts of that experiment available to me [see Figure 1]
It is a point whose crucial implications are made clear, more than 1800 years after Eratosthenes, by the revolutionary achievements of Johannes Kepler and Carl Gauss in astrophysics. This bears upon a point which I did address, later, in reference to this point as it arose to be a central feature of Bernhard Riemann's habilitation dissertation.
Factually, the omitted point is deceptively simple. In this case, as is not uncommon in the history of science, once we challenge ourselves to determine whether a simple fact is also a mathematically-physically elementary one, as in the case of the development of what I referenced, on page 28, as the Ampere-Weber proof of the existence of an “angular force” in electrodynamics, we find ourselves confronted by proof that the relevant, elementary principle of science, is usually expressed in deceptively simple, often overlooked appearances.
In the text of the manuscript, I recounted the placement of sundials along a measured (walked), south-north distance, in Egypt, from Syene (the ancient site of Aswan), to Alexandria. I pointed to the difference in angles of the noonday shadows of the gnomons, at the extremities of that measured distance. I pointed to the arc defined by the difference between those two angles, as corresponding to the distance from Syene to Alexandria. In my paper, I skipped an intermediate step: did Eratosthenes merely assume that that arc was a spherical one, or had he taken some precaution which gave him persuasive evidence that the arc was situated in a spherical geometry, or nearly so?
I assumed that he had; thus, with good conscience, I was able to keep my account of the experiment limited to the barest principles underlying the proof of curvature itself. In this present location, I do a bit more, than merely supply the defense of my editorial assumption on this simple point. To aid the reader in discovering my deeper purpose here, I provide the design of an illustrative figure. [see: Figure 3] In this figure, I close in upon a finer detail of the actual Eratosthenes experiment. Having placed that figure on the implied blackboard, I describe what I have drawn, as follows.
Let the curved line S → A represent the measured south-north line from ancient Syene to Alexandria. We have Eratosthenes' hemipherical sundials placed at point S, and point A. We also have similar sundials placed at measured (walked) intervals, p1, p2, p3, ... , between S and A, along line S → A. Now, by construction, we may compare the angles, qs, q1, q2, ...,qA, corresponding to the pre-measured arcs of the series S-p1 , p1-p2 , p2-p3 , ....|....|
Also, by construction, we may compare the measured lengths of those arcs. We may, similarly, compare the ratios among those measured arc-intervals (into which arc S → A is divided by the placing of these sundials), to the ratios of the differences in the angles subtending those arc-intervals. In short, the construction of the experiment, shows that Eratosthenes designed the experiment in such an axiomatic way, as to provide for a simply geometrical determination of the relative degree of self-similar constancy of the rate of curvature along line S → A.
In my experience of the manifest behavior of the human mind, design of experiment expresses intent, whether that intent is witting, or not. Thus, we know, by study of the structure (design) of Leonhard Euler's argument, that in his defense of what was expressed later, as Augustin Cauchy's castration of the calculus, by a “limit theorem,” that Euler was not merely mistaken, but intentionally so. The fact, that a mind as sophisticated in formal mathematics as he was, could present as proof, a theorem axiomatically pre-embedded in his design of the supposed proof, is clear showing of his intent to commit a fraud. Thus, the internal evidence of his own argument, shows that he perpetrated a fraud. This is the fraud, which, notably, was continued after him, as in the tradition subsuming Lagrange, Laplace, Cauchy, Grassmann, Clausius, Lord Kelvin, Maxwell, Hermite, Lindemann, Felix Klein, Bertrand Russell, Norbert Wiener, and John Von Neumann, as also Theodor von Karman's Anglolphiliac revision of the work of Bernhard Riemann and Ludwig Prandtl in hydrodynamics.
On the basis of that evidence internal to that micro-design of Euler's hoax, we are, thereafter, not merely justified, but obliged, to take into account Euler's political situation, as a devotee of Frederick II's Berlin chapter of a rabidly gnostic, Newton cult, which had been created by Venice's Paris-based spy-master, Abbé Antonio Conti (1677-1749). After Conti's death, the connections were maintained by Venice's notorious Italian asset, Francesco Algarotti,1 by such other sub-agents as Voltaire and Giammaria Ortes. Euler's controlling role in the Berlin cell of Conti's network of Leibniz-hater salons, locates the proximate source of Euler's motive in perpetrating the hoaxes later associated with doctrines of “linearization of space-time in the infinitely small,” and with the ensuing, purely mythical assertion, by empiricists and positivists, that the discovery of the transcendental quality of pi (&Mac185;), is to be credited to the politically motivated, algebraic hoaxes perpetrated by Euler, Lambert, Hermite, Lindemann, et al.
The crux of the issue implicit in this issue of constant curvature in the small, is pinpointed by my reference to the concluding line of summation in Bernhard Riemann's 1854 habilitation, as referenced in footnote 14.I freely translate the two most relevant excerpts from within the second paragraph of the dissertation's concluding section 3.
Riemann begins that paragraph, by qualifying his ongoing argument there, that: “If one presumes, that a body exists independently of its position, then the measure of curvature is constant throughout, and, it then follows, from astronomical measurements, that that curvature can not deviate from zero. ... However, when such independence of position does not occur, one can not accept the [presumption] that relations of measure (Massverhältnissen) in the macroscopic domain [apply] to the infinitesimal [domain]. ... It is, therefore, plausible, that the relations of measure of spatial relations in the infinitesimal, do not conform to the presuppositions [e.g., definitions, axioms, and postulates] of geometry. In fact, one would be reasonably compelled to that [view], as soon as this would permit the phenomena to be clarified in a simpler way.”
Then, the concluding sentence of his dissertation wraps up the line of argument just referenced: “This leads us into the domain of another science, into the domain of physics, which the nature of today's occasion [on mathematics as such] does not permit us to enter.”
The same point was repeatedly addressed by the same Gottfried Leibniz, whose contributions the political circumstances of 1854 Göttingen university did not permit professorial candidate Riemann to mention in safety. Notably, the entirety of Riemann's leading discoveries, including the habilitation dissertation and his later work on Analysis Situs and hypergeometry, are the product of Riemann's rich study of Leibniz's work,2 a study whose fruit was powerfully enriched by the relevant additions by Carl Gauss, as, also, by Johannes Kepler. See Gauss, on such related topics as bidquadratic residues, curvature, and hypergeometry; Leibniz's references to Analysis Situs are central features of this influence, as expressed, with great emphasis, in Riemann's habilitation dissertation, as, also in his leading later discoveries.
Leibniz's calculus, as presented to a Paris publisher in 1676, was developed in response to specifications supplied by, chiefly, Johannes Kepler, but also Blaise Pascal, before him. This arose, in Kepler's work, around the practical matter of determining the curvature of a non-circular (e.g., elliptical) planetary orbit. Thus, for Leibniz, the essence of the calculus, is the issue of the determination of a non-constant curvature occurring within infinitestimal intervals, just as this is the central practical mathematical feature of Riemann's habilitation dissertation. This is the central feature of young Carl Gauss' celebrated stroke of genius as a physicist, in determining the orbit of the asteroid Pallas; it is the basis for Gauss' subsequent, richer development of the science and practice of both geodesy and geomagnetism. This is the same issue which I am addressing here, respecting the implications of Eratosthenes' placing a series of sundials, at measured intervals, along an astrophysically determined, south-north line.
Leibniz's argument may be summed up: Given, a tangent to a line, located within the distance of some infinitesimal point of the process which that line is constructed to represent; how do we measure the non-constant curvature of that entire line, by means of local non-constant curvature within the infinitesimal region associated with that tangency? Thus, the devastatingly destructive implications for science of the fraud of “linearity in the small,” as assumed by Abbé Antonio Conti's English agent, Dr. Samuel Clarke, as developed by Leibniz-hater Leonard Euler, and, as passed from Euler, through Lambert and Lagrange, along the Laplace-Cauchy-Clausius-Hemholtz sewer-pipe of reductionism, into the intellectual cesspool of contemporary radical empiricism.
This idea was not original to Leibniz, nor to the Kepler who inspired the calculus as an intended access to solutions for precisely this mathematical problem. Its origins in modern science are found in the work which founded modern European experimental physics, Cardinal Nicolaus of Cusa's De docta ignorantia. This is a matter addressed, once more, in the paper referenced by this commentary on Eratosthenes' principal contribution to the roots of modern geodesy. The modern history of treatment of this problem of non-constant curvature, began with Cusa's original discovery of a crucial sub-class of incommensurables, later termed, by Gottfried Leibniz and his associates, as “non-algebraic” magnitudes, or “transcendentals.” Cusa proved the existence of such magnitudes for the case of the circle and sphere, by showing the relevant elementary error included in Archimedes' treatment of the subject of quadrature, as I recapitulated Cusa's argument, and its leading implications, in my 1992 “On The Subject of Metaphor.”3
The solution to the problem posed by the problem of non-constant curvature posed by experimental physics, appeared on the horizon with Gauss' development of the principles and uses of bi-quadratic residues into a general theory of curved surfaces. Gauss' work gave a new, sane, experimental meaning to what had been the grotesquely mislabelled category of “imaginary numbers,” and laid the basis for future advances into still higher orders of cardinalities.
Sometimes, what appears simple, is actually elementary; in that case, the issues involved are never simple.
1. The author of Il Newtonismo per le dame (Newtonism for ladies), and artistic advisor for the design and decoration of Frederick II's Sans Souci palace.
2. E.g., on Analysis Situs: Loemker, pp. 248-258. See also, in the same volume, Monadology, pp. 643-53.
3. Op. cit.
|
Footnotes |
||
1. Dino de Paoli, “Was Darwin an Evolutionist, Or Just a Social Reformer?,” 21st Century Science & Technology, Fall 1997 (Vol. 10, No. 3) (to be published).
2. Most notably, in his Timaeus.
3. As de Paoli references this: Gottfried Leibniz, “Correspondence with Arnauld,” in Gottfried Wilhelm Leibniz: Philosophical Papers and Letters ed. by Leroy E. Loemker (Dordrecht: Kluwer Academic Publishers, 1989) [hereinafter referenced as “Loemker”], pp. 331-350.
4. Between the ages of twelve and eighteen years, I engaged in an intensive course of study, in chronological order, of the most celebrated Seventeenth and Eighteenth centuries' philosophers of England, France, and Germany, from Francis Bacon through Immanuel Kant. By mid-course, I had become a follower of Leibniz; I occupied the last two of those years both studying Immanuel Kant's Critique of Pure Reason (in English translation), and refuting its implicit attacks upon the standpoint of Leibniz. It was from study of Leibniz that I learned the method of Plato; moreover, everything subsequently learned in this matter, assures me that Leibniz's view of Plato is the correct one, and contrary readings in error. From that standpoint, the Republic is indispensable for grounding one's approach to the later works. On the authority of principles of certainty which I define in these pages, these later works of Plato, I know, with certainty, address the implications of the ontological paradox posed in the Parmenides.
5. Bernhard Riemann, Über die Hypothesen, welche der Geometrie zu Grunde liegen (“On the Hypotheses Which Underlie Geometry”), in Bernhard Riemanns Gesammalte Mathematische Werke, ed. by H. Weber (New York: Dover Publications reprint, 1953), pp. 272-287.
6. Executive Intelligence Review, Oct. 11, 1996 9Vol. 23, No. 41). [Also, in Fidelio, Winter 1996 (Vol. V, No. 4)].
7. I knew Leibniz's notion (and, therefore, Plato's) of “simultaneity of eternity” as a self-bounded domain, from my adolescent studies. A new line of approach, the one represented here, was opened up for me by an early 1952 review of my then ongoing discoveries in physical economy from the standpoint of first, Georg Cantor's notion of the transfinite, and, then, later that same year, a rereading of Riemann's habilitation dissertation from the vantage-point in physical economy which Cantor had assisted me in achieving.
8. Cf. de Paoli, “Was Darwin an Evolutionist?,” Part 2, passim.
9. “XVIII. Eratosthenes,” in Greek Mathematics, trans. by Ivor Thomas, “Loeb Classical Library” (London: William Heinemann Ltd., 1980), pp. 260-273.
10. Ricardo Olvera, “Columbus and Toscanelli,” Fidelio, Spring 1992 (Vol. 1, No. 2).
11. Thomas, op. cit. Readers should attempt to replicate this simple experiment with means corresponding to those available in Third-century b.c.: Egypt; thus, they would learn respect for the degree of precision achieved by Eratosthenes, and in Columbus' map of the world, the one drawn by the Paolo Toscanelli who also instructed Columbus on some relevant points, in their correspondence.
12. B. Riemann, on his specific debts to Carl Gauss for the sources of his own revolutionary discovery, op. cit., pages 273 (biquadratic residues) and 276 (curved surfaces). The prime Gauss references are (originally): On biquadratic residues, the famous, variously translated Theoria residuorum biquadraticorum [first treatise, 1-23, 1828; second treatise, 24-76, 1831-32]; on curved surfaces, the “Copenhagen prize essay” of 1822, and the variously translated Disquisitiones generales circa superficies curvas of 1828: Carl Friedrich Gauss Werke (Hildesheim-New York: Georg Olms Verlag, 1981), Vols. I, II, IV. German translations of the two parts of the paper on biquadratic residues are found, in Untersuchung über Höhere Arithmetik von Carl Friedrich Gauss, ed. by H. Maser (New York: Chelsea Publishing Company, 1981), pp. 511-586.
13. De docta ignorantia (1441). See, Lyndon H. LaRouche, Jr., “On The Subject of Metaphor,” Fidelio, Fall 1992 (Vol. 1, No. 3).
14. Naturally, we are referencing the types of series in which the differences are not of a simply mathematical form, in which the essential feature of the ordering of the difference includes a qualitative feature, as Riemann echoes Leibniz in his crucial observation (op. cit., p. 285-286): Wenn aber eine solche Unabhängigkeit der Körper vom Ort nicht stattfindet, so kann man aus den Massverhältnissen im Grossen nicht auf die im Unendlichkleinen schliessen; .... Es führt dies hinüber in das Gebiet einer andern Wissenschaft, in das Gebiet der Physik, welches wohl die Natur der heutigen Veranlassung—LHL] nicht zu betreten erlaubt. This was already Leibniz's argument, a century and a half earlier, as de Paoli stresses the relevant issue in Part 2 of his paper, under “The Continuity of Forms: Similarity.” The fact, that we must depart mathematics for physics, as Riemann demands, does not mean we are helpless to discover efficient notions of functional ordering which are different from customary mathematical ones, but no less rigorous, and, indeed, far more powerful. We turn to a crucial aspect of that in the two concluding sections of this epilogue.
15. “Function,” in this instance, is subsumed by the notion of Analysis Situs, rather than “algebraic function.”
16. Of course, Gottfried Leibniz had made that specific argument, repeatedly, more than a century before Riemann. However, it was politically unsafe for any candidate for habilitation to present openly any explicit or implied praise for the reputation of Leibniz, or to omit ritual praise for Isaac Newton, in the Hannover still ruled by the British royal family, where Göttingen university was located. The published output of Carl Gauss, as that of his protégé Bernhard Riemann, is the product of faithful students of Leibniz, who held Newton's work in that contempt which certain of Riemann's posthumously published writings state most cogently. However, for the same British political reasons which impelled Gauss to refuse to publicize his own discovery of non-Euclidean geometry, Riemann, in his habilitation dissertation, not only suppressed acknowledgement of Leibniz's work, but supplied ritual passing praise for the Newton whose scientific claims Riemann held in contempt.
17. “The Essential Role of 'Time-Reversal' in Mathematical Economics,” op. cit.
18. Riemanns Werke, op. cit., pp. 509-538
19. E.g., LaRouche, op. cit., passim.
20. Op. cit.
21. If present trend-rates continue, we are not far distant from the state of affairs, in which the following hypothetical incident might become commonplace. A pollster, employed in going from door-to-door, reports that when he asked the respondents whether or not they were in favor of democracy, the overwhelming majority replied, “Yes.” However, when he asked those same persons, if they have voted in the preceding general, more than fifty percent replied with the question, “What is voting?”
22. See Anton Chaitkin, “Leibniz, Gauss Shaped America's Success,” Executive Intelligence Review, Feb. 9, 1996 (Vol. 23, No. 7), pp. 22-57. See also “How Henry Carey and the American Nationalists Built the Modern World,” The New Federalist, June 2, 1997 (Vol. XI, No. 21), an edited transcription of Chaitkin's May 10, 1997 presentation to an FDR-PAC Policy Forum. The complete FDR-PAC Policy Forum, which also includes Lyndon H. LaRouche, Jr.'s “The Significance of FDR for Today,” is available on videotape from FDR Political Action Committee, P.O. Box 6157, Leesburg, VA 20178 (No. FDP 97-011, 180 minutes).
23. E.g., Raum und Zeit (1907). There are usefully provocative implications in Russian mathematician Minkowski's scientifically flawed adherence to the cause of a compatriot, Nicolai Ivanovich Lobachevski. The mathematical formalist's shortfall in Minkowski's argument, was the subject of a paper by Dr. Johnathan Tennenbaum, “A Topological Shock-Wave Model of the Generation of Elementary Particles,” Executive Intelligence Review, Feb. 1, 1983 (Vol. 10, No. 4). On Gauss' view of Lobachevski's Geometrische Untersuchungen zur Theorie der Parallellinien [“Geometrical Investigations on the Theory of Parallels”] (Berlin: 1840), see a relevant remark by Carl Gauss to H.C. Schuhmacher, in concluding paragraph of a letter of Nov. 28, 1846: Carl Friedrich Gauss-H.C. Schuhmacher Briefwechsel, III (Hildesheim-New York: Georg Olms Verlag, 1975), pp. 246-247. This is the location in which Gauss dated his own discovery of a non-Euclidean geometry to 1792, a relevant claim which is borne out by close examination of the plan of action subsuming Gauss' Disquisitiones arithmeticae considered in entirety. Compare with Lobachevski's last published (1855) views on this subject, Pangeometrie (1858), which had first appeared in Russia about the time of Gauss' death. Provocative, but ultimately a fatal short-fall, is Lobachevski's use of spherical action, a less general consideration than Riemann's [see footnote 12, above] “Wenn aber eine solche Unabhängigkeit der Körper vom Ort nicht stattfindet, so kann man aus den Massverhältnissen im Grossen nicht auf die unendlichkleinen schliessen..”. As Leibniz warned, any such use of simply curved metric, implies the same ontological error against which we are warning here. Lobachevski, like Minkowski after him, was unwilling to make the final, crucial break with mathematical formalism, thus to enter, wholeheartedly, the domain of experimental physics.
24. Hermann Weyl, Raum, Zeit, Materie (1918), and expanded English edition Space, Time, Matter (1922) (4th ed.) (New York: Dover Publications [reprint], 1950). See, again, footnote 12, on the issue of this fallacy.
25. Anton Chaitkin, op. cit.
26. Ibid.
27. This is a definition exemplified by the notions of Alfred Graf von Schlieffen's Cannae: The Principle of the Flank, and also his design of the so-called “Schlieffen Plan.” “Annihilation” does not signify exterminating some large number of people, military personnel and, or others, but, rather, annihilating the adversary's capacity needed to continue organized warfare, as the Confederacy was destroyed by the combination of Sherman's “hammering” right flanking attack and Grant's bloody “anvil.”
28. One of the best demonstrations of this point, is the history of the Ampere-Weber discovery of the implications of the macrophysical angular force of electrodynamics for understanding of the ordering of electrodynamic relations within microphysical relations on the scales of atomic and nuclear physics. See Laurence Hecht, “The Significance of the 1845 Gauss-Weber Correspondence,” 21st Century Science & Technology, Fall 1996 (Vol. 9, No. 3). back to addendum
by Lyndon H. LaRouche, Jr.
Dec. 7, 1996
This article was originally published in the 1996-97 EIR Special Report on the "Eurasian Landbridge: Locomotive for World Development."
Until about thirty years ago, when we went collectively mad, production used to be a pipeline, through which the benefits of technological progress flowed more or less continuously. For the production manager, who was concerned with products to be put on line as much as five to ten years hence, and with the phase-out of obsolete or worn-out plant and equipment a dozen or so years ahead, the “pipeline” was a process, filled with planning of future technological change in products and processes. The scope of any respectable firm's planning function was seldom less than a generation's span. Key to the technological change constantly in progress in any such large firm, was the role of the relatively small, high-technology firm which specialized in a range of machine-tool design and related specialties. The competitiveness of production, respecting quality of product and productivity, was derived from a relatively continuous process, generally hidden from the public—behind the scenes, so to speak, of technological improvements in product and processes.
|
Figure 3: How the “Machine-Tool Principle” is situated.
|
||||||
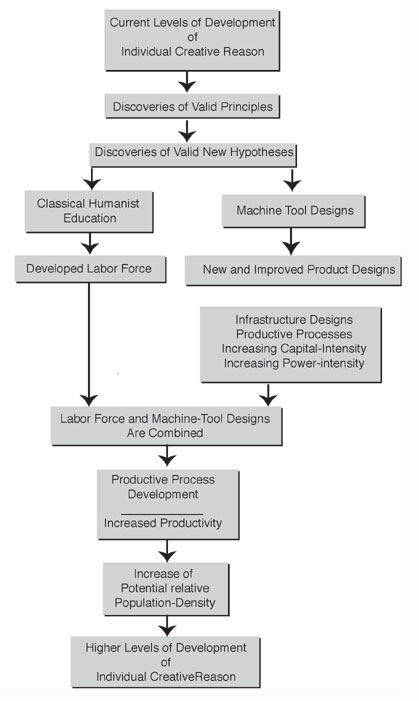 |
||||||
View that “relatively continuous process ... behind the scenes, ... of technological improvements in product and processes,” from the vantage-point of the general physical-economic function identified here at several points earlier. That the ratio of “free energy” to “energy of the system” must not decline, despite a constant, required increase in “energy of the system,” per capita of labor-force, per family household, and per unit-area. It is the constant increase of productivity and product quality supplied to the productive process, chiefly through the machine-tool-design factor, which meets that requirement. The requirement is not satisfied by “getting cheaper parts from elsewhere”; it requires securing a cheapening of the effective cost by relying upon sources which have high rates of technology-driven improvements in productivity and product....
The secret of sustainable economic growth and profit, is high rates of high-density technological progress in every possible pore of the productive process. It is not how cheaply we might import from cheap-labor markets abroad; it is not simply a matter of whether we are exporting jobs our people need. It is the density of such technological progress in production, per capita, per family household, and per unit-area in one's own national economy, which determines whether one's national economy is growing, as ours used to do, until about thirty years ago, or, like our own today, collapsing into bankruptcy through the kinds of policies which have taken over the United States during the past thirty years, up through the present day...
The principle is: do not think of this as a matter of buying products; it is a matter of buying change. When you buy a product, are you also buying into the quality of change you will need for tomorrow? Are you buying into yesterday, or tomorrow? Production, and successful national economy, are both all about technological change. Therefore, the board of directors member, or operating executive, who does not understand that, should be fired with the same sense of urgency prompted by the detection of a chronic embezzler, pyromaniac, or axe-murderer in those positions.
Behind all this, is education, as Lothar Komp stresses the relevant point. The transmission of knowledge from the education and scientific-research institutions, into production, occurs chiefly in the conversion of validated experimental designs for proof of principle into the form of machine-tool designs by organizations such as the Mittelstand firms on which Komp focuses our attention. (Lothar Komp, “The Crucial Role of the ‘Mittelstand’ in the Economy of Postwar Germany,” Executive Intelligence Review, Jan. 1, 1997 (Vol. 24, No. 1).
This is the structure for technological progress: From Education, to Experimental-Scientific Discovery, to Machine-Tool Design, to Production Process and Basic Economic Infrastructure, to Product and its physical distribution. This structure is rooted in natural principles; but, the elaboration of such a structure into the realized institutional forms of modern nation-state economies, is a production of a political-economic revolution launched by the 1439-1440 sessions of the great ecumenical Council of Florence. The keynote of that effort, was the building up of France's Dauphin, preparing him to become the Louis XI who established the first known nation-state in human existence: a society in which the intelligentsia drawn from the educated portion of a general citizenry emerged to challenge the reactionary authority of both the landed and financier oligarchies of feudal Europe. The process of state-backed educational programs, to transform growing portions of the ordinary citizens into a national intelligentsia, while fostering high rates of infrastructure-building, and agricultural and industrial progress, is the germ, planted in Louis XI's France, out of which the modern European nation-state economy developed, a revolutionary change in political society and economy, which, despite all evils perpetrated in the name of European civilization during this same period, had resulted, until thirty years ago, in the highest rate of progress in the human condition, in the planet as a whole, qualitatively greater than in all human existence earlier.
Without the appropriate quality of education, the kind of education which has been systematically destroyed during the past thirty years, the entire system of modern civilization must collapse into a “new dark age,” whatever other errors of policy might affect the economic process. Without the fostering of high rates of experimental-scientific research, the economy must collapse, whatever the quality of other aspects of economic policy-shaping. Without the link between science and production provided by the sector of the economy devoted to machine-tool design, a similar catastrophe becomes inevitable.
What is the Schiller Institute?
Fidelio Table of Contents from 1992-1996
Fidelio Table of Contents from 1997-2001
Fidelio Table of Contents from 2002-present
Beautiful Front Covers of Fidelio Magazine

Join the Schiller Institute,
and help make a new, golden Renaissance!
MOST BACK ISSUES ARE STILL AVAILABLE! One hundred pages in each issue, of groundbreaking original research on philosophy, history, music, classical culture, news, translations, and reviews. Individual copies, while they last, are $5.00 each plus shipping
Subscribe to Fidelio:
Only $20 for 4 issues, $40 for 8 issues.
Overseas subscriptions: $40 for 4 issues.
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps |
Dialogue of Cultures
© Copyright Schiller Institute, Inc. 2005 All Rights Reserved.