
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps
Dialogue of Cultures
 |
||
|
Lyndon H. LaRouche, Jr.
|
||
The Classical Principle in Art and Science
by Lyndon H. LaRouche, Jr.
September 29, 1997
Part I
This article is reprinted from the Winter 1997 issue of FIDELIO Magazine.
For related articles, scroll down or click here.
For Related Articles
Go to Part I Footnotes
Go to Part II
On the surface, the pervasive degeneracy of today's popular culture, seems to have been unleashed by the rock-drug-sex counterculture introduced to the U.S.A., from Britain, as a new mass-culture, since the middle of the 1960's. In fact, today's popularized, existentialist counterculture, is merely the terminal phase of an approximately century-long, global process of degeneration of the culture of European civilization. I shall show here, that that foregoing judgment of mine is not be viewed as a mere matter of my choice of taste, but corresponds to a scientifically determined matter of truth; nor is the phenomenon an inevitable outgrowth of that mystical process which G.W.F. Hegel and his crony, Karl F. Savigny, identified, as the Weltgeist, Zeitgeist, or Volksgeist. I shall demonstrate, that the most recent three decades is distinct from preceding phases, as it represents the terminal phase of a century-long process of popular cultural decay.
The argument to be demonstrated here, is, specifically, that the present existentialist trend in current, relevant majorities' academic and other opinion, is most fairly described, as a form of mass psychosis. As a psychosis, it is, in historical perspective, as Barbara Tuchman's A Distant Mirror1 implies: an epidemic mental disorder, akin to the spread of the Flagellant and related, lunatic cults during the middle of Europe's Fourteenth-century "New Dark Age." The proliferation of wildly gnostic and even outrightly satanic charismatic cults, including the late Queen Victoria's British-Israelite cult, echoes, and typifies, the mass-insanities spread in the name of religion, during that "New Dark Age."
Like Europe's mid-Fourteenth-century proliferation of mass-psychotic cults, the collapse of European culture to today's levels of morbidity, did not occur all at once, nor has the Classical European culture of 600 B.C.E.—A.C.E. 1900 vanished entirely, even at this point. Around the world, as during Europe's middle- to late-Fourteenth century, there is still a relative, if diminishing handful of scientists, as of performing artists who can reproduce the levels of thinking represented by the greatest poets and musicians of Nineteenth-century Europe and North America.
However, those qualifying exceptions noted: In the main, in virtually all parts of the world, as typified by the spread of the satanic cult of rock into religious services, even into the churches in Rome, the recent cultural state of affairs is a disaster inflating itself into a catastrophe. As for science: typified by the influence of the celebrated "ozone hoaxster" F. Sherwood Rowland, most recent science graduates no longer know what science is.
Today's trends in popular culture parallel syphilis, tuberculosis, or AIDS. It was not spread as an epidemic of sudden death, such as bubonic plague; it has developed as a lingering, degenerative disease. It is, in fact, a mental disease, which must be considered, functionally, as either an expression of mass psychosis, or as tantamount to a mass psychosis. That is, this popular culture represents systematic damage to that specific mental function which distinguishes the human species from the beasts. It represents the degeneration of the functioning of the individual human mind, from the characteristically human reliance upon cognitive capabilities, to domination by a relative bestial, "lemming-like" emphasis upon "politically correct," emotional-associative behavior.
In U.S. history, for example, the high-water marks in North American culture are represented by the close associates of the principal architect of our freedom, Benjamin Franklin, and the rallying of this republic to become its true self, by President Abraham Lincoln. As the very language of the 1776 U.S. Declaration of Independence and of the Preamble to the U.S. 1789 Federal Constitution expresses this, the circle around Franklin adopted the leading ideas of Gottfried Leibniz, in rejection of the moral degeneracy characteristic of the British empiricism of John Locke. Boston opium-trader, Manhattan banker, and Confederate slave-owner, typify the moral degeneracy which our patriots were obliged to combat within our own borders, and from abroad. The crushing of the treasonous Confederacy, under the combined leadership of Henry Carey, Abraham Lincoln, and Generals Grant and Sherman, continued to be the high-water mark of morality in the U.S.A., into the generation which fought World War II, and slightly beyond. However, unlike Presidents Franklin Roosevelt and Jack Kennedy, Presidents Teddy Roosevelt, Woodrow Wilson, and Calvin Coolidge were in no sense patriotic, or even moral. It was the rise of the influence of the defeated Confederacy to power in Washington, once more, through such spawn of the Confederacy as Teddy Roosevelt and Ku Klux Klanner Woodrow Wilson, which marks the extended process of moral decay of U.S. culture over the course of this century to date, a moral degeneracy which accelerated under the post-Kennedy rise of the rock-drug-sex youth-counterculture, to become the hegemonic influence in academic life today.
Until now, the last gasp of mass-based, true patriotism in the United States, was the role of the Lincoln tradition's influence on President John F. Kennedy's generation, in mustering support from themselves and their children, for the great Civil Rights resurgence of the early through middle 1960's. After the events of 1968, morality, culture, and the Franklin-Lincoln tradition of patriotism, seemed to have vanished from the opinion of the majority, sunk into the quicksand of the countercultural swamp of "post-industrial" utopianism.2
Thus, over the course of the recent three-hundred-odd years, since the dictatorship of William of Orange, established in England in the events of 1688-89, the ebb and flow of culture and morality in English-speaking North America, can be traced in terms of generations. The post-World War II generations have been, overall, a cultural disaster. Only a great cultural shock, analogous to the period of Civil War under President Lincoln, could bring the members of those generations back from post-industrial fantasy-life, into the realm of reality.
The prompting of today's moral and cultural decay in the U.S.A. and Western Europe, is more quickly, and usefully recognized as the combined impact of the 1962 "missiles crisis," cover-up of the Kennedy assassination's perpetrators, and nightly TV images of the Vietnam War, into terrifying the overwhelming majority of the "Baby Boomer" generation into a mass, "lemming-like" flight from reality, into the so-called youth-counterculture of the middle to late 1960's.3 The results of that "shell-shocked" state of virtual mass cultural psychosis have been, first, the spread of an existentialist counterculture echoing the doctrine of Nazi philosopher Martin Heidegger and such Heidegger clones as France's Jean-Paul Sartre, Jacques Derrida, and Frantz Fanon. Second, over the course of the recent thirty years of erotic "Post-Modernism," the university students of the mid-1960's have come to occupy nearly all the topmost positions in government, business, education, the artistic professions, and the mass entertainment and "news" media.
Once more, what I have expressed, thus, is no mere opinion. It is a hard, rigorously scientific fact. Nor, do I gloat over the sad condition into which so many among my fellow-humans have been plunged by today's popular culture. My purpose here is not to dissect a corpse, but to cure the living of a potentially fatal mental illness. The timeliness of my exertion to this latter purpose, is located in my certainty that the "Pearl Harbor-like" effects of the ongoing disintegration of the present international financial and monetary systems, can be employed to an effect akin to the anti-Windsor effect of the murder of Princess Diana, as a "reality shock," to reverse the youth-countercultural revolution of the mid-1960's, to shock today's fantasy-ridden "Baby Boomer" and "X" generations into a sense of reality.
Yes, during the Truman years, there was cultural decay among a fairly estimated ninety-five percent of the returning veterans of World War II. The reliance on search for truth went out the window, replaced by a compelling sense of the importance of "political correctness" in choosing mate, career, and opinions expressed in public, or even in the privacy of the bedroom.
However, during the 1946-1966 years, among university populations (in particular), the form of corruption common among campus beneficiaries of the "G.I. Bill of Rights," was typified by concern to earn the degrees which would gain well-paid and prestigious careers within a society still dominated by a cultural orientation toward investment in the benefits of scientific and technological progress. Education became, more and more, a pursuit of the popular, erotic notions of what current opinion acknowledged as prestige and family financial security, without the distracting, often contrary burden of searching for truth.
Unfortunately, most of those students (and their professors) were morally corrupted, in the sense of Jena Professor of History Friedrich Schiller's famous concept of the Brotgelehrte: in my free translation, "people who are trained to sing for their suppers, not for the sake of music." During the Truman, Eisenhower, and Kennedy years, the cultural "status" still enjoyed by the idea of "benefits of scientific and technological progress," fostered a shadowy approximation of respect for truthfulness, in the guise of occasional expressions of respect for the general idea of scientific and analogous rationality.4
That was no longer true after the takeover of the minds of the majority of "Baby Boomers," under the influence of the anti-science virus embedded in the core-belief of the true believer in "post-industrial" utopianisms. For relevant, affected strata of "Baby Boomers," that "cultural-paradigm shift" removed all semblance of governance of behavior by notions of some absolute obligation to considerations of rationality and morality. Morality was replaced by "Ethics," in the sense of "politically correct" agreements among persons of mutually irreconcilable principles and factual belief. The "ethics" of the variously so-called "therapy," "encounter," or "sensitivity" group, became the hegemonic substitute for morality and reason within the ideological core of the "Baby Boomer" generation. Thus, that ration of that stratum, may sometimes be better described as the "Baby Boomer degeneration."
A study of history shows, that a properly crafted approach to innoculating "Baby Boomers" and others against the potentially negative effects of the oncoming "reality shock," is the only tactic by means of which this cultural degeneration might be abruptly reversed, and this civilization thus rescued from what would be, otherwise, its "lemming-like" plunge into self-induced, inevitable doom.
The first step is to diagnose the illness: to identify the relevant symptoms, and to track these disabling symptoms to their causes. To that purpose, the first steps examine the most relevant symptoms as expressed in three domains: music, literature, and the issues of the centuries-long dispute, since Johannes Kepler, over the mathematical calculus. The second, final step, is to show the commonly underlying source of these three classes of symptoms.
The Case of Wilhelm Furtwängler
The leading figure of Twentieth-century musical life is the celebrated conductor Wilhelm Furtwängler. All the other great ones of this century, such as Pablo Casals, for example, have been co-thinkers of Furtwängler's practice respecting the performance of music. Furtwängler's use of the descriptive expression, "performing between the notes," or "performing from behind the notes," points our attention directly to the crucial issue of all Classical musical performance, and, implicitly, to such other expressions of great Classical art as are to be found in literature, and in Classical forms of plastic arts from Scopas and Praxiteles, through Leonardo da Vinci, Raphael Sanzio, and Rembrandt. It is also the fundamental principle of science, as science was defined by Plato and his Academy, by Nicolaus of Cusa, and by such outstanding followers of Cusa's founding of modern physical science as Luca Pacioli, Leonardo, Johannes Kepler, Gottfried Leibniz, Carl Gauss, and Bernhard Riemann.
In short, for all competent Classical musicians,5 the performance of music is not the "interpretive performance" of the notes on the written musical score. Those notes are no more than the poor, linear footsteps, left behind in the pale sand of the score, left by the being which had first walked there. As Furtwängler emphasized, in various statements on this matter: a great musical composition, as reflected by such footsteps, is the product of a cognitive, creative process which occurred within the mind of the composer. He emphasized, repeatedly, that the task of the performing musician, is to relive the process of cognition by which that composer generated that composition. I echo him, thus, in insisting on the principle, that although the performer must walk in that composer's footsteps, using the specific notes and other indications supplied by the composer, it is the performer's (and, also the audience's) reliving of those processes which occurred within the mind of the composer, the which must govern the performance of those notes, rather than a stylized interpretation of those mere notes as such.
To perform Wolfgang Mozart's work, you must gain not only technical performing skills, but you must also recapture within your own mind, the way in which Mozart thought, within the privacy of his own, sovereign cognitive processes of musical composition. You must relive being Mozart, in the same sense that one can know a principle of nature, only by reliving the sovereign cognitive processes mustered by the original discoverer of that principle. This will be made clearer at relevant later junctures in this report.
In order to reconstruct the composer's process of composition, the performing artist must locate the composer, functionally, within the actual historical setting in which the composer had lived and worked. Thus, the early composition of a Josef Haydn was situated historically, chiefly, in the intersection of the reflected influence of Johann Sebastian Bach, as reflected through the influence of Carl Phillip Emmanuel Bach's work, upon Haydn's native, Italian-influenced, South German musical tradition of the middle Eighteenth century. Wolfgang Mozart's work was strongly influenced, earlier, by the two Haydn brothers, and, beginning the early 1780's, by intensive study of the well-tempered polyphonic methods of J.S. Bach. Beethoven was situated, chiefly, in that modification of the Italian tradition imposed by J.S. Bach, Haydn, and Mozart. The work of all Nineteenth-century Classical composers, including Schubert, Mendelssohn, Schumann, and Brahms, is permeated by the overreaching influence of Bach, Haydn, Mozart, and Beethoven. Even Romantic opponents of the Classical method, such as Franz Liszt, or Hugo Wolf, parodied the Classical tradition at the same time that they expressed their intent to reject it.
Notably, beginning with his compositions centered around the six "Haydn Quartets," Wolfgang Mozart used his higher comprehension of the implications of J.S. Bach's A Musical Offering (and, at least, implicitly, also Bach's The Art of the Fugue), to establish a new method of composition, known, generically, today, as Classical motivic thorough-composition. As former Primarius of the Amadeus Quartet, Norbert Brainin, discovered, some decades ago, Mozart's dedication of that set of six quartets to Josef Haydn, reflects a specific debt to Haydn, Haydn's pioneering of a method of motivic composition in his own, six "Russian Quartets," Opus 33. In musicology, almost the entirety of the leading work of Beethoven, some of the work of Schubert, of Schumann, and, most notably, Brahms, continues a tradition of motivic thorough-composition typified, in germ-form, by Mozart's Köchel 475 Fantasy on Bach's A Musical Offering.
Thus, to approach the performance of any Classical composition, from Haydn through Brahms (most notably), one must read Bach's establishment and development of well-tempered polyphony, as Mozart, Beethoven, and others traced the method of motivic thorough-composition to its origins in Bach. The first task of the performing artist, is to become steeped in that work of two centuries, to have relived, in the performer's own mind, the succession of musical-compositional discoveries which each composer represented in respect to his, or (e.g., Clara Schumann) her predecessors. Each composition must be reexperienced by the performing artist from that standpoint. Each composition, so historically situated in that way, must be reexperienced, as a process of composition, within the mind of the performing artist.
Compare this case, for music, with my use of Riemann's 1854 habilitation dissertation6 as a point of reference, for describing the mental processes by means of which a validatable original discovery of physical principle is generated within the same, sovereign cognitive processes of the individual mind.
How Leibniz's Calculus Is Untaught
For our purposes here, it is useful to recapitulate what I have stated in numerous earlier locations as a defense of Leibniz's calculus against the usually accepted classroom misrepresentation of that calculus, as supplied by Augustin Cauchy. The hoax of linearization in the small, as argued by Antonio Conti's Dr. Samuel "Samiel" Clarke,7 as restated, more rigorously, by Leonhard Euler, by Cauchy, and others, expresses the same pathological state of mind in mathematical ideas about physical science, as the defective mental condition of those celebrated musicians whose methods Furtwängler opposed.
Bernhard Riemann's essential significance in the history of science, is, that he was the first to liberate mankind from a deluded, Aristotelean interpretation of Euclid's geometry.8 Riemann, basing himself most immediately on Carl Gauss's implicitly "non-Euclidean" development of a general theory of curved surfaces,9 defined every validated principle of nature as having the function, within a general notion of physical-space-time manifolds, of a "dimension" in Euclidean geometry. Implicitly, the ideas of space and time, themselves, existed for Riemannian physics solely as experimentally validated principles of physical space-time, rather than as "self-evident," axiomatic presumptions.10
Furthermore, Riemann argues, that, although such discovered, and experimentally validated principles had a certain independence from one another (hence "dimensions"), one could not adduce the internal metrical qualities of physical space-time merely from those "dimensions" themselves. One must take into account the fact, that the metrical characteristics of any physical space-time manifold are themselves the subject of experimental determination.11 That latter notion, of such a metrical characteristic, is the notion of curvature, as curvature attains its metaphorical expression in the higher reaches of the extended orders of hypergeometries envisaged in the relevant work of Gauss and Riemann. In other words, the interaction among the "dimensions" of a physical space-time manifold is expressed, in metrical terms, as the experimentally established Gauss-Riemann curvature characteristic of action which is internal to that manifold.
That takes us back to Johannes Kepler, as well as to the interrelated notions of Analysis Situs, and of the families of catenary-like curvatures, as both were presented by Leibniz. Our focus here, should be upon the grounds Kepler proposed to future mathematicians, the development of what became Leibniz's calculus. Our attention is also referenced to Vol. VI of the collected works of Carl Gauss, on the subject of astrophysics, specifically Gauss's unique success, beginning 1801-1802, in determining the orbits of the then recently-discovered asteroids. To keep the argument as simple as possible, begin with this discovery of those orbits by Gauss.
The historical setting, and the immediate facts of the matter, are presented in rather full detail, for the benefit of the reader who would wish to check the present writer's reading from those sources: in the published Carl Gauss Werke, the associated, published, collections of Gauss's correspondence, and a rather rich supplementary literature, including relevant primary sources presented. With those assurances supplied, we summarize the particular case in the manner and degree needed to indicate the relevant, crucial point under consideration at this moment.
Gauss's calculations of the orbits of the relevant, then just recently observed astronomical bodies was Gauss's first notable application to physics of the revolutionary methods he had featured within his ground-breaking Disquisitiones Arithmeticae.12
The principle which Gauss applied was that set forth by Johannes Kepler: the lawfully determined trajectories of motion in physical space-time must be understood as reflecting some universal physical principle which is as much manifest in the smallest conceivable interval of that trajectory, as in the large. Kepler's concern to this effect was heightened by his concern with the fact that the orbits of the planets were elliptical, rather than circular. That concern pointed to the importance of our ability to measure non-constant curvature, even in observations of very small intervals of the trajectories. For this, Kepler proposed that future mathematicians develop a calculus capable of addressing the problems of measuring non- constant curvature of extremely small intervals of action.
This had led Leibniz to his intial, 1672-1676 successes in developing an integral and differential calculus, as reflected both in the work he submitted to a Paris publisher, in 1676, and in the surviving manuscripts of his work in this subject-area, in the Hannover archive, from the 1672-1676 interval. In the context of Kepler's concern: given, a non-linear curvature within an infinitesimally small interval of a trajectory, how might we measure that curvature, and how might we integrate a complete trajectory (e.g., orbit) from that measurement?
This is the characteristic difference, which shows that Newton's work provides no calculus at all, not even a defective one. This is also the characteristic difference, which points to the axiomatically fraudulent assumptions underlying Cauchy's well-known derivative fraction.
Gauss applied this Kepler-Leibniz principle of the calculus, as he himself had addressed the relevant conceptual problems of an experimental mathematical physics in his Disquisitiones. This led to Gauss's remarkable success, in surpassing everyone else in the only successful adducing of the orbit of Ceres from the same array of observational data employed by others in the same period. Whereas the others relied upon what we would fairly describe as curve-fitting approaches to an array of observed points, Gauss concentrated on finding several intervals of observation which had the same curvature, and extrapolating from that congruence to project the entirety of the relevant Keplerian orbit with the harmonic characteristics which Kepler had prescribed for a missing planet in a specified orbit between those of Mars and Jupiter.
At this point, the reader should be informed that these considerations, pertaining to the dispute over the axiomatic underpinnings of a calculus, have a distinct, decisive relevance for competent understanding of the musical principle cited by Furtwängler. Once this point is grasped, it is feasible to render transparent those specific, cognitive characteristics of the mental-creative processes of the individual person which are the place of generation of all validatable discoveries of physical principle, and all valid expressions of composition and performance of Classical works of music, poetry, drama, and plastic art-forms. On that account, the writer is accountable for his making a credible effort to identify that relevant aspect of the issue of the calculus even to the proverbial "non-mathematical" reader.
To that latter purpose, I borrow an illustration presented by my colleague Dr. Jonathan Tennenbaum, a problem he presented as a challenge to the audience, during a recent, summer conference at Oberwesel, Germany.13 From the standpoint of an observer at a fixed point on the surface of the Earth, the sun appears to make a daily, circular orbit of the Earth. Yet, by means of observation from the surface of the Earth, it has been known for nearly 2,500 years (at least) that the Earth orbits the sun, an orbit which we known to be elliptical, as Kepler has already shown us. Therefore, solve this paradoxical juxtaposition of circular and ellipitical orbitting.14
Place a circle, representing the apparent daily orbitting of the Earth by the sun, such that the circle's center is initially placed at the insection of a two-dimensional, Cartesian graph. Let the "Y" axis represent the position of the sun in that orbit, and the "X" axis, time. Thus, the apparent rotation of the sun around the Earth will generate the image of a Cycloid. [see: Figure 1] However, the position of the observer on Earth is changing relative to the Earth's orbitting an elliptical pathway around the sun. Thus, the cycloid generated is not a simple cycloid, but a quasi-cycloid (called an "epi-cycloid"), which rolls along the elliptical orbit, rather than a Cartesian straight line. [see: Figure 2]
The images of space-time determined by the geometric products of cycloid and conic sections bring us into the domain of the famous curve known as a catenary, and of related functions. If we continue in this direction, into Riemann's revolutionary principle of physical space-time,15 we depart the domain of Euclidean notions entirely, into the domain known as hypergeometric functions. In this domain, from the catenary into still higher geometrical cardinalities, the Cauchy theorem (e.g., "fraction") has no existing correspondence to reality.16
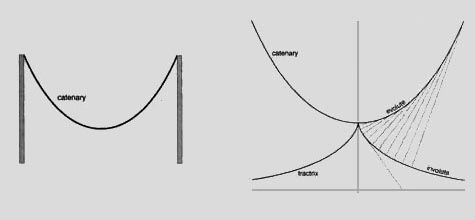
Notable, is Leibniz's extensive attention to the implications of René Descartes' refusal to accept the existence of the catenary. [see: Figure 6] For our purposes here, to show Leibniz as a follower of Kepler and forerunner of those notions of hypergeometry presented by Gauss and Riemann which are relevant for the subject of our present paper, it is sufficient to excerpt the Loemker edition's translation of two citations from Leibniz himself:
 |
||||
| FIGURE 6. A catenary is the curve formed by suspending a rope between two points. The endpoint of a taut thread unwound on a catenary, traces out a curve called a “tractric.” The perpendiculars to the tractric are tancent to, and envoloop, the catenary; this is called an involute-evolute relationship in geometry. |
||||
Besides quantity, figure in general includes also quality or form. And, as those figures which are equal whose magnitude is the same, so those are similiar whose form is the same. The theory of similarities or of forms, lies beyond mathematics and must be sought in metaphysics [e.g., metamathematics, hypergeometry—LHL]. Yet, this has many uses in mathematics also, being of use even in the algebraic calculus itself. But, similarity is seen best of all in situations or figures of geometry. Thus, a true geometric analysis ought not only consider equalities and proportions which are truly reducible to equalities, but, also, similarities and, arising from the combination of equality and similarity, congruences.17As Kepler emphasized, the planetary orbits are forms whose similarities, including self-similarities, reside in the forms themselves, forms associated, dependently, with both position, and with the species of harmonic characteristics defined by Kepler's treatment of both observed, and unobservable orbits. Crucial is the case of the orbital characteristics which Kepler calculated for that which Gauss measured, approximately two centuries later, for asteroid fragments of a missing planet. Kepler derived this necessary orbit for a missing, exploded planet from a principle of formal similarities, exactly as Leibniz defined Analysis Situs. Thus, Gauss's success, achieved by Gauss's choice of method, represents a devastatingly crucial experimental proof-of-principle, supporting Kepler's and Leibniz's conception of a calculus, against the method of Descartes and of empiricists such as Newton, Clarke, Euler, and Cauchy.... It is a very true and indubitable law of nature, that the same thing, so far as in it lies (always persists in the same state) ... a law which both Galileo and Gassendi, and some others as well, have long held. ... [N]ot only did Kepler observe the very beautiful law of nature, according to which bodies describing a circular or curved path strive to leave it in the line of the tangent straight line (others may have preceded him in this), but, he already made clear that application of this law which I consider essential in making clear the cause of gravity. This is apparent from his Epitome of the Copernican Astonomy. ... 18
In summary of that particular argument, the facts to be considered, are principally two.
More simply, in physical space-time, there exist trajectories, whose characteristic metrical qualities are non-constant (e.g., non-linear) in the extremely small interval, such as the infinitesimal. Small as it may be, the curvature in the infinitesimal is similar to the curvature of the trajectory as a whole. Thus, the presumption of the Cauchy fraction, while convenient for purposes of engineering calculations, where no issue of principle is involved, is absurd relative to a calculus suited to proof-of-principle arguments respecting physical reality.19 The notion of "linearization in the small," as proposed by Clarke, Euler, Cauchy, and others, can not be supported.
More deeply, in the exemplary case of planetary orbits, we are dealing with phenomena which are repetitive over the relatively longer term, such as thousands of years. Looking into those orbits more deeply, we find that the changes in characteristics of the orbits appear to be repetitive, in terms of tens of thousands, hundreds of thousands, or millions of years. Such hierarchies of repetitiveness appear to us as suggesting "laws of the universe," patterns of similarity which, in fair approximation, lie outside the reach of any ordinary action among particular objects; indeed, it appears that these patterns of similarity subsume, in the sense of bounding, the allowed possibilities for inter-action among particular objects within the system. Planetary orbits, and recurring patterns in observed stellar constellations, have long exemplified this case.
Thus, Leibniz's allusion to the term "metaphysics." Like Dr. Tennenbaum's referenced example, the concentric (i.e., hypergeometric) trajectories defined by such very long cycles within the solar system, represent a continuing principle of action. This principle, we associate with the most inclusive, long-term component we can adduce, as we situate the apparently circular, daily, cycloidic orbitting of the sun, around the Earth, with the superior, elliptical, annual orbitting of the Earth around the sun. As in the case of the small aberrations which the solar cycle imposes upon each infinitesimal interval of the daily apparent orbit of the sun, so, the longest solar, galactic cycles must be manifest as curvature within the smallest interval of all observed events. That difference in curvature within the infinitesimal, thus reflects the true trajectory of our solar system, our galaxy, over even billions of years. That difference, rightly adduced, contains the key to the trajectories of the relevant portion of the universe over the relevant very long time, up to the point we can introduce further such alteration in the relevant concatenation of principle.
Hence, Leibniz's insistence upon "non-constant curvature" as a standard of reference for measurements within the infinitesimally small. Hence, Gauss's stunning success, in contrast to his ostensible competitors, in defining the Keplerian harmonic characteristics of the orbit of Ceres.
The presently "politically correct" standard of the mathematics classroom, the well-trodden pathway of linearization in the infinitesimally small, the notion of Clarke, Euler, Cauchy, et al., thus becomes a pseudo-scientific absurdity, the instant we depart from the practice of consideration of nearness to zero as a crude, but useful engineering approximation, into attempting to define physical principles according to such crudities. The further into astrophysics, and into time, we extend our inquiries, the more refined our conception of universal principle must be; similarly, the more we penetrate into regions of smallness previously unexplored.
The case of Descartes' silliness, in denying the existence of the catenary curve, is relevant. In contrast to Leonardo da Vinci, who discovered the catenary/caustic phenomenon of natural principle, Descartes is an Aristotelean (or, to quibble, a neo-Aristotelean), who argues from the naive reading of a Euclidean geometry of space-time, and, therefore, excludes, even hysterically, everything which can not be derived from that in a simple-minded, deductive way.20 Leonardo, his follower Kepler, Leibniz, Gauss, and Riemann, insist that reality is located in a non-Aristotelean, Platonic reality, a universe which man knows through the success of man's creative cognitive powers in discovering validatable principles through which mankind's power over the universe is willfully increased. In other words, physical laws are products of those qualities of individual mental activity which generate those newly discovered principles, by means of which the universe's submissiveness to the human will is increased. In other words, the universe was predesigned to submit only to those qualities of the individual human mind which express natural law, those qualities of cognitive potential which define every man and woman as not as oligarchical and other evil society defines slaves and serfs, as "wretches," not "worms" before the throne of some pagan's "Emperor God," but as beings whose essential goodness is that they are "made in the image of God."
This is a notion which escaped the comprehension of the slyly contemplative oligarchical lackey, Aristotle, and of those submissive mentalities which follow Aristotle in such an oligarchical, licky-lackey-like tradition.
So much said, thus far, the time has come to turn to the mental processes, located behind the opaque screen of sovereignty of the individual person's cognitive processes, processes by means of which validatable discoveries of physical principle are effected, as they can not be effected by any alternate means. It is in those mental processes, that the secret of our ability to discover the laws of the universe is lodged. Thus, the precondition for scientific truthfulness, is the rigorous exploration of those mental processes, by means of which validatable discoveries of principle are achieved. Therein lies the essence of the Classical principle of art and science.
|
Footnotes |
||
1. Barbara Tuchman, A Distant Mirror: The Calamitous Fourteenth century (New York: Alfred A. Knopf, 1978).
2. President Lyndon Johnson's sponsorship of two civil-rights bills typifies this generational character. Many among those who had come to adulthood under the leadership of President Franklin Roosevelt, had experienced a reactivation of the American patriotic heritage of Franklin and Lincoln; in later years, however reluctantly, sometimes this represented a moral impulse within them which they found it difficult to resist. For the most part, that quality of moral impulse vanished with the impact of the 1964-1970 countercultural takeover of the " '68ers' " generation.
3. Although these events triggered the susceptibility for the wildfire spread of the "youth counterculture" of the middle to late 1960's, a thorough treatment of that pathological effect must not overlook the powerful, cumulative impact upon suggestible young minds of "mind wars" indoctrination of the population, during the interval from approximately 1951, into the 1975 collapse of the government of South Vietnam. Without the "mind wars" indoctrination of the population, as led by the London Tavistock Clinic and Institute, and coordinated through the U.S. networks of Britain's Brigadier Dr. John Rawlings Rees, Eric Trist, the circles of Dr. Kurt Lewin, and by the Tavistock-connected networks of the so-called "Frankfurt School," the campus "Baby Boomers" of the middle to late 1960's could not have been brainwashed into adopting the specific type of "rock-drug-sex youth counterculture."
4. This was complicated by the influence of H.G. Wells and Bertrand Russell, as typified by the radical nominalist (e.g., William of Ockham) spread through channels such as the utopian, sociology-dominated "science fiction" fads, especially those of the past fifty years. The "Ozone Hole" hoax of F. Sherwood Rowland typifies the degree to which the practice of the Occamite positivism of Bertrand Russell clones Norbert Wiener and John Von Neumann had degenerated by the early 1970's.
5. The use of the term "Classical" here signifies not merely the Classical literature, as from J. S. Bach through Brahms, but other music which satisfies the standard of the Classical principle, as Haydn, Beethoven, Brahms, and Brahms' protege Dvorak addressed the Classical potential of certain actual, or potential qualities of folk-song. "Classical" is employed, thus, in the sense of rejection of such forms of degeneration into eroticism expressed by Romantics such as Claudio Monteverdi and Franz Liszt, and the Modernist, Post-Modernist, and the satanic fad inhering in both the rythms and lyrics of "rock." Respecting "Modernists" and "Post-Modernists," to raise the issue of competence, is comparable to debating the artistic qualities of smell exuded by ripe garbage.
6. Bernhard Riemann, Über die Hypothesen, welche der Geometrie zu Grunde liegen, paragraphs 1 and 2, in Bernhard Riemanns Gesammelte Mathematische Werke, ed. by H. Weber (New York: Dover Publications reprint, 1953). Hereinafter identified as [Riemann: Werke].
7. See, "The Controversy Between Leibniz and Clarke," in Gottfried Wilhelm Leibniz: Philosophical Papers and Letters, ed. by Leroy M. Loemker (Dodrecht, Netherlands: Kluwer Academic Publishers, 1989), pp. 675-721. Dr. Clarke was Isaac Newton's controller, acting for the relevant chief of Venice's foreign-intelligence service at time, the same Paris-based Abbot Antonio Conti (1677-1749), who deployed Voltaire, Physiocrats such as Franc@acois Quesnay, and such Leibniz-haters of Frederick II's Berlin Academy as Pierre-Louis Maupertuis and Leonhard Euler. It was Conti who invented the Isaac Newton of today's popular legends. Newton's own scientific accomplishments were relatively trivial, as John Maynard Keynes has documented the reality of the long-mysterious chest of Newton papers. [See "Newton the Man," in Newton Tercentenary Celebration (Cambridge: Cambridge University Press, 1947), pp. 27-34.] The work often attributed to Newton was done by other associates of the London Royal Society. Newton's unworkable parody of Leibniz's 1676 version of the calculus, is typical. It was the Conti network's Leonhard Euler who later set forth Clarke's argument on the calculus in the form copied by "Cauchy's fraction."
8. Ibid., p. 272.
9. Ibid. See also, Carl Friedrich Gauss Werke ["Werke"], in 12 volumes, plus correspondence (Hildesheim-New York: Georg Olms Verlag, 1981): Theoria residuorum biquadraticorum, I (1828) and II (1832), Vol. II, pp. 65-148; Allgeimeine Aufösung der Aufgabe die Theile einer gegebenen Fläche so abzubilden, dass die Abbildung dem Abgebildeten in den kleinsten Theilen änlich wird (1822: Copenhagen Prize Essay), Vol. IV, pp.189-216; Disquisitiones generales circa superficies curvas (1828), Vol. IV, pp.217-258. The subject-matter of the latter two Gauss papers (the necessary, non-linear self-similarity of the trajectory of lawful processes in the infinitesimally small, to the same trajectory in the large) is of crucial significance respecting Gauss's original solutions for the orbits of the asteroids Ceres and Pallas [Werke, Vol. VI], and for appreciating the physical implications of the axiomatic difference between the original Leibniz calculus and the bowdlerized version of it (e.g., the "limit theorem," or "Cauchy's fraction") popularized by the notorious plagiarist, Leibniz-hater, and political and scientific adversary of the Ecole Polytechnique's Gaspard Monge, Augustin Cauchy.
10. Riemann, ibid.
11. "Es muss also entweder das dem Raume zu Grunde liegende Wirkliche eine discrete Mannigfaltigkeit bilden, oder der Grund der Massverhältnisse ausserhalb, in darauf wirkenden bindenden Kräften gesucht werden," Riemann, op. cit., p. 286. In that context, "continuous manifold," as distinct from "discrete," refers to a process determined by a continous principle of action, whether or not the affected interrelations among the phenomena within that manifold are themselves continuous or discrete in form. Such continuous processes lie, ontologically, in the domain which Plato identified as "higher hypothesis," which corresponds to Leibniz's usage of the term "Analysis Situs."
12. (Leipzig: 1801) The republication of the original, Latin edition of this extraordinary work occupies Vol. I of the Werke. There are good German and English editions extant. A good modern education in mathematics and physics would feature the student's reworking of this Gauss work as a central, and controlling feature of the combined secondary and undergraduate education in scientific method. This work either reflects the leading work of Gauss's predecessors, since Classical Greece, or serves as a most convenient pedagogical benchmark, by aid of which the work of Gauss's predecessors may be brought into focus for critical understanding of the leading issues of modern scientific practice.
13. When a member of that audience challenged me, after Dr. Tennenbaum's address, to solve the paradox, I declined to do so, for reasons I expained at that time. He had presented this as one of a series of paradoxes, which the individual members of the audience must solve by their own powers. I limited myself to restating the same paradox in my own preferred terms, indicating that the solutions to my own and Dr. Tennenbaum's formulation of the case would be identical.
14. This was already known during the Third century b.c.: , centuries prior to the willful hoax perpetrated by Claudius Ptolemy. There was never an honest reason for any authoritative institution, in the Roman Empire, or later, to believe that the sun orbitted the Earth.
15. Riemann, op. cit.
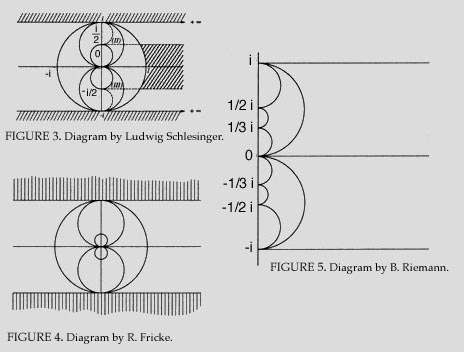
16. Relevant is Gauss's introduction of his students to the domain of hypergeometry, as reported by Ludwig Schlesinger [Werke X, 2, p. 102] [see: Figure 3], also by R. Fricke [Werke VIII, p. 103] [see: Figure 4], and Riemann's related representations, such as a figure he supplied as part of his Vorlesungen über die hypergeometrische Reihe, [Werke, Appendix, p. 93] [see: Figure 5].
 |
||||
| In his work on the arithmetic-geometric mean and hypergeometirc functions, Gauss invented what became known as the “modular diagram,” which portrays the internal relationships among entire families of functions, as defined by their underlying geometrical characteristic (“modulus”). Each locus represents a family of functions with a common modulus: these families are related to each other by transformations which “map” the indicated regions onto each other in a “conformal” manner. |
||||
17. Loemker, op. cit.: "On Analysis Situs," from pp. 254-255. [I have added necessary corrections to the translator's punctuation, resisting temptation to supply other improvements—LHL.]
18. Op. cit., p. 395. [Some puncutation supplied—LHL.]
19. E.g., Riemann, op. cit., "III. Anwendung auf den Raum," pp. 283-286.
20. The development of the concept of the catenary, and its relationship to the tractrix, was initiated by Leonardo da Vinci, but its modern elaboration was chiefly the work of Christiaan Huyghens and Gottfried Leibniz, during the latter decades of the Seventeenth century. (Cf. Christiaan Huyghens, The Pendulum Clock, trans. by Richard J, Blackwell (Ames, Iowa: Iowa State University Press, 1986), Parts II and III.) The issue of the catenary was among the several principal foci of Leibniz's demonstration of the essential incompetence of the methods of René Descartes and Isaac Newton.
Fidelio Table of Contents from 1992-1996
Fidelio Table of Contents from 1997-2001
Fidelio Table of Contents from 2002-present
Beautiful Front Covers of Fidelio Magazine
What is the Schiller Institute?

Join the Schiller Institute,
and help make a new, golden Renaissance!
MOST BACK ISSUES ARE STILL AVAILABLE! One hundred pages in each issue, of groundbreaking original research on philosophy, history, music, classical culture, news, translations, and reviews. Individual copies, while they last, are $5.00 each plus shipping
Subscribe to Fidelio:
Only $20 for 4 issues, $40 for 8 issues.
Overseas subscriptions: $40 for 4 issues.
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
schiller@schillerinstitute.org
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps |
Dialogue of Cultures
© Copyright Schiller Institute, Inc. 2001- 2003 All Rights Reserved.

