Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps
Dialogue of Cultures
 |
||||
| Carl Friedrich Gauss: Under what curvature (modulus) are the relations between objects congruent? | ||||
|
PEDAGOGICAL EXERCISE
|
The Epinomis and the Complex Domain:
A Fragmentary Dialogue in the Simultaneity of Eternity
For related articles, scroll down or click here.
The Epinomis and the Complex Domain:
A Fragmentary Dialogue in the Simultaneity of Eternity
Plato’s dialogue of the Laws, continues in the short appendix known as the Epinomis,* written most likely not by Plato himself, but by the student Philip of Opus, who is also said to have “transcribed” the Laws from the wax tablets left unfinished by Plato at the time of his death. Speaking is the Athenian visitor, the primary interloculator of the Laws:
“Of all the sciences that now exist, which one would render humans the most unintelligent and senseless of living things, if it completely disappeared from the human race or had not been developed? In point of fact, it is not at all hard to identify. If we compare, so to speak, one science with another, we will see that the one that has given the gift of number would have this effect upon the entire mortal race. ...
“ ... [W]e were very right to observe that if the human race were deprived of number, we would never come to be intelligent in anything. We would be animals unable to give a rational account [logos], and our soul would never obtain the whole of virtue. An animal that does not know two and three, or odd and even, one that is completely ignorant of number, could never give an account of the things it has grasped by the only means available to it—perception and memory. But while nothing prevents it from possessing the remainder of virtue—courage and moderation—no one deprived of the ability to give a true account can ever become wise, and anyone lacking wisdom, which is the greatest part of all virtue, can never become completely good or, in consequence, happy. Thus, it is altogether necessary to employ number as a basis, though why this is necessary would require a still longer account than all I have said. But we will also be right in stating the present point, that regarding the achievements attributed to the other arts [technical skills; not liberal or fine arts], the ones we recently surveyed when we allowed all the arts to exist, not a single one remains. They are all completely eliminated when we take away the science of number.
‘The Gererated World’
“If we reflect upon the arts, we might well supposed that there are a few purposes for which the human race needs numbers—although even this concession is important. Further, if we contemplate the divine and the mortal elements in the generated world [genesis: creation], we will discover reverence for the divine and also number in its true nature. ...
“ ... How did we learn to count? How did we come to have the concepts of one and two? The Universe has endowed us with the natural capacity to have concepts, whereas many other living things lack even the capacity to learn from the Father how to count. With us humans, the first thing God caused to dwell in us was the capability to understnad what we are shown, and then he proceeded to show us, and he still does. And, of the things he shows us, taken one by one, what can we behold more beautiful than the day? Later, when we come to see the night, everything appears different to our vision. Since Heaven [the god Ouranos: ] never stops making these bodies ply their course night after night and day after day, he never stops teaching humans one and two, until even the slowest person learns well enough to count. For each of us who sees them will also form the concepts of three, four, and many. Out of these many, God made a unit by constructing a moon which goes through its course, sometimes appearing larger and sometimes smaller, thus always revealing each day as different, until fifteen days and nights have passed. This is a period, if one is willing to treat the entire cycle as a unit. As a result, even the stupidest of the animals God has endowed with the ability to learn, is able to learn it. ... [A]fter creating the moon, waxing and waning as we said, God established months in relation to the year, and so all the living beings who could, began to comprehend number in relation to number [i.e., ratio and proportion], with the blessing of Good Fortune. Thanks to these celestial events we have crops, the earth bears food for all living things, and the winds blow and the rains that fall are not violent or without measure. If, on the contrary, anything turns out for the worse, we must not blame God, but humans, for not rightly managing their own lives. ...
“I must try, then, to give a detailed account of ... what things a person is to learn about reverence towards the gods, and how he is to learn them. When you hear what it is, you will find it strange. I say its name is astronomy, an answer no one would ever expect, through unfamiliarity with the subject. People do not know that the true astronomer must be the wisest person. I do not mean anyone practicing astronomy, the way Hesiod did, and everyone else of that sort, by observing risings and settings of stars, but the one who has observed seven of the eight circuits [the orbits of the sun, moon, and planets Mercury, Venus, Mars, Jupiter, and Saturn; the eighth, that of the celestial sphere, carries the daily motion of the others, creating day and night], each of them completing its own orbit in a way no one can easily contemplate who is not endowed with an extraordinary nature. We have now said what we must learn. We shall go on to state, as we say, how we must and should learn it. My first point is the following.
“The moon completes its circuit most quickly, bringing the month [the new moon] and before it the full moon. Next we must attain knowledge of the sun, which brings the solstices as it completes its entire circuit, and the planets that accompany it [i.e., Venus and Mercury]. To avoid repeating ourselves many times about the same things, since the remaining orbits which we discussed earlier are not easy to understand, we should make continuous efforts in preparing for this knowledge the people whose natures can understand it, to teach them many preliminary subjects and accustom them to learning when they are boys and youths. For this reason, they need to study mathematics [mathematon: the mathematical sciences].
“First and foremost is the study of numbers in their own right, as opposed to numbers that possess bodies. This is the study of the entire nature and properties of odd and even—all that number contributes to the nature of existing things. After learning this, next in order is what goes by the extremely silly name of geometry [geometria] [literally, “earth measurement”]. In fact, it is absolutely clear that this subject is the assimilation by reference to plane surfaces of numbers that are not by nature similar to one another [i.e., species differences: incommensurables].”
Plato presents the irony, of a connection between the study of “numbers in their own right, as opposed to numbers that possess bodies,” and the mastery, in the mind, of the motion of the heavenly bodies—astronomy. Previous investigations† into linear, polygonal, and geometric numbers, and Carl Gauss’s work on the calendar, show this connection is in the realm of Higher Arithmetic, which was Gauss’s re-working of classical science.
In our previous studies, we quickly learned the foolishness of thinking of numbers in connection with objects or bodies. Instead, we began to discover that knowledge lies in investigating the relations between numbers, not the numbers themselves. We discovered how to begin to distinguish these relations as different types of differences (change) among numbers. Numbers, related to one another by the same type of difference, are congruent relative to that type (modulus). These types of differences, can be distinguished from one another, either by magnitudes, as in the case of linear and polygonal numbers, or by incommensurability, as in the case of geometric numbers. As we discovered with Gauss’s application of Higher Arithmetic to the determination of the Easter date, when the mind abandons all foolish fixation on objects, and focusses instead on the relations between them, an extremely complex many, can be brought into our conceptual ken as a unity. [See Box]
A similar approach can be taken with respect to astronomy. As the Epinomis indicates, nothing can be discovered about the astrophysical by simple observations, like the methods of Hesiod. Instead, one must look to the type of change (relations), of which those observations are merely a reflection.
Think of two objects, representing two observations of a planet in the sky. What is the relationship between these two objects? What one must investigate, is the type of difference (change) between those objects. Or, under what curvature (modulus) are the relations between these objects congruent?
For example, if those two objects are related to each other by a straight line, then the type of difference is measured by rectilinear action, no matter how small the interval between them. If, however, they are related to one another by a circular arc, the type of difference will be characterized by constant curvature, not rectilinear action, no matter how small the interval between them. Or, if they are related by an elliptical arc, the type of difference is characterized by changing curvature, no matter how small the interval between them. The mind must distinguish the type of change: rectilinear, constant curvature, changing curvature, or types of changing curvature. The determination of which type of change is related to these specific observations; it is not a formal question, but a matter of discovery.
By the time he was sixteen or seventeen years old, Gauss had already discovered a new type of difference—congruence in the complex domain—which he applied to his work throughout his life. Not until thirty-seven years later, in his second treatise on biquadratic residues, did Gauss begin to elaborate the metaphysical principles behind this discovery.
We can gain some insight into Gauss’s thinking, from the following fragment, taken from one of his 1809 notebooks:
Questions Pertaining to the Metaphysics of Mathematics
1.
Which is the essential condition, for a connected array of concepts to be thought of in relation to one magnitude?
2.
Everything becomes much simpler, if at first we abstract from the infinity of divisibility, and consider merely discrete magnitudes. For example, as in the biquadratic residues, points as objects, as transitions, and hence relations as magnitudes, where the meaning of a + bi − c − di is immediately clear. [This is accompanied by a drawing a grid in the complex domain; See Figure 3—BD].

3.
Mathematics is in the most general sense the science of relationships, in which one abstracts from all content of the relationships.
Relationship presumes two things, and in that case is called simple relationship, etc.
4.
The general idea of things whereby everything has only a pairwise relationship of inequality, are points on a line.
If a point can have more than a pairwise relationship, the image of it is the situation of points that are connected by lines, on a surface. But, if investigation were possible, it can concern only those points which are in a three-fold reciprocal-relationship, and where there is a relationship between the relationships.
5.
“It were extremely important, to bring the theory of differences [Gegensatz: contraries, opposites] to clarity without magnitude. Thus, for example, in the use of a plane leveller, the following differences present themselves. The position of the bubble in the glass tube at rest is determined by the geometrical axis of the tube, and a line through the plane of the feet.
In this brief fragment, we can see the complete unity in Gauss’s mind, between mathematics, metaphysics, and physics. To help grasp this, the reader should perform the following demonstration with a carpenter’s level, while thinking of the above discussion.
Hold the level on a surface so that the bubble is a rest in the middle. Now rotate the level around a line perpendicular to the surface. The bubble will not move. Now rotate the level along an axis, in the direction of the glass tube. The bubble will still not move. Now rotate one end of the level up and the other end down, on an axis parallel to the surface, but perpendicular to the level. The bubble moves. Movement of the bubble back and forth, is inseparably connected to movement of the level in a second direction. These two actions, back-forth and up-down, are not the same thing in two directions, but One two-fold action.
(If you are self-conscious, while thinking about this demonstration, you should be able to discover where the gremlins of Newtonian mysticism might be lurking in your mind.)
Acutely aware that only metaphor can adequately convey an idea, Gauss wrote to his friend Hansen on Dec. 11, 1825:
“These investigations lead deeply into many others, I would even say, into the metaphysics of the theory of space, and it is only with great difficulty that I can tear myself away from the results that spring from it, as, for example, the true metaphysics of negative and complex numbers. The true sense of the square root of [minus]1 stands before my mind [Seele] fully alive, but it becomes very difficult to put it in words; I am always only able to give a vague image that floats in the air.”
In the future, we will re-construct some of Gauss’s metaphors. We leave you today, with the following from the Epinomis:
“To the person who learns in the right way, it will be revealed that every diagram and complex system of numbers, and every structure of harmony‡ and the uniform pattern of the revolution of the stars, are a single thing applying to all these phenomena. And it will be revealed to anyone who learns correctly, as we say, fixing his eye on unity. To one who studies these subjects in this way, there will be revealed a single natural bond that links them all. But anyone who is going to pursue these studies in any other way, must ‘call on Good Fortune for help,’ as we say, too.”
—Bruce Director
|
Page Notes |
||
* Epinomis, trans. by Richard D. McKirahan, Jr., in Plato: Complete Works, ed. by John M. Cooper (Indianapolis: Hackett Publishing Company, 1997). Permission to reprint excerpts courtesy of the publisher. Bracketed comments are by the translator; Greek words and italicized comments have been supplied by Fidelio. The translator’s punctuation has been modified occassionally.
† Presented in an ongoing series of classes and pedagogical exercises by the author and collaborators.
‡ I.e, geometrical constructions, number progressions structured according to arithmetic proportions, and number progressions structured according to harmonic proportions.
|
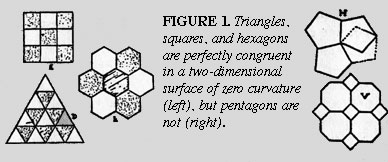
Gauss’s Concept of ‘Congruence’ In his Harmony of the World, Johannes Kepler re-defined the classical conception of congruence for modern mathematical physics, a re-definition which Carl Fredrich Gauss adopted as the basis for his ground-breaking Disquistiones Arithmeticae. Contrary to the formalist conception taught in virtually all educational systems today, “congruence” is not a mere geometrical synonym for “equality.” As Plato, nicolaus of Cusa, and Leibniz clearly understood, processes in the created world, are never susceptible to the algebraic statement of equality, because no true equality exists in the created world. Consequently, a different conception is required. In the second book of the Harmony of the World, Kepler states that “congruence” is the Latin equivalent of the Greek word “harmonia.” The geometrical representation of this concept, is illustrated by the relationship of polygons in an n-dimensional space. For example, triangles, squares, and hexagons, can be fitted together in a two-dimensional surface of zero curvature, so as to cover the entire surface; Kepler defines such figures to be perfectly congruent. Pentagons, on the other hand, cannot be fitted together in this way. [See Figure 1]
In a three-dimensional space, however, pentagons, triangles and squares are perfectly congruent, but hexagons are not. [See Figure 2]
It was a brilliant idea of Gauss, to apply Kepler’s re-statement of the classical concept of congruence, to the domain of modular arithmetic. Under Gauss’s concept of congruence, two numbers are considered congruent, if the difference between them is divisible by a third number; the two congruent numbers are called “residues,” and the third number is called a “modulus.” For example 7 ≡ 32, relative to modulus 5. Here, the relationships among all numbers, are ordered with respect to the differences (change: Gegansatz) between them. By the application of this concept of congruence, Gauss invented an entirely new domain of mathematics which he called “Higher Arithmetic.” |
|||
What is the Schiller Institute?
Carl Gauss's Fundamental Theorem of Algebra
Fidelio Table of Contents from 1992-1996
Fidelio Table of Contents from 1997-2001
Fidelio Table of Contents from 2002-present
Beautiful Front Covers of Fidelio Magazine

Join the Schiller Institute,
and help make a new, golden Renaissance!
MOST BACK ISSUES ARE STILL AVAILABLE! One hundred pages in each issue, of groundbreaking original research on philosophy, history, music, classical culture, news, translations, and reviews. Individual copies, while they last, are $5.00 each plus shipping
Subscribe to Fidelio:
Only $20 for 4 issues, $40 for 8 issues.
Overseas subscriptions: $40 for 4 issues.
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps |
Dialogue of Cultures
© Copyright Schiller Institute, Inc. 2005 All Rights Reserved.
 Fidelio, Vol. 6 ,No, 4.Winter 1997
Fidelio, Vol. 6 ,No, 4.Winter 1997