|
||
|
by Bruce Director |
||
 |
 |
|
|
Nicolaus of Cusa
|
Johannes Kepler
|
|
For related articles, scroll down or click here.
Nicholas of Cusa Moved the Earth
by Bruce Director
When a Roman soldier killed Archimedes, in 212 B.C.E. the Earth stood still. At least, that was the intention of those Mithra-cult adherents who bear ultimate responsibility for the murder.
Of course, the Earth never physically stopped. But, for approximately 1,500 years, from the death of Archimedes, until Cusa’s completion of On Learned Ignorance in A.C.E. 1440, knowledge of the Earth’s motion around the sun, with only a few notable exceptions, vanished from the Earth.
How is it that knowledge of a physical principle, whose discovery requires no more “information” than regular observations of the motions of the heavenly bodies, could be obscured for so many years? As the collapse of the so-called “New Economy” pointedly demonstrates, knowledge does not derive from information. Rather, knowledge is derived only from the cognitive power of the human mind, the power of the mind to rise above the limitations of the senses, and discern the underlying intentions (true causes), of which these sense impressions are but a reflection. The discovery of the concept of the heliocentric solar system by Archimedes’ predecessor, Aristarchus of Samos, is typical of those types of cognitive discoveries achieved through the method of Socrates and Plato. Its suppression is associated with minds stupefied by the method of Aristotle.
With the publication of On Learned Ignorance, Cusa broke the grip of Aristotle over human thought, establishing a new method for scientific investigation which revived the method of Plato, as enriched by the principles of Christianity. These principles, Cusa insisted, were comprehended through human Reason, and were therefore ecumenical, capable of being known to be true by Muslim, Jew, or other non-Christian alike.
Although a complete review of the impact of Cusa’s work for modern science would be an enormous undertaking, far beyond the scope of this present article, a significant insight into the importance of Cusa’s scientific method can be obtained by tracing the direct impact of Cusa on the astrophysics of Johannes Kepler.
The Motion of the Heavenly Bodies
Astronomy is the oldest inquiry of science. It is beyond doubt that very ancient, prehistorical cultures had developed a heliocentric conception of the solar system, as this was a necessary prerequisite for the trans-oceanic navigation practiced by Egyptian and other, earlier civilizations.
In Prometheus Bound, Aeschylus presents a metaphorical account of those early astronomical discoveries. Prometheus, who had been chained to a rock for all eternity by Zeus, in retaliation for helping humankind, speaks of his first efforts to lift man up to the level of being truly human:
Still, listen to the miseries that beset mankind—how they were witless before and I made them have sense and endowed them with reason. I will not speak to upbraid mankind but to set forth the friendly purpose that inspired my blessing.Reason tells us that Prometheus’s metaphorical account is truthful. As Lyndon H. LaRouche, Jr. has developed through his principles of physical economy, Man, the only creature endowed with cognition, must rise above his senses, and discover the principles by which the universe is composed, in order to survive and grow. Through the discovery of such universal principles, Man increases his dominion over the entire universe, from the microphysical to the astrophysical, among living processes and non-living ones; that is, the heavens and the Earth. Nowhere is this more evident, than in determining the motion of the heavenly bodies. Without such knowledge, maritime navigation, agriculture, and other advancements of human economy would be impossible. Do not make the mistake of thinking of these accomplishments in pragmatic terms, however. All practical benefits that accrue from astronomy, are a consequence of the fact, that in its pursuit, Man finds his true human nature.First of all, though they had eyes to see, they saw to no avail; they had ears, but they did not understand; but, just as shapes in dreams, throughout their length of days, without purpose they wrought all things in confusion. They had neither knowledge of houses built of bricks and turned to face the sun nor yet of work in wood; but dwelt beneath the ground like swarming ants, in sunless caves. They had no sign either of winter or of flowery spring or of fruitful summer, on which they could depend but managed everything without judgment, until I taught them to discern the risings of the stars and their settings, which are difficult to distinguish.
Yes, and numbers, too, chiefest of sciences, I invented for them, and the combining of letters, creative mother of the Muses’ arts, with which to hold all things in memory. I, too, first brought brute beasts beneath the yoke to be subject to the collar and the pack-saddle, so that they might bear in men’s stead their heaviest burdens; and to the chariot I harnessed horses and made them obedient to the rein, to be an image of wealth and luxury. It was I and no one else who invented the mariner’s flaxen-winged car that roams the sea. Wretched that I am—such are the arts I devised for mankind, yet have myself no cunning means to rid me of my present suffering.1
Anyone today can re-create, in his own mind, the same paradoxes as those known by the ancients who received Prometheus’s beneficence. Go out and look at the sky over the course of a day and night, and over the course of a year. Observe the rising and setting of the sun, the motion of the stars around the sky, the changes in position at which the sun and the stars rise, and the more complicated motions of the five planets, which the ancients called “wanderers.” Imprisoned as man is by his limited senses, all these motions are presented to him as a complicated tangle of changes in position seen as if projected onto the inside of a sphere. From the standpoint of sense perception, the Earth stands still, and all the heavenly bodies move about it in apparent circles. But, when all these motions are thought of as One, anomalies emerge, which are paradoxical with respect to pre-existing notions about the universe. It is through such paradoxes, that man discovers those concepts that reflect the true causes of the appearances. As Kepler wrote in The New Astronomy:
The testimony of the ages confirms that the motions of the planets are orbicular. It is an immediate presumption of reason, reflected in experience, that their gyrations are perfect circles. For among figures, it is circles, and among bodies, the heavens, that are considered the most perfect. However, when experience is seen to teach something different to those who pay careful attention, namely, that the planets deviate from simple circular paths, it gives rise to a powerful sense of wonder, which at length drives men to look into causes.2How Man rises above the senses to knowledge through Reason, is the implicit subject of all Plato’s dialogues. In the Timaeus, Plato presents God, the Creator of the Universe, as the Composer, who constructed the universe according to those principles of harmony which his greatest creature, Man, would recognize as beautiful. As Philo of Alexandria, the First-century A.C.E. Jewish philosopher, demonstrates, Plato’s view of God, Man, and Nature, is absolutely congruent with the Mosaic principle expressed in the beginning of the Book of Genesis, that “Man is created in the image of God.”3
The question for science, posed by Plato, is, What is the relationship of that which comes to us through the senses, and the underlying truth those sense impressions reflect? Furthermore, How does the Mind find that truth?
This requires the method Plato develops in The Republic, by which the Mind ascends successively from sense perception, to opinion, to understanding (dianoia), to reason (nous):
This then is the class that I described as intelligible, it is true, but with the reservation first that the soul is compelled to employ assumptions in the investigation of it, not proceeding to a first principle because of its inability to extricate itself from and rise above its assumptions, and second, that it uses as images or likenesses the very objects that are themselves copied and adumbrated by the class below them, and that in comparison with these latter are esteemed as clear and held in honor ... and by the other section of the intelligible I mean that which the Mind itself lays hold of by the power of dialectics, treating its assumptions not as absolute beginnings but literally as hypotheses, underpinnings, footings, and springboards so to speak, to enable it to rise to that which requires no assumption and is the starting-point of all, and after attaining to that again taking hold of the first dependencies from it, so to proceed downward to the conclusion, making no use whatever of any object of sense, but only of pure ideas moving on through ideas to ideas and ending with ideas. ...In the Timaeus, Plato shows how this method of discovery manifests itself in the physical universe. He explains that the spherical bounding of human vision conforms to, and accurately reflects, the harmonic principles embedded in the created world by God the Composer.*[L]et there be four divisions of the soul, reason answering to the highest, understanding to the second, opinion to the third, and perception of shadows to the last, and let there be a scale of them, and let us suppose that the several faculties have clearness in the same degree that their objects have truth.4
* “Wherefore he made the world in the form of a globe, round as from a lathe, having its extremes in every direction equidistant from the center, the most perfect and the most like itself of all figures; for he considered the like is infinitely fairer than the unlike.”
See footnote 5.
This is demonstrated specifically by the role of the five regular solids, both from the standpoint of geometry, and of physics [See Figure 1].
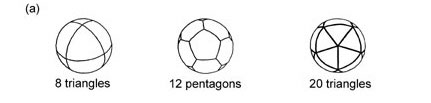
| (a) It was a discovery of Greek scientists from Pythagoras through Theatetus, that the sphere could be divided evenly in five and only five differnet ways, specifically by 4, 8, and 20 triangles; 6 squares; and 12 pentagons. Shown are the divisions into 8 and 20 equal spherical triangles, and 12 equal spherical pentagons. |
 |
|
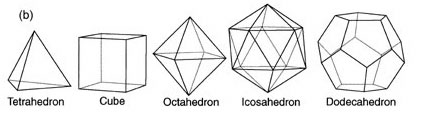
(b) When the vertices of the five possible speherical polygons are connected, they form the five regular solids, depicted below. Therse are the only solid figures composed of one and the same equilateral polygons. Plato described the Greek theory of the significance of these solids in the Timaeus, hence th name, “Platonic Solids.” |
 |
|
|||||||||||||
Plato summarizes the discoveries from Pythagoras to Theatetus, that the sphere (and, implicitly, the space it reflects) is not infinitely divisible, but rather, is restricted to five, and only five, perfectly regular divisions.†
This characteristic of the manifold of human vision, manifests itself in the physical universe, by the relationship of the five regular solids to the organization of matter. Astronomy, Plato says in The Republic, is the science of solids in motion.
Astronomy, therefore, must seek to find the harmonic principles in the complicated visible motions of the planets, as well as seek out their underlying causes. But, by underlying causes, Plato did not mean mechanical interactions of the “action-reaction” (“push-me/pull-me”) type. Rather, Plato sought the universal principles that guided the motions. Those universal principles were an expression of the intention of the Creator, who composed the world according to Reason. It is that reason which science seeks as the cause of the physical motions.
Plato recognized an inherent paradox in the study of astronomy, however. The visible motions of the planets are not the true ones:
The resolution of the this paradox depends, not upon what is in the sky, but upon what is in the mind. It depends upon the conception of Man’s nature from which it is approached.[T]hese sparks that paint the sky, since they are decorations on a visible surface, we must regard, to be sure, as the fairest and most exacting of material things; but we must recognize that they fall far short of the truth, the movements, namely, of real speed and real slowness in true number and in all true figures both in relation to one another and a vehicles of the things they carry and contain. These can be apprehended only by reaon and thought, but not by sight...
[W]e must use the blazonry of the heavens as patterns to aid in the studty of those realities, just as one would do who chanced upon diagrams drawn with special care and elaboration by Daedalus or some other craftsman or painter. For anyone acquainted with geometry who saw such designs would admit the beauty of the workmanship, but would think it absurd to examine them seriously in the expectation of finding in them the absolute truth with regard to equals ro doubles or an other ratio.5
It is in this paradox, that Plato encouraged his students to seek knowledge of the physical world. Such bold ventures produced the accomplishments of Aristarchus of Samos, who, Archimedes reports, developed a heliocentric concept of the solar system; Erathosthenes of Alexandria, who determined the sphericity of the Earth; and Archimedes, whose discoveries of principles allowed him to proclaim, “Give me a place to stand, and I will move the Earth!”
But, it is also in this paradox, that Aristotle lured the cowardly and the weak-minded away from seeking the truth, arguing that Man’s cognitive powers were ultimately impotent to raise him above his senses. For Aristotle’s physics, the laws governing the Earth were completely different than those governing the heavens. Physical action is not governed by Reason, but rather, is the result of mechanical interactions. Man, bound to the Earth, is doomed to ultimate ignorance on matters concerning the nature of God and the physical universe; he can speculate about God and physics, but, the action of his mind, according to Aristotle, is fundamentally separated from them. The only knowable truths, are those conclusions that follow deductively from a given set of axioms, according to the rules of formal logic. Such conclusions, of course, are never susceptible to determination as universal truths, as they depend upon the unprovable validity of the axioms from which they follow.
|
|||||||||||||
Aristotle’s separation of the Earth from the heavens the human mind, from God and the created world, has been used historically to justify all the unspeakable evils carried out by oligarchical regimes. According to this underlying dogma, law in Earthly society does not reflect universal principles, but, rather, as Hitler legal theorist Carl Schmitt and U.S. Supreme Court Justice Antonin Scalia assert, is the arbitrary will of whoever has the power to make the rules. This conforms perfectly to the worldview of the pro-oligarchical cults of Babylon, the Delphic Oracle of Pythian Apollo, or the Roman Mithra-cult which became transmogrified into various pseudo-Christian cults broadly characterized as Gnostic.‡
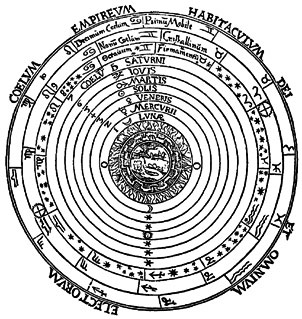
Aristotle was the standpoint adopted by Claudius Ptolemy, who rejected the accomplishments of Plato’s Academy, limiting knowledge to that which could be derived by formal logical deduction from an unchanging, fixed set of axioms, based on the sense impression that the Earth was fixed and unmoved, while the heavenly bodies moved about it in perfect circles. Ptolemy also adopted Aristotle’s mechanical explanations of the planetary motions, asserting that the heavens were filled by solid, crystalline spheres, along whose great circles the planets moved. Such motions were produced by the grinding of these solid orbs against one another, and the erratic motions of the planets were governed by a demi-god, a sort of supernatural bus driver, who steered each planet along its course.
The murder of Archimedes marked the ascendency of this craven mind-set, which gained currency under the Roman Empire as “vox populi,” what is today called “popular opinion.” A mind-set, as can be seen in the case of Archimedes, that will kill what it can’t understand, but instinctively fears.
Learned Ignorance
In On Learned Ignorance, Cusa presents a thorough-composed conception of God, Man, and Nature, and of how the human mind can, through the method of “Learned Ignorance,” rise above the senses, and come to know this conception. It would be impossible, as well as unjust and misleading, to present Cusa’s dialogue in a reduced form, and claim to have achieved an accurate representation of the ideas. Nevertheless, we attempt, imperfectly, to summarize certain facets of this concept here, for the purpose of tracing its influence on Kepler’s astrophysics.
Cusa begins: God placed a desire in all things to exist in the best manner, and he gave them the instruments by which to achieve this end. For Man, the best manner of existence is to know the truth, for which he has been endowed with the powers of cognition. “The intellect insatiably desires to attain unto the true through scrutinizing all things by means of its innate faculty of inference.” The mind judges that which it does not know, by making a comparative relationship with what it does.
However, this presents an inherent paradox for science:
Both the precise combinations in corporeal things and the congruent relating of known to unknown surpass human reason to such an extent that Socrates seemed to himself to know nothing except that he did not know. ... Therefore, if the foregoing points are true, then since the desire in us is not in vain, assuredly we desire to know that we do not know. If we can fully attain unto this knowledge or our ignorance, we will attain unto learned ignorance. ... The more he knows that he is unknowing, the more learned he will be.6So, it is in the nature of knowing the way we do not know, that we are able to gain increasingly less-imperfect knowledge of the truth.
Cusa begins by investigating through Learned Ignorance, the nature of the Absolute Maximum, “which the faith of all nations indubitably believes to be God.” This Absolute Maximum, while pure Oneness, is by its very nature triune, comprising oneness, equality, and union.
|
|||||||||||||
Ironically, one of Cusa’s most important discoveries concerning the principle of Learned Ignorance, was his correction of a conceptual error of Archimedes, specifically the impossibility of squaring the circle.*
This discovery provided a means to grasp more clearly the relationship of God to Man, and the created world, and also laid the basis for understanding the existence and significance of transcendental magnitudes. Both concepts were crucial to Kepler’s later discoveries. Cusa writes,
Whatever is not truth, cannot measure truth precisely. (By comparison, a noncircle cannot measure a circle, whose being is something indivisible.) Hence, the intellect, which is not truth, never comprehends truth so precisely that truth cannot be comprehended infinitely more precisely. For the intellect is to truth as an inscribed polygon is to the inscribing circle. The more angles the inscribed polygon has, the more similar it is to the circle. However, even if the number of its angles is increased ad infinitum, the polygon never becomes equal to the circle unless it is resolved into an identity with the circle.This incommensurability of the curved to the straight, provides the means by which to grasp the relationship between God, the Creator, and the created world; The Absolute Maximum bounds the universe in the same way that the circle bounds the polygon. Just as the polygon is derived from the circle, not the circle from the polygon, so the Absolute Maximum unfolds and enfolds the Universe, which is an imperfect likeness of it. The triune nature of the Absolute Maximum is thus expressed in the Universe, as the relationship between the Creator, the Created, and the act of creation.
But, since the universe is a “contracted maximum,” those principles are reflected imperfectly. From this standpoint, Cusa draws specific conclusions concerning the nature of the physical universe:
Wherefore it follows, that, except for God, all positable things differ. Therefore, one motion cannot be equal to another; nor can one motion be the measure of another, since, necessarily, the measure, and the thing measured differ. Although these points will be of use to you regarding an infinite number of things, nevertheless, if you transfer them to astronomy, you will recognize that the art of calculating lacks precision, since it presupposes that the motion of all the other planets can be measured by reference to the motion of the sun. Even the ordering of the heavens, with respect to whatever kind of place, or with respect to the risings and settings of the constellations, or to the elevation of a pole, and to things having to do with these, is not precisely knowable. And since no two places agree precisely in time and setting, it is evident that judgments about the stars are, in their specificity, far from precise.From these principles, Cusa rejects the fraud of Claudius Ptolemy’s geocentric solar system:
Hence, if we consider the various movements of the spheres, we will see that it is not possible for the world-machine to have as a fixed and immovable center, either our perceptible earth or air or fire or any other thing. For, with regard to motion, we do not come to an unqualifiedly minimum, i.e., a fixed center. Hence the world does not have a fixed circumference. ... Therefore, since it is not possible for the world to be enclosed between a physical center and a physical circumference, the world of which God is the center and the circumference is not understood. ...The concluding statement in the extract above, was a declaration that the Emperor—Aristotle—had no clothes. Cusa was stating what anyone could see in the heavens for himself, that the physical universe did not obey the a priori assumptions of Aristotle’s world of a fixed center. The stars themselves compelled the discovery of a new concept concerning Man and Nature. More importantly, Cusa was demonstrating the method by which the human mind could attain truthful knowledge of the motions of the heavenly bodies.Therefore, the earth which cannot be the center, cannot be devoid of all motion. Instead, it is even necessary that the earth be moved. ...
And since we can discern motion only in relation to something fixed, viz., either poles or centers, and since we presuppose these poles or centers when we measure motions, we find that as we go about conjecturing, we err with regard to all measurements. And we are surprised when we do not find that the stars are in the right position according to the rules of measurement of the ancients.
Kepler’s Transformation of Astrophysics
Cusa’s revolution began to force a retreat of the Aristotelian control over astronomy. Confronted with the discrepancy between the true motions of the planets, and the motions predicted by the geocentric system of Claudius Ptolemy, Nicholas Copernicus re-introduced the heliocentric conception of the solar system of Aristarchus of Samos. However, the poison of Aristotle was still embedded in the Copernican system. While he copied the form of Cusa’s conclusions, placing the Earth in motion around the sun, Copernicus failed to apply Cusa’s method of Learned Ignorance. Under the Copernican system, the planets all revolve around the sun in perfect circles—that is, the non-uniform motion of the planets had ultimately to be resolved mathematically into uniform circular action—despite the fact that Cusa had already shown that no such perfect motion was possible in the created world. Even more fundamentally, Copernicus would not totally break with the Aristotelian stricture that knowledge of the physical universe, and the principles by which God composed it, were essentially beyond human comprehension. Thus, Copernicus never claimed the heliocentric system was actually true, but only that it provided a better means of mathematical computation.
In 1595, Johannes Kepler brought forth his first work on planetary motion, Mysterium Cosmographicum (The Secret of the Universe), in which Cusa’s method of Learned Ignorance was applied to achieve a revolutionary conception of the nature of the physical universe.
As the subtitle of this work indicates, Kepler completely rejected Aristotle and, instead of simply providing just another mathematical model, sought “the true and particular causes of the number, size, and periodic motions of the heavens.” By true causes, Kepler understood, as did Plato and Cusa, the Reason, or intention, according to which God composed the universe as he did. As Kepler announced at the beginning of the Mysterium:
I pass over in silence the fact that this very matter, of Creation, which the philosophers [Aristotelians-BD] denied, is a strong argument, when we perceive how God, like one of our own architects, approached the task of construction the universe with order and pattern, and laid out the individuals parts accordingly as if it were not art which imitated Nature, but God himself had looked to the mode of building of Man who was to be.7These words of Kepler echo those of Cusa from the On Learned Ignorance of nearly 150 years earlier:
Who would not admire this Artisan, who with regard to the spheres, the stars, and the regions of the stars, used such skill that there is though without complete precision both harmony of all things and a diversity of all things? This Artisan considered in advance the sizes, the placing, and the motion of the stars in the one world; and He ordained the distances of the stars in such way that unless each region were as it is, it could neither exist nor exist in such a place and with such an order nor could the universe exist.Kepler found that the ordering principle determining the number of the planets, their sizes, and the positions of their orbits, was expressed by the proportions of the five perfectly regular solids presented by Plato in the Timeaus. Just as important as this result, was the method by which Kepler arrived at it, since it exemplified Cusa’s method.
As previously stated, it is already a significant advance to seek the true causes of the motions of the heavenly bodies. But, it was a further revolution to actually determine, “Why it was that way and not otherwise,” as Kepler stated in the beginning of the Mysterium. To discover this, Kepler first attempted to find some series of numbers, which would correspond to the actual number of planets and the size of their orbits. Despite much effort, this proved fruitless. Failing at that, Kepler sought the principle in two dimensions, seeking a series of inscribed and circumscribed polygons, whose proportions would correspond to the number and size of the actual planetary orbits. This too proved fruitless. Finally Kepler made the leap, “Why should there be plane figures between solid spheres? It would be more appropriate to try solid bodies.” Thus was born Kepler’s discovery that the number, size, and position of the (then-)visible planets, corresponded to the principle of construction of the five Platonic solids [See Figure 2].
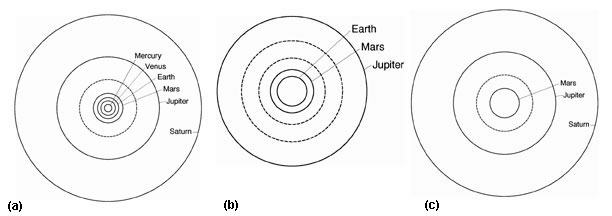 |
|
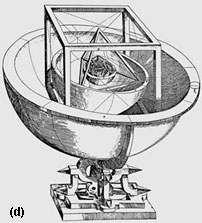 |
The ordering of the number of the sizes of the orbits of the six plantets visible to the naked eye, does not conform to any sequence of numbers or plane polygons. (a) The relative sizes of the planetary orbits, shown heuristically.(b) If the distance between the orbits of Earth and Mars is extrapolated outward, two orbits should occur between Mars and Jupiter (dashed orbits). (c) If the distance between theorbits of Saturn and Jupiter is extrapolated inward, one orbit should occur, where, in fact, no planets visible to the naked eye exist. Kepler discovered that the ordering of the visible planets cooesponded to the ordering achieved by inscribing and circumscibing spheres around the five Plantonic solids, in the order debicted in illustration (d) from the “Mysterium Comographicum.” Kepler later showed that the anomaly betwwn Mars and Jupiter corresponded to a dissonance in the harmonic relationships bewteen the orbits. In 1801, Carl Fl Gauss confirmed Kepler’s hypothesis, when he demonstrated that the orbits in this region were “unstable,” and it was populated with planetary fragments, which today are called asteroids [dashed orbit in (a)]. [See Jonhathan Tennenbaum and Bruce Director, “How Gauss Determined the Orbit of Ceres” Fidelio Summer 1998 (PDF only) |
In the Mysterium, Kepler attributes this discovery directly to Cusa’s method:
It was matter which God created in the beginning; and if we know the definition of matter, I think it will be fairly clear why God created matter and not any other thing in the beginning. I say that what God intended was quantity. To achieve it he needed everything which pertains to the essence of matter; and quantity is a form of matter, in virtue of its being matter, and the source of its definition. Now God decided that quantity should exist before all other things so that there should be a means of comparing a curved with a straight line. For in this one respect Nicholas of Cusa and others seem to me divine, that they attached so much importance to the relationship between a straight and a curved line and dared to liken a curve to God, a straight line to his creatures; and those who tried to compare the Creator to his creatures, God to Man, and divine judgements to human judgements did not perform much more valuable a service than those who tried to compare a curve with a straight line, a circle with a square.The significance of Cusa’s demonstration of the transcendental relationship between the curved and the straight, was thus demonstrated by Kepler to manifest itself in the actual construction of the physical universe. Kepler’s further discoveries demonstrated that this manifestation was not simply limited to the role of the Platonic solids in the construction of the heavens, but, as Cusa himself understood, was embedded in the very nature of the physical action.And although under the power of God this alone would have been enough to constitute the appropriateness of quantities, and the nobility of a curve, yet to this was also added something else which is far greater; the image of God the Three in One in a spherical surface, that is of the Father in the center, the Son in the surface, and the Spirit in the regularity of the relationship between the point and the circumference. For what Nicholas of Cusa attributes to the circle, others as it happens have attributed to the globe; but I reserve it solely for a spherical surface.
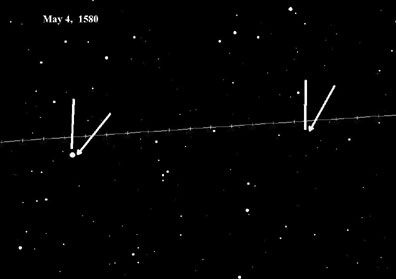
Kepler’s 1609 The New Astronomy is based on this deeper manifestation of the transcendental relationship between the curved and the straight. Kepler’s polyhedral hypothesis, that the number and size of the planetary orbits were determined by inscribing and circumscribing spheres around the five Platonic solids, was not sufficient to account fully for the true motions of the planets. Orbits derived from this hypothesis, were circles. The true motions of the planets indicated the existence of another principle—namely, that the planets do not move uniformly in their orbits. They can be observed to be always speeding up to a maximum speed and slowing down to a minimum [See Figure 3].
|
 (a) (a) |
|
 (c) |
 (b) (b) |
Ptolemy, Copernicus, and Kepler’s sometime collaborator, Tycho Brahe, all calculated this observed non-uniform motion as a result of colligating circles [See Figure 4].
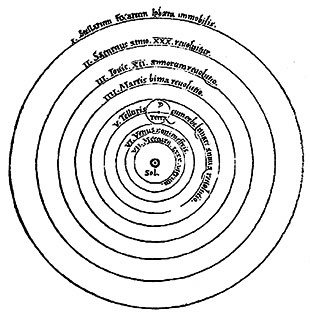
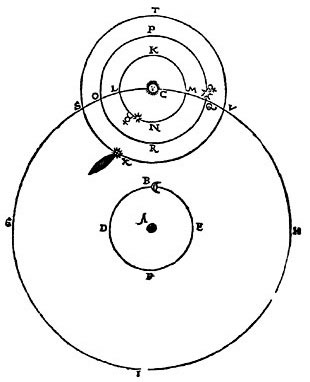
 (a) Ptolemaic system: Earth-centered (a) Ptolemaic system: Earth-centered |
(a) The Ptolemaic system, with the Earth at the center and all the planets and the sun moving around it in perfect circles. (b) The copernican system, with the sun at the center, and all the planets, including the Earth, moving around in perfect circles. (c)The system of Tycho Brahe, in wich the Earth is at the center, and all the planets move about the sun in Perfect circles, while the sun moves about the Earth in a perfect circle.
In “The New Astronomy,” Kepler demonstrated that all three systems gave exactly the smae computational results, so there was no way to tell which one was tgrue. Despite the fact that all three were readcally different, there was a common error that pervatded them. All three were mathematical models for the purpose of predicting the motions of the planets, while making nmo attempt to discover the physical causes. Consequently, all three imposed the mathematics of perfect circles and juniform motion onto the planetary orbits, when the physical observations showed otherwise. |
(b) Copernican system: sun-centered |
 (c) System of Tycho Brahe: mixed Earth- and sun-centered. |
Here, Kepler pointed out that the three radically different systems shared a common error, the embedded error of the Aristotle. All three imposed, a priori, the mathematics of perfect circles—and hence, assumed the reality of uniform motion—on the physical universe: “The three opinions are for all practical purposes equivalent to a hair’s breadth, and produce the same results,” he wrote, in the introduction to The New Astronomy.
Consequently, it is impossible to tell which of the three opinions is true, says Kepler. The common error in all three opinions is, that they assume a pre-existing mathematical structure (perfect circles), and then force the physical observations to conform to that mathematical idea. As Copernicus puts it in his Revolutions of the Heavenly Spheres: “The movement of the celestial bodies is regular, circular, and everlasting—or else compounded of circular movements.” But, the observed motions of the planets are not regular, so why assume a priori that these motions must derive from circles?
Kepler took a completely different, revolutionary approach, one based on Plato and Cusa. Rather than force the observations to conform to pre-existing mathematical assumptions, he sought the physical reason for the observed non-uniform motion, and then conformed his mathematics to that physical hypothesis:
Indeed, all things are so interconnected, involved, and intertwined with one another that after trying many different approaches to the reform of astronomical calculations, some well trodden by the ancients and others constructed in emulation of them and by their example, none other could succeed than the one founded upon the motions physical causes themselves, which I establish in this work.What was so frightening about the planets having non-uniform motion, that it kept Aristotle’s grip over three very different types of thinkers, such as Ptolemy, Brahe, and Copernicus? Again, Cusa gives the answer.
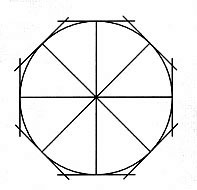
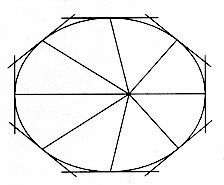
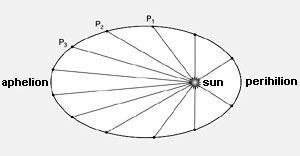
If the planets were moving uniformly about the sun in perfect circles, then each planet’s motion would be governed by an unchanging principle; that is, its speed would be constant, it would always be the same distance from the sun (or Earth), and its direction would always be at a right angle to a line connecting the planet to the sun [See Figure 5(a)]. However, if the planets were moving non-uniformly, the speed and direction would be constantly changing [See Figure 5(b)].
| (a) Uniform circular action. The direction of the planet, represented by the tangents to the circle, is always perpendicular to the lines connnecting it to the center of the orbit. A mind trying to maintain a circular orbit, would thus have only to keep its speed and direction constant, in order to maintain this orbit. Once it started along this path, it could maintain it without any change (decisions). (b) Non-uniform elliptical action. Here the direction of the planet, shown by the angle formed by the tangent and the line connection it to the focus of the orbit, is always changing, as is its speed. A mind trying to maintain this orbit would have to make a desision at each moment, how much to speed up or slow down, and how much to alter its direction. The existence of such action implies the existence of a principle congruent with cognition in the physical universe. |
|
|
(a)
|
(b)
|
Kepler demonstrates that the relationship of the speed and direction of the planet at each moment, to the characteristic of the whole orbit, depends on those transcendental magnitudes discovered by Cusa.
This implies that a quality of cognition, or Mind, is governing the planet’s motion. But, how does the planet know how to adjust its speed and direction at each moment? And, more significantly, and more terrifying to an Aristotelian, “How can the human mind know what the planet knows?” Especially, since the planet’s action depends upon just those transcendental magnitudes, which Cusa had demonstrated were not susceptible to precise mathematical calculation?
This problem is not so terrifying for a thinker who follows Cusa’s principle of Learned Ignorance. As cited above, Cusa had already stated that physical action could not occur according to perfect circles, and that precise calculation of a planet’s motion is as impossible as squaring the circle. Rather than cringe at the expression of transcendental magnitudes, Cusa’s Learned Ignorance teaches us to rejoice at this paradox, as it urges us on to new discoveries. But, the question remains, What is the underlying principle that expresses itself as the quality of Mind, governing the planet’s orbit?
That quality of Mind, is not, as Aristotelians such as Ptolemy maintain, an irrational demi-god residing in each planet, possessed with innate intelligence, and capable of arbitrary action. Rather, each planet acts as if it had a Mind, because its action expresses an intention of the underlying principles governing the universe as a whole. That is, the planet’s motion expresses the intention of the Divine Mind, whose intentions also govern the human mind, created in the image of God.
This Keplerian concept of Mind is congruent with the thinking of Plato and Cusa. For example, in On Learned Ignorance, Cusa revives Plato’s concept of Mind, resituating it from the standpoint of Christianity, and cleaning up the influence of Aristotle on the medieval Neo-Platonists, who, in Cusa’s time, were the dominant exponents of Platonism:
All wise agree that possible being cannot come to be actual except through actual being, for nothing can bring itself into actual being, lest it be the cause of itself, for it would be before it was. ... Some called this excellent actualizing nature “mind”; others called it “intelligence,” others “world-soul,” others, “fate-substantiated,” others (e.g., Platonists) “connecting necessity. ...However, the following view was acceptable to the Platonists: that such distinct plurality of exemplars in the connecting necessity is in a natural order from one infinite Essence, in which all things are one. Nevertheless, they did not believe that the exemplars were created by this one infinite Essence, but that they descended from it in such way that the statement, “God exists,” is never true without the statement “The world exists,” also being true. And they affirmed that the world-soul is the unfolding of the Divine Mind, so that all things which in God are one Exemplar are, in the world-soul, many distinct exemplars. ...
Many Christians consented to this Platonistic approach. Especially since the essence of stone is distinct from the essence of man and in God there is neither differentiation nor otherness, they thought it necessary that these distinct essences (in accordance with which, things are distinct) be subsequent to God but prior to things (for the essence precedes the thing): and they thought this too with regard to intelligence, the mistress of the orbits. ...
The Platonists spoke quite keenly and sensibly, being reproached, unreasonably, perhaps, by Aristotle, who endeavored to refute them with a covering of words rather than with deep discernment. But through learned ignorance I shall ascertain what the truer view is. ...
Therefore, it is necessary to understand clearly the following matters; since a Platonic type world-soul must be regarded as a certain universal form which enfolds in itself all forms but which has actual existence only contractedly in things and which in each thing is the contracted form of this thing, as was said earlier regarding the universe: then not such a world-soul but God who is one Word creates all things, regardless of how different from one another they are is efficient, the formal and the final Cause of all things; and there can be no created thing which is not diminished from contraction and does not fall infinitely short of the divine work. God alone is absolute: all other things are contracted. Nor is there a medium between the Absolute and the contracted as those imagined who thought that the world-soul is mind existing subsequently to God but prior to the world’s contraction. For only God is “world-soul”: and “world-mind” in a manner whereby “soul” is regarded as something absolute in which all the forms of things exist actually. Indeed, the philosophers were not adequately instructed regarding the Divine Word and Absolute Maximum. And so, they envisioned mind and soul and necessity as present uncontractedly in a certain unfolding of Absolute Necessity.
The Harmonies: A Still More Basic Principle
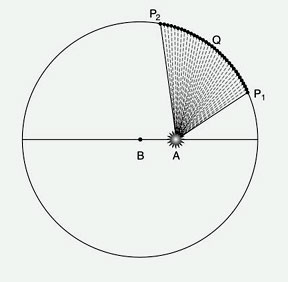
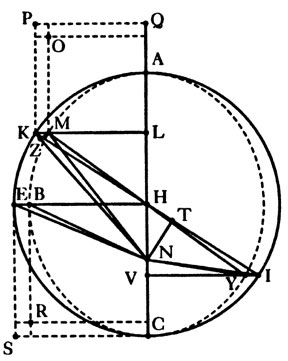
From these considerations, Kepler came to the discovery that the non-uniform motion of the planets was not simply an appearance, but was the true physical motion. This led him to the ultimate discovery, that the principle governing this non-uniform motion was expressed in the principle, “equal areas, equal times,” and that the orbits of the planets were, in first approximation, elliptical [See Figure 6].
|
(a)
|
(b)
|
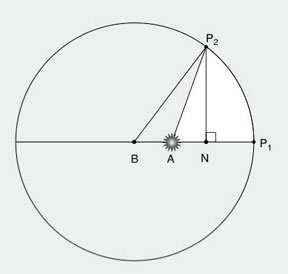
| Kepler’s revolution was, to derive the principles of planetary motion from physical principles, not mathematical ones. He conceived that the sun moved all the prlanets by a virtue (power) emanating from it, whose intensity diminished with distance. This, if the planet were moving in an orbit in which its distance from the sun varied, it would physically speed up and slow down as it moved around the sun (a) The planet at P1 is closer to the sun A, than at P2. Thus, as the planet moves from P1 to P2, ti is always slowing down. This means that equal portions of the planet”s period do not correspond to equal distances along its orbital path. Kepler showed that these equal portions corresponded to equal areas swept out by a line connecting the planet to the sun (b) Kepler measured these areas. The area swept out as the planet moves from P1 to P2 is the white area (P1-P2-A). That area is measured by the protion of the circle, P1-BN-P2 minus the traingle P2-B-A. The area of theat triangel is the distance BA times the height P2-N. But, the line P2-N, as Cusa showed, is inommensurable with the arc P1-P2. This, the principle of non-uniform planetary motion is dependent on the magnitudes which are not susceptible of precise calculation. This gave rise to the famous “Kepler problem”: If Kepler know where the planet had been, he could calculate what portion of the orbit (time) had elapsed. But, owing to the transcendental relationship between the line and curve, he could not precisely calculate where the planet would be when an equal amount of time would have elapsed, Kepler called on future geometers to solve this problem, which provoked Leibniz to develop the calculus. Kepler’s initial discovery of the “equal areas, equal times” principle was developed under the assumption that the orbit was circular, with the sun at an eccentric point. After comparing his results to the true observations, Kepler found he was 8′ of arc off. It is a tribute to Kepler’s genius, that he saw that this small discrepancy was a matter of principle, not simply a minor error. He subsequently revised all his work, and discovered that the planetary orbits were ellipses, as depicted, in (c). (d) Kepler’s diagram from “The New Astronomy,” The dotted curve is an ellipse. As you can see, this ellipse is very close to a circle, but as Cusa had forecast in “On Learned Ignorance,” these is no perfectly circular motion in the created world. |
(c)
|
| (d)
|
But this left open the question, What were the principles governing the determination of the eccentricities?, since Kepler’s polyhedral hypothesis accounts only for circular orbits.
Pursuing Cusa’s method further, Kepler sought “a still more basic principle,” which would answer the question, Why these eccentricities and not others?
To answer this question, Kepler looked to the relationship between the maximum and minimum speeds of the planets, and found this relationship to correspond to musical harmonies [See Figure 7].
 |
|
| After discovering that the planetary orbits were eccentric, Kepler sought to discover a “more basic principle” that would account for the reason for the particular eccentricies they exhibited. He measured each planet”s maximum speed when it was closest to the sun (perihelion), and the minimum speed when the planet was farthest from the sun (aphelion), as if he were observing the planet”s motion from the sun itself. Then, comparing the speeds of neighboring planets, he found that the ratios of these intervals corresponded to those intervals which human beings considered harmonic in musical compostiions. Shown are a chart of the ratios at perihelion and aphelion (above), and their representations as musical intervals (right), taken from The New Astronomy. |  |
As he stated in the introduction to Book IV of The Epitome of Copernican Astronomy:
In the farthest movements of any two planets, the universe was stamped with the adornment of harmonic proportions, and accordingly, in order that this adornment might be brought into concord with the movements, the eccentricities which fell to the lot of each planet had to be brought into concord.8Kepler’s harmonic orderings, once again, revealed a new manifestation of concepts originally brought forward by Cusa. The harmonic intervals, which Kepler found to be reflected among the planetary orbits, were, like the individual motions of the planets, dependent on transcendental magnitudes, a result anticipated by Cusa in On Learned Ignorance:
Press onward: Conformably to the rule, there is no precision in music. Therefore it is not the case that one thing perfectly harmonizes with another in weight or length or thickness. Nor is it possible to find between the different sounds of flutes, bells, human voices, and other instruments comparative relations which are precisely harmonic so precisely that a more precise one could not be exhibited. ... Ascend now to the the recognition that the maximum, most precise harmony is an equality-of-comparative relation which a living and bodily man cannot hear. For since this harmony is every proportion (ratio), it would attract to itself our soul’s reason [ratio] just as infinite Light attracts all light so that the soul, freed from perceptible objects, would not without rapture hear with the intellect’s ear this supremely concordant harmony. A certain immensely pleasant contemplation could here be engaged in not only regarding the immortality of our intellectual, rational spirit (which harbors in its nature incorruptible reason, through which the mind attains, of itself , to the concordant and the discordant likeness in musical things), but also regarding the eternal joy into which the blessed are conducted, once they are freed from the things of this world. But I will deal with this topic elsewhere.These musical paradoxes, sparked by Cusa and Kepler, laid the groundwork for their more complete elaboration, in the domain of musical composition, by J.S. Bach’s development of the well-tempered system of polyphony.
Kepler developed his completed hypothesis of planetary motion in his 1619 Harmonies of the World. At the conclusion of that work, Kepler appended an, “Epilogue Concerning the sun by Way of Conjecture,” which provides a poetical summary of the development of his ideas from Pythagoras through Cusa:
From the celestial music to the hearer; from the Muses to Apollo the leader of the Dance; from the six planets revolving and making consonances, to the sun at the center of all the circuits, immovable in place, but rotating into itself. ...And so, it is fitting that anyone wishing to study astronomy today, should begin by first getting to know Nicolaus of Cusa, whose birth we celebrate this year.[N]ot only does light go out from the sun into the whole world, as from the focus or eye of the world, as life and heat from the heart, as every movement from the King and mover, but conversely also by royal law these returns, so to speak, of every lovely harmony are collected in the sun from every province in the world, nay, the forms of movements by twos flow together and are bound into one harmony by the work of some mind ... .
By that commencement, at the same time, he [Proclus] indicates what the Pythagoreans understood by the word of fire ... and at the same time he transfers his whole hymn from the body of the sun and its quality and light, which are sensibles, to the intelligibles, and he has assigned to that intellectual fire of his—perhaps the artisan fire of the Stoics—to that created God of Plato, that chief or self-ruling mind, a royal throne in the solar body, confounding into one the creature and Him through Whom all things have been created. But we Christians, who have been taught to make better distinctions, know that this eternal and uncreated “Word,” Which was “with God” and Which is contained by no abode, although He is within all things, excluded by none ... .
[A]s for the remainder concerning that abode, we believe it superfluous to inquire into it too curiously or to forbid the senses or natural reasons to investigate that which the eye has not seen nor the ear heard and into which the heart of man has not ascended; but we duly subordinate the created mind—of whatsoever excellence it may be—to its Creator, and we introduce neither God-intelligences with Aristotle and the pagan philosophers nor armies of innumerable planetary spirits with Magi, nor do we propose that they are either to be adored or summoned to intercourse with us by theurgic superstitions, for we have a careful fear of that; ... .
But if it is permissible, using the thread of analogy as a guide, to traverse the labyrinths of the mysteries of nature, not ineptly, I think, will someone have argued as follows: The relation of the six spheres to their common center; thereby the center of the whole world, is also the same as that of unfolded Mind (dianoia) to Mind (nous), according as these faculties are distinguished by Aristotle, Plato, Proclus, and the rest; and the relation of the single planets’ revolutions in place around the sun to the unvarying rotation of the sun in the central space of the whole system ... is the same as the relation of unfolded Mind to Mind, that of the manifold discourses of ratiocination to the most simple intellection of the mind. For as the sun rotating into itself moves all the planets by means of the form emitted from itself, so too—as the philosophers teach—Mind, by understanding itself and in itself all things, stirs up ratiocinations, and by dispersing and unrolling its simplicity into them, makes everything understood. And the movements of the planets around the sun at their center and the discourses of ratiocinations are so interwoven and bound together that, unless the Earth, our domicile, measured out the annual circle, midway between the other spheres—changing from place to place, from station to station—never would human ratiocination have worked its way to the true intervals of the planets and to the other things dependent from them, never would it have constituted astronomy.9
|
Footnotes |
||
1. Aeschylus, Prometheus Bound, ed. by Herbert Weir Smyth, www.perseus.tufts.edu.
2. Johannes Kepler, The New Astronomy (Astronomia Nova), trans. by William Donahue (Cambridge: Cambridge University Press, 1992).
3. See Philo, “On the Account of the World’s Creation Given by Moses,” trans. by F.H. Colson and G.H. Whitaker, in Philo, I, Loeb Classical Library (Cambridge, Harvard University Press, 1929.)
4. Plato, The Republic, trans. by Paul Shorey, in Plato, VI (Books VI-X), Loeb Classical Library (Cambridge, Mass.: Harvard University Press, 1935).
5. Plato, Timaeus, trans. by R.G. Bury, in Plato, IX, Loeb Classical Library (Cambridge, Mass.: Harvard University Press, 1929). (back to box)
6. Nicholas of Cusa on Learned Ignorance: A Translation and Appraisal of De Docta Ignorantia, trans. by Jasper Hopkins (Minneapolis: The Arthur Banning Press, 1985), 2nd edition.
7. Johannes Kepler, Mysterium Cosmographicum (The Secret of the Universe), trans. by A.M. Duncan (New York: Abaris Books, 1981).
8. Johannes Kepler, Epitome of Copernican Astronomy: Books IV and V, trans. by Charles Glenn Wallis, in Great Books of the Western World (Chicago: Encyclopedia Britiannica, 1939).
9. Johannes Kepler, The Harmonies of the World (Harmonice Mundi) trans. by Charles Glenn Wallis, ibid.
![]()
schiller@schillerinstitute.org
The Schiller Institute
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Thank you for supporting the Schiller Institute. Your membership and contributions enable us to publish FIDELIO Magazine, and to sponsor concerts, conferences, and other activities which represent critical interventions into the policy making and cultural life of the nation and the world.
Contributions and memberships are not tax-deductible.
VISIT THESE OTHER PAGES:
Home | Search | About | Fidelio | Economy | Strategy | The LaRouche Frameup | Conferences
Links | LaRouche | Music | Join | Books | Concerts | Highlights | Education |
Health | Spanish Pages | Poetry | Dialogue of Cultures
Maps | What's New
© Copyright Schiller Institute, Inc. 2006. All Rights Reserved.
![]()
schiller@schillerinstitute.org
The Schiller Institute
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Thank you for supporting the Schiller Institute. Your membership and contributions enable us to publish FIDELIO Magazine, and to sponsor concerts, conferences, and other activities which represent critical interventions into the policy making and cultural life of the nation and the world.
Contributions and memberships are not tax-deductible.
VISIT THESE OTHER PAGES:
Home | Search | About | Fidelio | Economy | Strategy | The LaRouche Frameup | Conferences
Links | LaRouche | Music | Join | Books | Concerts | Highlights | Education |
Health | Spanish Pages | Poetry | Dialogue of Cultures
Maps | What's New
© Copyright Schiller Institute, Inc. 2006. All Rights Reserved.