| A SYMPOSIUM ON THE 600TH ANNIVERSARY OF THE BIRTH OF CARDINAL NICOLAUS OF CUSA |
|
|
Nicolaus of Cusa’s ‘On the Quadrature of the Circle’
by William F. Wertz, Jr. |
 Nicoluas of Cusa |
Nicolaus of Cusa’s ‘On the Quadrature of the Circle’
by William F. Wertz, Jr.
Lyndon LaRouche has emphasized that, if humanity is to escape a descent into a new Dark Age, and accomplish the unprecedented task of proceeding directly from a global financial collapse into a new Golden Renaissance, it will be because we have become self-consciously creative by mastering the creative breakthroughs of our predecessors. The purpose of this article is to help you, the reader, to replicate in your own mind the fundamental scientific discovery made by Nicolaus of Cusa in his “On the Quadrature [Squaring] of the Circle” (1450).
As LaRouche has written in many locations, but especially in Appendix A to “The Truth About Temporal Eternity,” in working through Archimedes’ (287-212 B.C.E. ) propositions regarding the “Measurement of a Circle,” Nicolaus of Cusa made a discovery which launched modern physical science. So important was this discovery and the method employed by Cusanus in making it, that it can truly be said, that they are responsible for mankind’s having achieved a greater increase in its potential relative population density from the Council of Florence (1439-40) to today, than in all of prior human history.
The first indication of Cusa’s work on the quadrature of the circle comes in On Learned Ignorance, written in 1439-40, immediately after the Council of Florence. There are three references in this piece to the quadrature of the circle. In Book I, Chapter III, entitled the “Precise Truth Is Incomprehensible,” Cusanus writes:
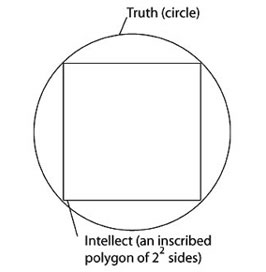
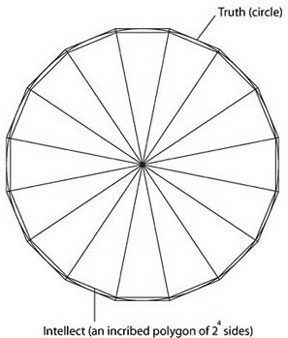
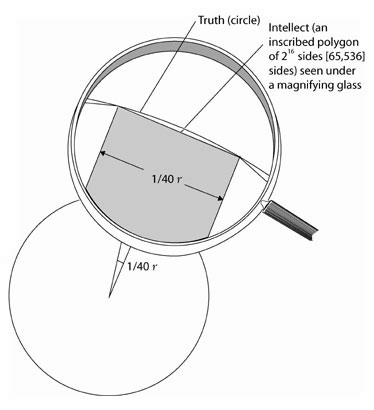
Whatever is not truth cannot measure truth precisely. (By comparison, a non-circle cannot measure a circle, whose being is something indivisible.) Hence, the intellect, which is not truth, never comprehends truth so precisely that truth cannot be comprehended infinitely more precisely. For the intellect is to truth as [an inscribed] polygon is to [the inscribing] circle. The more angles the inscribed polygon has, the more similar it is to the circle. However, even if the number of its angles is increased ad infinitum, the polygon never becomes equal [to the circle], unless it is resolved into an identity with the circle. [See Figure 1]
|
“The intellect is to truch as an incribed polygon is to the inscribing circle. The more angels the inscribed polygon has, themore similar is is to the circle.”
 |
“However, even if the number of its angles is increased ad infiniutm, the polygon never becomes equal to the circle.”
 |
 |
|
In this passage, Cusanus makes the point that the circle is indivisible by nature compared to the non-circle, i.e., the polygon, the rectilinear sides of which can always be multiplied without changing its intrinsic nature. In this location, Cusanus uses the qualitative difference in the nature of a circle and a polygon, to underscore the fact that even though the human mind is created in the image of God, because it is created, i.e., finite, it cannot precisely attain the Truth itself, which is infinite. As Cusanus further writes in the same location, “there is no comparative relation of the infinite to the finite.”
In Book III, Chapter I, Cusanus writes:
Hence, there is nothing in the universe which does not enjoy a certain singularity that cannot be found in any other thing, so that no thing excels all others in all respects or [excels] different things in equal measure. By comparison, there can never in any respect be something equal to another; even if at one time one thing is less than another and at another [time] is greater than this other, it makes this transition with a certain singularity, so that it never attains precise equality [with the other]. Similarly, a square inscribed in a circle passes—with respect to its size—from being a square which is smaller than the circle to being a square larger than the circle, without ever arriving at its equal. And an angle of incidence increases from being lesser than a right [angle], to being greater [than a right angle], without the medium of equality.Finally, in Book III, Chapter IV, Cusanus writes in respect to Jesus Christ, who is God and man:
But the maximum intellect, since it is the limit of the potentiality of every intellectual nature and exists in complete actuality, cannot at all exist without being intellect in such way that it is also God, who is all in all. By way of illustration: Assume that a polygon inscribed in a circle were the human nature, and the circle were the divine nature. Then, if the polygon were to be a maximum polygon, than which there cannot be a greater polygon, it would exist not through itself with finite angles, but in the circular shape. Thus, it would not have its own shape for existing—[i.e., it would not have a shape which was] even conceivably separable from the circular and eternal shape.Thus, Jesus Christ, who is one person, but has two natures, divine and human, is the exception to what Cusanus writes in Book I, Chapter III about the impossibility of the polygon ever becoming equal to the circle. In the case of Jesus Christ, the two natures are actually resolved in the one person.
Although Cusanus does not explicitly reference St. Anselm’s proof of the existence of God in this location, nonetheless there is a definite connection. In his Proslogium, Anselm had argued that a being exists “than which a greater cannot be conceived.” What Cusanus argues in the case of Jesus Christ is, that the maximum polygon, than which there cannot be a greater polygon, is an infinite polygon, and thus simultaneously an infinite circle.
As can be seen from the above, Nicolaus of Cusa’s treatment of the quadrature of the circle derives from his concern with theological matters. I would even maintain that the scientific advance that he made over and against Archimedes, derives from his preoccupation with the central issue of the Council of Florence, the issue of the Filioque—the idea that the Holy Spirit proceeds from the Father and the Son. On Learned Ignorance was written immediately after the Council of Florence, and thus reflects Cusanus’s intellectual concentration on this issue.
In Christian theology, the Son, as the second person in the Trinity, is equal to the Father. It is the notion of absolute equality appropriate to the Trinity, as opposed to the equality defined as approximation, which is the basis for Cusanus’s advance over Archimedes. In “On the Quadrature of the Circle,” Cusanus makes this distinction between the notion of equality as approximation, which Archimedes is apparently satisfied with, and the notion of equality as absolute precision.
As developed theologically by St. Augustine, St. Thomas Aquinas, and Cusanus, God the Father is unity, the Son is equality, and the Holy Spirit the concord or the connection of the two. It is this notion of equality which was fought for at the Council of Florence.
Influence of Llull and Dionysius
In the 1420’s, Cusanus had travelled to Paris, where he gained access to the writings of Raymond Llull (1232-1316). Among the writings which Cusanus personally copied by hand, and can be found in Cusanus’s library, is a work entitled “On the Quadrature and Triangulation of the Circle,” written in June 1299. This work is important, because it begins with the statement that straight lines and circular lines are incommensurable, and that man cannot measure circular lines with straight lines.
This just underscores the fact that Cusanus was not the first to discover the incommensurability of a circular and a straight line. Cusanus’s discovery was to realize the implications of the incommensurability, i.e., that the circle is not incommensurable to the polygon in the same way that the diagonal of a square is incommensurable with its side. The circle is transcendental, and therefore ontologically superior, to the polygon, something which Llull did not realize.
The other major influence on Cusanus’s thinking about the difference between a circle and a polygon, as he himself writes in “On the Hunt for Wisdom,” was Dionysius the Areopagite (the “Pseudo-Dionysius”). Cusanus writes in “On Divine Names,” that Dionysius describes God as inaugmentable and irreducible. It is from this concept of the divine, that Cusanus derives his maximum-minimum—or isoperimetric—principle as characteristic of a circle.
This derivation of the isoperimetric principle from Dionysius is interesting historically. In Acts 17 of the New Testament, it is reported that the Apostle Paul travelled to Athens and spoke at the Areopagus on the Unknown God. He first attacked Epicurean and Stoic philosophers, and argued that the Mosaic God of Christianity is the Unknown God, in that He is not something created, and therefore finite, which can be known through the senses. After describing the Christian God, Paul cites a passage from one of the Greeks’ own poets, Aratus of Soli: “For we too are his offspring.” Paul then argues that since we are the offspring of God, we should not think of divinity as an idolatrous image fashioned from gold, etc. It is then reported that as a result of this speech, the individual Dionysius became a disciple of Paul.
Aratus, the poet cited by Paul, based his poem, entitled “Phenomena,” upon a prose work by the same name written by Eudoxus (390-337 B.C.E. ), the pupil of Plato, whose Eudoxian method was employed by Archimedes in attempting to prove the quadrature of the circle.
In the Fifth or Sixth century A.C.E. an unknown Platonic Christian adopted the pseudonym Dionysius the Areopagite. In his writings, including “On Divine Names,” this individual developed the idea of negative theology. As stated above, Nicolaus of Cusa applied this method in his investigation of the quadrature of the circle. In “On the Hunt for Wisdom,’ Cusanus writes:
But the great Dionysius asserts in the ninth chapter of “On Divine Names,” that that first Eternal is inflexible, inalterable, unmixed, immaterial, most simple, not indigent, inaugmentable, irreducible, has not become, is always existing ... .Thus, in making his breakthrough, Cusanus literally looked back over centuries to the School of Athens, to Plato’s pupil, Eudoxus, to Archimedes, to the Pseudo-Dionysius, and to Raymond Llull. And replicating the work that they had done, Cusanus was able to advance beyond Archimedes and Greek science, to develop the concept of a true infinite which is transcendent, because it transcends the domain of greater and less.I take two of these, namely, the inaugmentable and the irreducible, and hasten with them to the hunt, and I say that the inaugmentable cannot be greater; therefore, it is the maximum. The irreducible cannot be smaller; it is therefore the minimum. Hence, because it is equally the maximum and the minimum, it is in no way smaller, since it is the maximum, and in no way greater, since it is the minimum, but rather the most precise, formal, and exemplary cause and measure of everything great or small.
Impact on Kepler
The impact of Cusanus’s discovery on modern science is shown in Johannes Kepler’s (1571-1630) Mysterium Cosmographicum, Chapter II, “Outlines of the Primary Derivation”:
Now God decided that quantity should exist before all other things, so that there should be a means of comparing a curved with a straight line. For in this one respect, Nicolaus of Cusa and others seem to me divine, that they attached so much importance to the relationship between a straight and a curved line and dared to liken a curve to God, a straight line to his creatures; and those who tried to compare the Creator to his creatures, God to Man, and divine judgments to human judgments, did not perform much more valuable a service than those who tried to compare a curve with a straight line, a circle with a square.This passage from Kepler, who was the founder of astronomical science, not only establishes the contribution of Cusanus’s work on quadrature to the development of modern science. It also is a further confirmation of the importance of Christian theology, and in particular, the notion of God the Creator as triune, to scientific discovery. Both Nicolaus of Cusa and Kepler proceeded in their study of the physical universe on the basis of the Augustinian view that everything created by God contains a “trace” of the Trinity.And although under the power of God this alone would have been enough to constitute the appropriateness of quantities, and the nobility of a curve, yet to this was also added something else which is far greater: the image of God, the Three in One, in a spherical surface, that is of the Father in the center, the Son in the surface, and the Spirit in the regularity of the relationship between the point and the circumference. For what Nicolaus of Cusa attributed to the circle, others as it happens have attributed to the globe; but I reserve it solely for a spherical surface.
Kepler continues:
‘Only if a spherical surface or a globe is cut by a flat plane can a circle exist.This is the same principle which Cusanus develops in respect to the difference between a circle and a polygon. The polygon is derived from circular action. The circle cannot be attained from the standpoint of polygonal action. Similarly, circular action is derived from spherical action, which is a higher ontological order.
This concept of an ascending ontological order is developed by Nicolaus of Cusa in On Learned Ignorance, Book I, Chapter XII:
For since all mathematicals are finite and otherwise could not even be imagined: If we want to use finite things as a way for ascending to the unqualifiedly Maximum, we must first consider finite mathematical figures together with their characteristics and relations. Next, [we must] apply these relations, in a transformed way, to corresponding infinite mathematical figures. Thirdly, [we must] thereafter in a still more highly transformed way, apply the relations of these infinite figures to the simple Infinite, which is altogether independent even of all figure.
Archimedes’ Measurement of a Circle
With this introduction, let us now refer to Proposition 1 of Archimedes’ “Measurement of a Circle.” Cusanus wrote his “On the Quadrature of the Circle” in reference to this work. He also wrote three further pieces in response to Archimedes’ “On Spirals,” which was translated in 1453. These three additional works by Cusanus, were the “Quadrature of the Circle” (1453), the “Imperial Quadrature of the Circle”(1457), and a “Dialogue on Quadrature of the Circle” (1457). But since “On Spirals” employs the same method as his “Measurement of a Circle,” it is sufficient for the purposes of this paper to address Cusanus’s earlier treatment of the latter work.
Archimedes’ first proposition reads as follows:
The area of any circle is equal to a right-angled triangle in which one of the sides about the right angle is equal to the radius, and the other to the circumference, of the circle.
As we shall see, Archimedes’ proof of this proposition depends upon two propositions in Euclid’s Elements, which Archimedes attributes to Eudoxus. These two are Book X, Proposition 1 and Book XII, Proposition 2. These propositions reflect the Eudoxian “method of exhaustion” used by Archimedes.
Book X, Proposition 1 reads as follows:
Two unequal magnitudes being set out, if from the greater there be subtracted a magnitude greater than its half, and from that which is left a magnitude greater than its half, and if this process be repeated continually, there will be left some magnitude which will be less than the lesser magnitude set out.
|
Figure 2
|
Let AB and C be two unequal magnitudes of which AB is the greater [See Figure 2]:
|
Figure 3
 |
|
Figure 3(a).
Segments are shaded  |
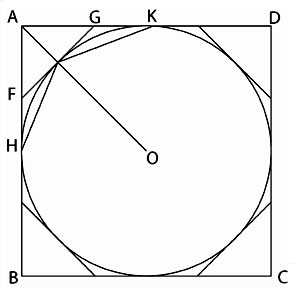
In Euclid’s Book XII, Proposition 2, this Eudoxian method of exhaustion is applied first to a polygon inscribed within a circle, and then to a polygon circumscribed around a circle. According to this proposition, we can exhaust a circle, in the sense of Book X, Proposition 1, by successively inscribing in it regular polygons, each of which has twice as many sides as the preceding one. We take an inscribed square, bisect the arcs subtended by the sides, and form an equilateral polygon of eight sides. We do the same with the latter, forming a polygon of 16 sides, and so on. As we shall see, what is left over when any one of these polygons is taken away from the circle, is more than half exhausted when the next polygon is made and subtracted from the circle. This is proven by the fact that the square is greater than half the circle, and the regular octagon, when subtracted, takes away more than half of what was left by the square.
Take an arc of a circle cut off by a chord AB [See Figure 3].
|
Figure 4
 |
|
Figure 4(a)
Sectors are shaded.  |
The same method is now used in respect to a polygon circumscribed around a circle [See Figure 4]. Suppose a square ABCD described about a circle. Make an octagon described about the circle by drawing tangents at the points E, etc., where OA, etc., meet the circle. Then the tangent at E cuts off more than half of the area between AK, AH, and the arc HEK. Thus, the octagon takes from the square more than half the space between the square and the circle. If continued enough times, the construction of successive regular polygons circumscribing the circle will leave sectors which are together less than any given area. (A sector is defined as the area outside of a circle cut off by two intersecting tangents [See Figure 4(a)].)
Now let us return to Archimedes’ proposition. Archimedes says, let ABCD be the given circle, [See Figure 5] and K the triangle described [See Figure 5a]. Then, if the circle is not equal to K, it must be either greater or less.
What Archimedes then does, is to prove that the circle cannot be either greater or less than K. First, he assumes that it is greater than K, and then, using the Eudoxian method of exhaustion, proves that it cannot possibly be greater. Then, assuming that it is less, he uses the same method to prove that it is impossible for it to be less. Then, since it is neither greater nor less than K, he concludes that it must be equal to it.
|
Figure 5.
 |
|
Figure 5(a)
 |
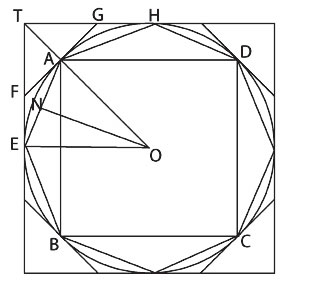
Let AE be any side of it, and ON the perpendicular on AE from the center O [See Figure 6]. Then, ON is less than the radius of the circle, and therefore less than one of the sides about the right angle in K. But, the perimeter of the polygon is less than the circumference of the circle, i.e., less than the other side about the right angle in K. Therefore, the area of the polygon is less than K; which is inconsistent with the hypothesis.
In the case where the circle is less than K, Archimedes directs: Circumscribe a square, and let two adjacent sides, touching the circle in E and H, meet in T [See Figure 7]. Bisect the arcs between adjacent points of contact and draw the tangents at the points of bisection. Let A be the middle point of the arc EH, and FAG the tangent at A. Then the angle TAG is a right angle. Therefore TG is greater than GA and greater than GH.|
Figure 6.
Detail of Figure 5 in respect to inscribed polygon. 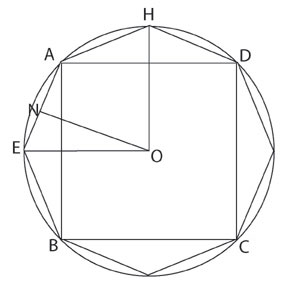 |
It follows that the triangle FTG is greater than half the area TEAH.
By continuing the process, we shall ultimately arrive at a circumscribed polygon, such that the sectors are altogether less than the excess of K over the area of the circle. Thus, the area of the polygon will be less than K.
However, since the perpendicular from O on any side of the polygon is equal to the radius of the circle, while the perimeter of the polygon is greater than the circumference of the circle, it follows that the area of the polygon is greater than the triangle K; which is impossible.
|
Figure 7 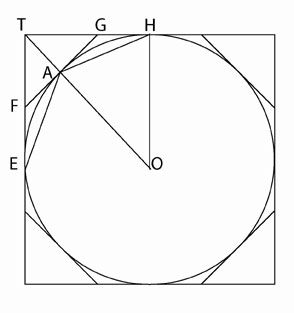 |
The ratio of the circumference of any circle to its diameter is less than 3 1/7 but greater than 3 10/71.
He arrives at the first value by circumscribing a circle with a 96-sided polygon, and the second value by inscribing a 96-sided polygon in a circle.
On the Quadrature of the Circle
It is clear that Nicolaus of Cusa is referring to Archimedes’ Proposition 1 in “On the Quadrature of the Circle.” At the beginning of his work, Cusanus writes:
There are scholars, who allow for the quadrature of the circle. They must necessarily admit, that circumferences can be equal to the perimeters of polygons, since the circle is set equal to the rectangle with the radius of the circle as its smaller and the semi-circumference as its larger side. If the square equal to a circle could thus be transformed into a rectangle, then one would have the straight line equal to the circular line. Thus, one would come to the equality of the perimeters of the circle and the polygon, as is self-evident.That Cusanus is referring to Archimedes here is clear from the second paragraph of his later work, “The Quadrature of the Circle,” where he writes, “We do not read that anyone has come nearer to the knowledge of the facts of this matter than Archimedes, who first pointed to the fact that a rectangle from the radius and the half-circumference of a circle, is equal to the area of the circle.” Since a right-angled triangle is half the area of a rectangle, Cusanus’s formulation of Archimedes’ proposition employs the semi-circumference with the rectangle, whereas the proposition as presented above employs the circumference with the right-angled triangle.
Cusanus begins his work with a proposition based upon the assumption of the validity of Archimedes’ proof. The proposition is as follows:
If to a given perimeter of a triangle an equal circular perimeter can be given, then the radius of this circle exceeds by one-fifth of its total that line, which is drawn from the center of the triangle to the point quartering the side from the corner.
In the course of the work, he will explain this proposition, and derive from it an approximate value for π . However, through this proposition he will simultaneously show why the value obtained is only approximate, and not precise. Before elaborating on this proposition, however, Cusanus proceeds to challenge the axiomatic assumptions underlying Archimedes’ work.
As Cusanus stresses, Archimedes’ proposition assumes that “Where one can give a larger and a smaller, one can also give an equal.” But, as Cusanus continues, there are those “who deny the possibility of the quadrature of the circle,” and they assert that “in mathematics, the conclusion does not hold, that where one can give a larger and a smaller, there one can also give an equal.”
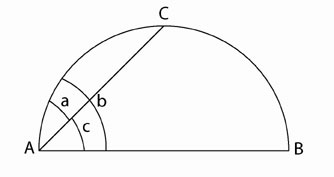
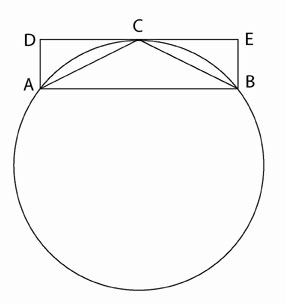
Then, Cusanus goes to the crux of the matter. He writes: “There can namely be given an incidental angle that is greater than a rectilinear, and another incidental angle smaller than the rectilinear, and nevertheless never one equal to the rectilinear. Therefore with incommensurable magnitudes this conclusion does not hold.” [See Figure 8]|
Figure 8.
The incidental angle b is greater than the rectilinear angel 3, and the incidental angel a is smaller than the rectilinear angel c. Yet, there is never an incidental angel equal to c. |
|
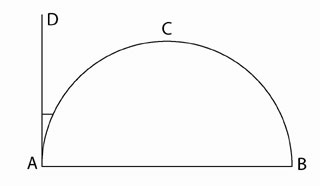
Figure 9.
The contingent, or conricular (horn-like) angle, DAC is the angle between the tangent AD and the semicircle ACB. |
Cusanus is raising an issue which has historically divided the scientific community. What he is pointing to, is the existence of a type of angle other than a rectilinear angle: the incidental angle of a segment, i.e., the angle inside a circle between the circumference and the line which cuts it off. This is referred to in Euclid in only one location, Book III, Proposition 16, as the “angle of the semicircle.” The other angle which Cusanus will refer to in “On the Quadrature of the Circle” is the contingent or cornicular (horn-like) angle [See Figure 9]. This is the angle between the circumference of a circle and the tangent. It is referred to in the same location in Euclid as “the remaining angle.”
Euclid’s Book III, Proposition 16 reads as follows:
The straight line drawn at right angles to the diameter of a circle from its extremity will fall outside the circle, and into the space between the straight line and the circumference another straight line cannot be interposed; further the angle of the semicircle is greater, and the remaining angle less, than any acute rectilineal angle.
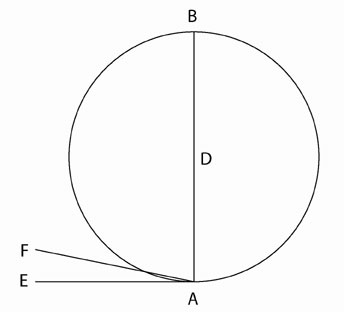
According to this proposition, if a straight line touches a circle at one point only, i.e., is tangent, then any other straight line which one attempted to interpose between that tangent and the circumference, would necessarily cut the circumference in two points, and thus fall within it [See Figure 10].
|
Figure 10
Straight line EA, at right angles to the diameter AB, is tnagent to the circle. No straignt line FA can be interposed into the space between the straight line EA and the circumference. Such a line FA would necessarily cut the circle in two locations, createing an incidental angle, rather than a contingent one. Therefore, the cornicular angle formed by the circumference and tangent EA is less than any possible rectinear angle. |
One of the most critical comments on Euclid’s Book III, Proposition 16 was made by Johannes Campanus, who edited Euclid’s Elements in the Thirteenth century. He inferred from III.16 that there was a flaw in the principle that the transition from the less to the greater, or vice versa, takes place through all intermediate quantities, and therefore through the equal. If a diameter of a circle, he says, be moved about its extremity until it takes the position of the tangent to that circle, then, as long as it cuts the circle, it makes an acute angle less than the “angle of a semicircle”; but the moment it ceases to cut, it makes a right angle greater than the same “angle of a semicircle.” The rectilineal angle is never, during the transition, equal to the “angle of a semi-circle.” There is therefore an apparent inconsistency with Book X, Proposition 1, and Campanus could only observe in explanation of the paradox, that “these are not angles in the same sense, for the curved and the straight are not things of the same kind without qualification.”
There is every reason to believe that Cusanus had access to Campanus’s edition of Euclid. Moreover, this is the same issue that Cusanus refers to in the passage in Book III, chapter I of On Learned Ignorance cited at the beginning of this article. Cusanus refers to this logical paradox as a “certain singularity.”
In 1557, the French geometer Peletier, argued that the “angle of contact” was not an angle at all. He claimed that the “contact of a straight line with a circle” is not a quantity, and that angles contained by a diameter and a circumference are all right angles and equal to rectilineal right angles. For Peletier, there was no difficulty with Euclid’s Book X, Proposition 1, because all angles of contact are not-angles, not quantities, and therefore nothings.
Vieta (1540-1603) agreed with Peletier that the angle of contact is no angle. His pseudo-proof was that the circle may be regarded as a plane figure with an infinite number of sides and angles; but a straight line touching a straight line, however short it may be, will coincide with the straight line and will not make an angle. In other words, if the circle is a straight line in the infinitely small, then there is no angle at the point of contact with the tangent.
Not surprisingly, this was also the view of Galileo Galilei (1564-1642).
This issue is in no way esoteric or academic; rather, it is one of the most profound issues confronting man. The cornicular angle is either equal to null, as the Aristotelians maintain, or it is virtually null, but nonetheless exists, and in fact has greater being and reality than the polygon which is derived from it. If the former is true, then the same argument can be made (and in fact has been made) theologically, that neither God nor the human soul exists. If the circle is no more than a polygon with an infinite number of sides, then God is equal to His creation (which is the basis of pantheism), and the soul is not immortal, but rather dies with the body.
This is the same issue as that which later divided Gottfried Wilhelm Leibniz (1646-1716) and Leonhard Euler (1707-83). Leibniz insisted that monads, or simple substances, are indestructible and indivisible. Euler, on the other hand, had lyingly argued that all magnitude is divisible to infinity.
To return to Nicolaus of Cusa’s argument: If one recognizes the existence of incidental angles, and understands that an incidental angle is not commensurable with a rectilinear angle, then it is clear that there can be no rational proportion between the area of a circle, and a rectilinearly enclosed area. As Cusanus writes:
If a circle can be transformed into a square, then it necessarily follows, that its segments can be transformed into rectilinearly enclosed figures. And since the latter is impossible, the former, from which it was deduced, must also be impossible. Obviously, then, the semicircle cannot be transformed into a rectilinearly enclosed figure, and consequently also not the circle or one of its parts.Similarly, Cusanus writes in respect to contingent or cornicular angles that, although they cannot be divided by another straight line, they are nonetheless divisible by another curved line: “The contingent angle is a divisible magnitude only in its species, since to every contingent angle there is a larger and a smaller contingent angle.”
Species Difference
Through this discussion of the incommensurability of incidental and contingent angles to rectilinear ones, Cusanus proves that the circle cannot be squared, because “polygonal figures are not magnitudes of the same species as the circular figure”:
In respect to things which admit of a larger and smaller, one does not come to an absolute maximum in existence and potentiality. Namely, in comparison to the polygons, which admit of a larger and smaller, and thereby do not attain to the circle’s area, the area of a circle is the absolute maximum, just as numerals do not attain the power of comprehension of unity and multiplicities do not attain the power of the simple.What is significant about this statement is, that Cusanus has identified the fact that the circle is of a higher power, or cardinality, than the polygon. The circle is a true infinite. As such, it does not admit of greater or less, as does the polygon. The area of the circle is thus simultaneously maximal and minimal. Moreover, it is in actuality all that it is potentially. The circle transcends the polygon in the same way that unity transcends numerals, and the simple transcends multiplicities. The latter cannot attain to the former; nonetheless, the former are present in the latter, as the cause is present in its effect.
Cusanus goes on to say that some consider the square equal to the circle, if it is not larger or smaller than the circle by the smallest specifiable fraction of the square or the circle:
If one apprehends the concept of equality in this way, then it is justly said that one can give an equal circumference to a given polygonal perimeter. However, if one apprehends the concept of equality, insofar as it relates to a magnitude, absolutely, without regard to rational fractions, then it is true that no precisely equal non-circular magnitude can be given for a circular magnitude.Cusanus now proceeds to explain his initial proposition. In demonstrating that a rational approximation of equality is possible, he at the same time shows why it is that one cannot know precise equality. He writes:
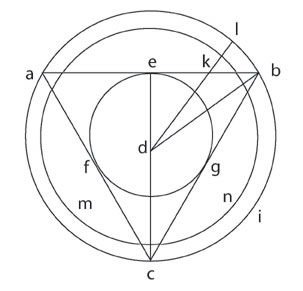
However, since this radius dl has no rational proportion to the circumference lmn, dl cannot be proportional to de or db. Nor is there commensurability between dl and dk or between dk and eb or db. As a result, therefore, of the incommensurability of the radius and the circumference of a circle, “no point on eb can be given, to which one could draw a line, which were precisely that sought.” Hence the best that one can do is to draw a line which is “most non-proportional to eb, de, and db” and this will be the “least non-proportional to the one sought.”In order to explain the proposition, a triangle abc shall be drawn [See Figure 11]; around the midpoint d shall be inscribed a circle efg, and a circle hi circumscribed; the straight line de shall be so drawn, that e is the midpoint between a and b; then db shall be drawn. Further, a straight line dk shall be drawn from d to the midpoint between e and b. I maintain: dk is smaller than the radius of the circle isoperimetric to the triangle, by one-fourth of the length dk.
Therefore, one must extend dk by a fourth of its total length, and indeed let dl be larger than dk by one fourth of dk. I maintain: dl is the radius of the circle of equal circumference to the triangle. One shall therefore describe the circle lmn. I maintain: The circumference lmn is equal to the circumference abc, and indeed such that lmn is neither larger nor smaller, not even by the very smallest rational fraction of the circumference abc.
In order to prove this assertion, I proceed in the following manner: I say, if it be possible, to draw a straight line from d to eb, that is the radius of the circle isoperimetric to the triangle, then it must be to the sum of the sides of the triangle, as the radius of the circle is to the circumference.
If, from the standpoint of the circle, the lines of the polygon are rendered incommensurable, we cannot determine with absolute precision the location of k such that the radius dl will be of the length sought.
|
Figure 12.
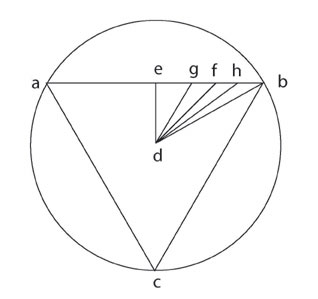 |
Once this is done, then one can derive a value for π . If db = 60, then ed = 30, eb = √2700, and the circumference of the triangle, which is equal to the circumference of the isoperimetric circle lmn, is 6 √2700.
Consequently, ek = √675 and dl = (5/4) √1575, the diameter of the isoperimetric circle 2 × dl = 2½ √1575. One then obtains the value of π by dividing the circumference 6 √2700 by the diameter 2½ √1575. The result is 3.1423376.
Having done this, Cusanus writes:
True, that is not the precise value, but it is neither larger nor smaller by a minute, or a specifiable fraction of a minute. And so one cannot know by how much it diverges from ultimate precision, since it is not reachable with a usual number. And therefore this error can also not be removed, since it is only comprehensible through a higher insight and by no means through a visible attempt. From that alone you can now know, that only in the domain inaccessible to our knowledge, will a more precise value be reached. I have not found that this realization has been passed along until now.In this passage, Cusanus self-consciously identifies the unique discovery he has made of a new type of number domain. As Lyndon LaRouche has pointed out, the Greeks had discovered incommensurability. They knew, for instance, that the diagonal of a square was incommensurable with the side. Archimedes believed that π was similarly an irrational magnitude. But what Cusanus established is that, whereas the relationship of the diagonal to the side of the square is irrational, the relationship of the circle to the square is transcendental. As LaRouche writes in Appendix A: “What Cusanus did was to recognize that π is not, ontologically, an irrational, but a number of a higher ontological type than irrationals, of a higher species.”
LaRouche continues in the same location: “Cusanus recognized that circular action: (a) could not be defined ontologically within the implicitly axiomatic formalities of Greek mathematics, since the circular perimeter, the locus of that action, was an absolute mathematical discontinuity between the two transfinite series, inscribed and circumscribed, of polygonal processes. (b) Moreover, since those polygonal processes themselves were externally bounded by circular constructions, the axiomatic formalities implicitly underlying Archimedes’ constructions could not access efficiently the ontological domain of circular action, but circular action could determine, and thus access efficiently the processes of the polygonal constructions’ domain. (c) Therefore, we must discard the implied set of axioms of Archimedes’ use of the Euclidean domain, and replace those with the axiomatic quality (Platonic hypothesis) of universal circular action (later, universal least action).”
On Learned Ignorance
After having thus superseded Archimedes by discarding his Euclidian axiomatic assumptions, Cusanus identifies the source of his discovery as his “learned ignorance”: “The measure with which man strives for the inquiry of truth has no rational proportion to Truth itself, and consequently, the person who is contented this side of precision does not perceive the error. And therein do men differentiate themselves: These boast to have advanced to the complete precision, whose unattainability the wise recognize, so that those are the wiser, who know of their ignorance.”
The concluding section of “On the Quadrature of the Circle” concentrates upon bringing out the theological implications of this discovery, which implications, as emphasized at the beginning of this article, are actually, self-reflexively, the source of the scientific breakthrough.
As Cusanus first made clear in On Learned Ignorance, the relationship of the circle to the polygon is a metaphor for the relationship between God and His creation, and in particular between God and man, who is created in His image.
Cusanus argues that “mathematical thinking has its seat in the true powers of the mind.” As a result, one can ascend from the study of finite mathematical forms to infinite mathematical forms and finally to an intellectual vision of the First Form, to the Absolute Form of forms. Thus, just as the circle’s area remains incommensurable to any area of a non-circle, so the infinite power of God is incommensurable to any non-infinite. As Cusanus writes:
Thus, just as the circle is a figurative perfection, comprehending every possible perfection of figures in itself, and just as its surface embraces the surfaces of all figures and has nothing in common with any other figure, rather is in itself perfectly simple and unique, so is absolute eternity the Form of all forms, which in itself encloses the perfection, and so its omnipotence encompasses all power of the forms, of every kind, but without having a commonality with any other form.Cusanus then makes an explicit comparison between the circle and the triune nature of God:
And just as the circular figure possesses, in the property of having neither beginning nor end, a certain similarity with eternity, and represents in its area, wherein it encloses the areas of all figures, a certain figure of omnipotence, and represents in the close connection with which it unites circumference and area, in a manner of speaking, a figure of the most loving and infinite connection, so we view in the divine essence the eternity, which in itself has omnipotence, and in both the infinite union. In eternity we view the beginning without beginning, and just this we name the paternal first cause. In the omnipotence, which comes from the beginning without beginning, we view the unbounded beginning from the beginning. In the infinite connection we view the most loving union of the beginning without beginning and of the beginning from the beginning. Namely in that we see eternity in the divine essence we view the Father. In that we see the power of eternity in the same essence, which cannot be other than infinite, since it is the power of eternity—of the beginning without beginning—, therein we view the equality of the eternal unity, that is, the Son of the Father. In that we see the most loving union of the eternal unity and its equality, we view the Spirit of them both. In the simplest unity of eternity we thus see the strongest and most powerful equality and conversely in equality, unity. Likewise, we also see unity and equality in the union.Although some may argue foolishly that this theological discussion is extraneous or irrelevant to Cusanus’s mathematical discovery, nothing could be further from the truth. It is precisely the Augustinian notion of the Son of God as “begotten, not made, consubstantial with the Father,” which gives Cusanus the idea of absolute equality, as distinct from the rational approximation of equality between the circle and the polygon accepted by Archimedes.
At the same time, as Lyndon LaRouche has pointed out, Cusanus’s scientific discovery that π is a transcendental number, is directly related to St. Anselm’s ontological proof of the existence of God.
Cusanus has shown that the circle is not null, but rather only virtually null. As such, it exists and is ontologically superior to the polygon, that is, all polygons are caused by circular action. Cusanus was not the first to realize that one cannot measure a circular line by means of a straight line, but he had the intellectual courage, because of his desire to attain the Truth itself, to realize the implication of this incommensurability.
The extent of Cusanus’s courage is better understood and appreciated, when it is realized that even today, 550 years after his discovery, the truth of that discovery continues to be denied by the Aristotelian heirs of Peletier, Vieta, and Galileo.
The Venetians and their pseudo-scientists have suppressed knowledge of Cusanus’s discovery, because they do not want you, the reader, to develop your own capacity for creativity; they do not want you to know that the capacity for creativity, which this discovery reflects, is the source of the progress which mankind has made during the 550 years since the Council of Florence. They realize that if you did come to master this method in your own mind, if you did become wittingly imago Dei, we would have the power to renew the face of the earth.
If we are to succeed in building a bridge from Hell to Purgatory in the apocalyptic period ahead, it will be because enough of us have refused to be “dumbed down,” and have accepted instead the challenge to master the crucial scientific discoveries of our predecessors, so as to better prepare ourselves to make the new, revolutionary discoveries necessary to continued human progress.
![]()
schiller@schillerinstitute.org
The Schiller Institute
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Thank you for supporting the Schiller Institute. Your membership and contributions enable us to publish FIDELIO Magazine, and to sponsor concerts, conferences, and other activities which represent critical interventions into the policy making and cultural life of the nation and the world.
Contributions and memberships are not tax-deductible.
VISIT THESE OTHER PAGES:
Home | Search | About | Fidelio | Economy | Strategy | The LaRouche Frameup | Conferences
Links | LaRouche | Music | Join | Books | Concerts | Highlights | Education |
Health | Spanish Pages | Poetry | Dialogue of Cultures
Maps | What's New
© Copyright Schiller Institute, Inc. 2006. All Rights Reserved.