
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps
Dialogue of Cultures
Non-Newtonian Mathematics
for Economists
by Lyndon H. LaRouche, Jr.
For related articles, scroll down or click here.
Non-Newtonian Mathematics for Economists
by Lyndon H. LaRouche, Jr.
| This article was originally published in Executive Intelligence Review, Vol. 22, No. 32, August 11, 1995, as a sequel to the author’s “Why Most Nobel Prize Economists Are Quacks” (Executive Intelligence Review, Vol. 22, No. 30, July 28, 1995). In that feature, the author referenced the reader to his relevant work on the issues of mathematical representation of the cause-effect relations characteristic of real economic processes. In the current work, he summarizes the method to be employed. | |||
Two problems must be addressed, in selecting a method of measurement for representing real economic processes. The primary task is to define a method for representing the physical-economic process as such: This process is characteristically “not-entropic.”1 The secondary, but also crucial task, is that of representing the interaction between that economic process and a superimposed, characteristically linear (and, therefore entropic) monetary and financial system.
The method required for representing the real economy, the physical-economic process, is described, step-by-step, as follows.
LaRouche’s Discovery
That original argument deployed against Wiener’s presumption, was that human “ecology” differs from that of lower species in the same general sense, that living processes differ characteristically from what we regard conventionally as non-living processes. This argument was premised on the fact, that the increase of the potential relative population-density3 of the human species, through such means as technological progress, represented a succession of clearly distinguishable phase-shifts: that these characteristic phase-shifts in the development of society, distinguish the human species absolutely from all lower species.
The initial representation of this distinction between mankind and the inferior species, was elementary: the standpoint of geometry. Any logically consistent form of mathematical mapping of an existing range of technology can be described, with effective approximation, in the form of a deductive theorem-lattice. Any valid discovery of a superior principle, has the effect upon mathematical physics, for example, of requiring a corresponding change in the set of formal and ontological axioms underlying the pre-existing, generally accepted form of mathematical physics. It is the cumulative succession of such efficiently progressive, axiomatic changes in human knowledge for practice, which corresponds to the succession of phase-shifts in range of society’s potential relative population-density.
This view defined an implied, functional ordering-principle underlying the increase of potential relative population-density. The initial thesis of the 1948-54 interval was, summarily, as follows. Let the physical and related consumption by households and the productive cycle, be regarded as analogous to the use of the term “energy of the system” in undergraduate thermodynamics. Societies rise or fall, in the degree to which they not only meet that “energy of the system” requirement, but also generate a margin of increased output of those qualities of requirement, which is analogous to “free energy.” We have thus, implicitly, a ratio of “free energy” to “energy of the system.”
An additional consideration is crucial. The development of society requires that a significant portion of that “free energy” be “re-invested” in the form of “energy of the system.” This must not merely expand the scale of the society; it must increase the relative “capital-intensity” and “energy-intensity” of society’s production, per capita and per unit of land-area employed. Thus, some minimal value of the ratio of “free energy” to “energy of the system” must be sustained, despite rising “capital-intensity” and “energy-intensity” of the mode used for the productive cycle. This constraint (array of inequalities) was employed to define the proper use of the term “negentropy,” in counterposition to Wiener’s use of the term. Recently, the term “not-entropy” was adopted as better serving this purpose [See Box on Relations of Measure Applicable to Physical Economy].
About 1949-50, the argument against Wiener assumed this form. Since the characteristic distinction of the human species is the series of phase-shifts in potential relative population-density, describable in this way: The ideas which are characteristic of the successful thinking of cultures, are those ideas represented efficiently as the changes in practice which tend to increase the potential relative population-density of the human species. It is this implicit social content of each valid axiomatic-revolutionary discovery in science or art, which defines human knowledge: not Wiener’s mechanistic, statistical approach.
It was already apparent, at that point in the investigation, that no conventional classroom mathematics was adequate for mapping this kind of “not-entropic” economic process. The central function of valid axiomatic-revolutionary ideas, locates the function of economic growth in the revolutionary changes in axioms as such. The mathematical problem so presented, is that changes in the sets of axioms underlying deductive theorem-lattices, have the form of absolute mathematical discontinuities. That is: There is no formal method for reaching the new lattice deductively from the old. Such a mathematical discontinuity has a magnitude of unlimited smallness never reaching actual zero. That implies the existence of very powerful, extremely useful sorts of mathematical functions, but no ordinary notion of mathematics can cope with functions which are expressed in terms of such discontinuities. To apply the writer’s original discovery, this problem of mathematical representation had to be addressed next. A mathematical solution would be desirable, but a conceptual overview was indispensable.
Thus, the next step, in early 1952, proved to be a study of Georg Cantor’s treatment of those kinds of mathematical discontinuities.4 The study of Cantor’s work on the subject of the mathematically transfinite, especially his so-called Aleph-series, pointed toward access to a deeper appreciation of the 1854 habilitation dissertation of Bernhard Riemann. Conversely, Riemann’s fundamental discovery respecting the generalization of “non-Euclidean” geometries, showed how we must think of Cantor’s functional notion of implicitly enumerable density of mathematical discontinuities per arbitrarily chosen interval of action.
That notion of relative density of discontinuities is the proper description of the culture which society transmits to its young.5 This notion of “density,” references the accumulation of those valid scientific and artistic discoveries of principle (e.g., valid axiomatic-revolutionary changes), which mankind to date has accumulated to transmit to the educational experience of the young individuals.
Once one recognizes that Cantor’s work is retracing the discovery made earlier by Riemann, there is an obvious advantage of choosing Riemann’s geometrical approach, over the relatively formalistic route used by Cantor.6 In the design of productive and related processes in modern economy, the conceptions which underlie the design of scientific experiments, and of derived machine-tool conceptions, are intrinsically geometric in nature. To think about production and economy, one must think geometrically, not algebraically.
Hence, the present writer’s use of Riemann’s work to address the mathematical implications of his own earlier discovery in economics, acquired the seemingly anomalous, but precisely descriptive name of the “LaRouche-Riemann Method.”7 Examine the most elementary of the relevant features of Riemann’s habilitation dissertation.8 For the purpose of clarity, the following passages repeat several of the points stated immediately above.
In the conclusion of his famous, 1854 habilitation dissertation, “On the Hypotheses Which Underlie Geometry,” Riemann summarizes his argument: “This leads us to the domain of another science, into the realm of physics, which the nature of today’s occasion [i.e., mathematics—LHL] does not permit us to enter.”9 In present-day classroom terms, that statement of Riemann’s has the following principal implications bearing upon the construction of a mathematical schema capable of adequately representing real economic processes.
Any deductive system of mathematics can be described as a formal theorem-lattice. A theorem in such a lattice is any proposition which is proven to be not inconsistent with an underlying set of interconnected axioms and postulates.10 The relevant model of reference for this notion of a theorem-lattice, is either a Euclidean geometry, or, preferably, the constructive type of geometry associated with the famous names of Gaspard Monge, Adrien M. Legendre, and Bernhard Riemann’s geometry instructor, Jacob Steiner.
This presents the difficulty, that any alteration within that set of axioms and postulates, generates a new theorem-lattice, which is pervasively inconsistent with the first. This inconsistency between the two, is expressed otherwise as a mathematical discontinuity, or a singularity. When defined in this proper way, to show the existence of such a discontinuity signifies, that no theorem of the second theorem-lattice can be directly accessed from the starting-point of the first, unless we introduce the notion of the operation responsible for the relevant change within the set of axioms.
In other words, we must depart pre-existing mathematics, and detour, by way of physics as such, to reach the second of the two mathematical theorem-lattices. The crucial term of reference which we must introduce at this juncture, as Nicolaus of Cusa prescribed in his work founding modern science,11 as Riemann does, is “measurement.”12 Consider this writer’s favorite, frequently referenced classroom illustration of the principle involved.
Consider the estimation of the size of the Earth’s polar meridian, by the famous member of Plato’s Academy of Athens, Eratosthenes; a measurement of the curvature of the Earth made during the Third centuryB.C.E.twenty-two centuries before any man was to have seen the curvature of the Earth.13 The twofold point to be made, is, briefly, as follows.
Using astronomy to determine a North-South line (a meridian of longitude), choose two points of significant, but measurable distance along that line, between them. Measure that distance. Construct identical sundials at each of the two points. Measure the shadow which a vertical stick casts, at noon on the same day, and compare the angles of the respective shadows. The difference between the two angles is adumbrated by the fact, that the Earth is not flat, but has a definite curvature [See Figure 1].
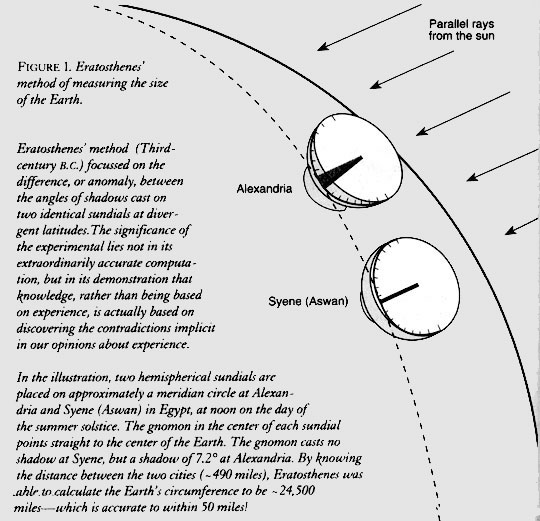
Using the geometric principle of similarity and proportion, estimate the size of the circle passing through the Earth’s two poles on the basis of the measured length of the arc-distance between the two points. Eratosthenes was off by about fifty miles, in estimating the polar diameter of the Earth.14
The two points illustrated by this example, are as follows.
First, this example illustrates what Plato signifies by an idea. Since this measurement was made twenty-two centuries before anyone had seen the curvature of the Earth, what was measured was not an object defined by sense-perception. The senses were employed, of course; but, the idea of curvature was derived from the certainty that the evidence of the senses was self-contradictory: The difference in the angles of the shadow at the two points was the empirical expression of that self-contradictory quality. It was necessary to go to conceptions which existed outside the scope of sense-perceptions: into the realm which Plato defines as that of ideas.15
Second, this, like related ancient Greek discoveries, leads into the modern geodesy developed by Riemann’s chief patron, Carl F. Gauss: the measurement of distances along the surface of the Earth, under the control of reference to astronomical measurements.16
Some reader might be tempted to object: “Why not say simply ‘trigonometry’; why use the term which is probably stranger to the layman, ‘geodesy’?” The critic would be committing a serious error, a type of error which is of direct relevance to the point at hand. Expressed as a recipe, the relevant rebuttal of the criticism is: We should always state what we claim to know in terms of the manner in which we came to know it. It is through recognizing, Socratically, that either we or those who taught us, might have overlooked a significant step of judgment actually taken, or omitted, in forming a conception, that crucial errors of assumption are uncovered, and corrected. More broadly, it is by reconsidering the way in which we acquired conceptions, by taking that process as an object of epistemological scrutiny, that a true scientific rigor is cultivated. In layman’s terms: that we might come to know what we are talking about.
We should define Eratosthenes’ act of discovery in the manner we might competently replicate it. It was through astronomy that Eratosthenes estimated the polar circumference of the Earth. He did this by methods which are related to the earlier proof, by Aristarchus, that the Earth orbited the sun, and, also, the methods by which Eratosthenes estimated the distance of the moon from the Earth, the latter a distance which no man was to have seen until about twenty-two-hundred years later. That is what we know in this matter; it should never be reformulated in a different fashion.
It is violations of our methodological prescription here, which are key to the way in which Isaac Newton, for example, stumbled into his fraudulent et hypotheses non fingo, and that numerous other frauds of Newton and his devotees were generated, and credulously adopted by later generations of students. As Riemann emphasized, contrary to Newton’s somewhat hysterical insistence that he made no hypotheses, Newton made a very obvious hypothetical assumption, on which his mathematical physics depends entirely. Riemann identified one aspect of that error;17 but one may apply the same method used by Riemann there, to show that the entirety of the Newtonian system, in the present-day classroom, rests upon that same fallacious hypothesis. Had Newton, or his followers, paid closer attention to the method by which the Newtonians actually reached the opinions which they claimed as their knowledge, they probably would not have dared continue such blunders, nor chant their ritual hypotheses non fingo.
Those who profess to know the answer because they looked it up in the back of the textbook, or because someone has told them, have merely “learned” that sort of answer, somewhat as a dog might have learned to retrieve a stick. Those who have not merely learned, but who know the answer, know it only because they have either made the original discovery, or have relived it, step by step. What we know—knowledge—is not the fruit of sense-certainty, but, rather, that which came to us through the rigorous demonstration of the kinds of ideas which could not be merely the interpretation of eyewitness observations. This point, respecting transparency of method, is the most obvious and crucial blunder of virtually all those generally accredited as economists, to date, who have claimed to address what is, in fact, such an ontologically complex subject-matter as the mathematical view of real economic processes.
For the competent economist, as for thoughtful physicists, the essential fraud of all empiricism, is: Akin to the traditional Aristoteleanism from which it is derived, empiricism insists that it addresses only the measurement of observed phenomena, free of the assumption of any governing hypothesis. This fraud is typified by Newton’s et hypotheses non fingo. Contrary to that fraud, the indispensable role of the continuing improvement of formal mathematics as such, is to provide more powerful instruments of analysis for testing the consistency of any given formal theorem-lattice. Economy of effort in science requires, that we be able to expose, more directly and quickly, the nature of inconsistency between the axiomatic basis underlying a theorem-lattice and some given, empiricist or other, presumption respecting how we ought to measure.18 Eratosthenes’ referenced measurement of the meridian is a simple illustration of that principle of science: the principle of scientific, i.e., Platonic, ideas.
In mathematics, or mathematical physics, such a Platonic form of idea is exemplified by the form of a set of axioms underlying any formal system, as what Plato and Riemann recognize as hypothesis. When we are speaking of formal theorem-lattice systems, such as a formal mathematics, “hypothesis” signifies the set of axiomatic assumptions underlying all provable theorems of a particular type of theorem-lattice (such as a Euclidean geometry, a linear algebra, etc.).19
- The pupil who had received a good secondary education, a Classical humanist form of such education, would already have mastered some of the precedents for this:
- He would be familiar, from the work of Plato’s Academy at Athens, and Archimedes, with the distinction between systems of mathematics limited to “commensurables,” and the so-called “incommensurables.”
- He would know Nicolaus of Cusa’s conclusive proof of the division of the domain of the “incommensurables,” between what we term the “irrationals” and the “transcendentals.” In his introductory education in the calculus, that student would also have come to understand how Leibniz and Jean Bernoulli showed the incompetence of Descartes’ and Newton’s “algebraic methods” (e.g., “infinite series”), and why, from the standpoint of the physics of refraction of light, “algebraic” methods must be replaced by “non-algebraic,” or “transcendental” notions of mathematical function.
- He might also know, that the emergence of the notion of the Riemann Surface function and Cantor’s Aleph-series, is traceable from those notions of mathematical discontinuities central to the mathematical work of Cusa and Leibniz’s articulation of a differential calculus, the notion of discontinuities hysterically denied by Newton devotee Leonhard Euler.
In each historical case, such as the subsumption of all notions of magnitude under the generalization of “incommensurables,” mathematics undergoes an axiomatic change within its underlying assumptions, its hypothesis. So, by the proof, cued to Ole Rømer’s crucial measurement of the speed of light, of the experimentally demonstrable nature of generalized refraction of light, Leibniz and Bernoulli established the domain of the transcendental, as earlier demanded by Nicolaus of Cusa, who introduced the isoperimetric principle,20 this the axiomatic basis for the mathematics of the transcendental domain. The linear hypothesis of Euclidean space-time (axiomatic self-evidence of points and lines), was superseded by the principle of the cycloid: a space-time in which (Cusa’s) isoperimetricism, least time, and least action govern in a unified way.21 The Riemann Surface function, and Cantor’s Aleph-series, implicitly define a physical universe in which the existence of not-entropic (e.g., living and cognitive) processes is not merely permitted, but necessary. Riemann’s habilitation dissertation, his work on the Riemann Surface, upon plane air waves, and so on, all address this historical evolution of the notions of geometry under the impact of those ideas erupting from the domain of physics.
For the economist, the crucial point is, that economic processes exist only within the last of the types of geometry we have just listed: that of not-entropic processes, of the process of mankind’s increasing domination of the universe: per capita, per family household, and per relevant unit of the Earth’s surface area. That domination signifies, that the universe we are addressing is, itself, a not-entropic process. Any mathematics not appropriate to this sort of not-entropic process, is intrinsically incompetent for economic analysis.
Eratosthenes’ referenced discovery, like related discoveries, implies a qualitative change in the way we should think about measuring differences along the surface of the Earth, and also the way in which astronomical observations are read. The corroborating differences in measurement to which we are led, axiomatically, by those ideas, posed in that way, reflect the efficiency of such a discovery: the proof of any axiomatic-revolutionary, or related discovery, is not its apparent formal consistency with an existing mathematics, but, rather, that it increases the human species’ power in the universe.
The referenced examples of changes in types of mathematics, illustrate the point. As illustrated by the Eratosthenes case, once that type of proof of an idea is obtained, we must then modify the axioms of geometry to such effect that we have constructed a new mathematics, a new theorem-lattice. This step takes us into the midst of the discovery which Riemann presents in his habilitation dissertation.
Riemann’s Discovery
Mathematics, all geometry included, is not a product of the senses, but of the imagination. In the principal part, our mathematics are rooted within the ideas of geometry; what most persons, including professional devotees of the Galileo-Newton tradition, consider mathematics, is derived from a naive conception of simple Euclidean solid geometry. Now focus upon a more narrowly defined aspect of the general problem so posed: the fallacies inhering in the attempt to construct mathematical economic models on the basis of a Newtonian form of today’s generally accepted university-classroom mathematics.
That mathematics is derived from a special view of a conjectured Euclidean model for space-time. That space is assumed to be ontologically an empty space, defined by three senses of perfectly continuous, limitless extension: up-down, side-to-side, and backward-forward. This space is situated within a notion of time, as also perfectly continuous extension, in but one sense of direction: backward-forward. This can be identified usefully as a notion of geometry derived from the naive imagination. Those four senses of perfectly continuous, limitless extension (quadruply-extended space-time) constitute the distinguishing hypothesis of that geometry as a theorem-lattice.
To this is added a simplistic notion of imaginary physical space-time, which might be fairly described, otherwise, as “Things do rattle about if placed in an otherwise empty bucket.” Given, an object, assumed to correspond to an actual or possible sense-perception. According to the hypothesis for simple space-time, a point, whose intrinsic space-time size is absolute zero, can be located as part of that object, and also as a place in quadruply-extended space-time. Extending that notion, any object can be mapped as occupying a relevant region of space-time; this mapping is done in terms of a large density of such points common, as places, to the object, and to space-time.
It is assumed, next, that motion of objects can be tracked in this manner (in quadruply-extended space-time). However, physical experience shows that space-time alone could not determine the motion of objects. The variability in the experienced motion, is assumed to correspond to what we may term physical attributes, such as mass, charge, smell, and so on. The notion of extension can be applied to each of these attributes. This prompts us to think of physical space-time, to think in terms of multiply-extended magnitudes in a way which is more general than the intuitive notion of simple space-time.
If it is adopted as part of the hypothesis for the system, that apparent cause-effect relations affecting motion can be adequately expressed in terms of manifold such assumedly physical factors of extension, the result of such attempted constructions of a physical space-time, is describable as an assumed physical space-time manifold. That geometry of the naive imagination, is the general map for the empiricist mathematical physics of Paolo Sarpi and such of his followers as Galileo Galilei, Francis Bacon, Thomas Hobbes, René Descartes, Isaac Newton, Leonhard Euler, Lord Rayleigh, and so on.24
That simplistic approach to mathematical physics, is the implicit basis for what are, presently, generally accepted notions bearing upon economics, both within the profession, and among illiterates, alike. This mechanistic schema of the Newtonians, is otherwise the pervasive misconception of the term “science” itself. This is the customary referent for use of the cant-phrase “scientific objectivity.”
Riemann introduces this consideration in the two opening paragraphs. He attacks the problems of that naive geometry itself, thus:
It is known, that geometry presupposes both the conception of space, and the first principles for constructions in space, as something given. It gives only nominal definitions, while the essential determinations appear in the form of axioms. The relation of these presuppositions remains in darkness; one has insight neither, if and how far their connection is necessary, nor, a priori, if they are possible. From Euclid to Legendre, to name the most famous of recent workers in geometry, this darkness has been lifted neither by the mathematicians, nor by the philosophers who have busied themselves with it. ... A necessary consequence of this [the foregoing considerations—LHL], is that the principles of geometry cannot be derived from general notions of magnitude, but rather that those properties, by which space is distinguished from other thinkable three-fold extensions of magnitude, can be gathered only from experience.25
Or, as Riemann puts the latter point at the conclusion of the same dissertation, within “the domain of physics,” as distinct from mathematics per se.26
The first mathematical challenge posed by the mere general idea of a physical space-time manifold is embodied in the fact, that such an idea precludes all notions of a static geometry. Since the close of the last century, it has been noted frequently, that once we take into account the fact, that we can not reduce the variability of velocities of motion, among even simple objects, to some principles of bare space-time, the bare notions of space and time must be expelled from mathematical physics.27 Since our notions of mathematics are derived from the three-fold space of our imagination, how shall physics account mathematically for the distortion which the evidence of a physical space-time manifold imposes upon the possibility of representing motion in space-time?
Let us interrupt the description of Riemann’s dissertation briefly, to inform the reader that, in the next few paragraphs, we are now about to address, not all of the crucial points of the dissertation, but several which all bear implicitly upon the problems of “economic modelling”; one of these most explicitly.
In addressing the first of a series of implications, on the concept of an n-fold extended magnitude,28 Riemann states he has found but two existing literary sources which have been of assistance to him: Gauss’ second treatise on biquadratic residues,29 and a philosophical investigation of Johann Friedrich Herbart.30 Then, in the opening paragraph of the next subsection, on the relations of measure,31 he states a crucial point on which our attention will be fixed: “Consequently, if we are to gain solid ground, an abstract investigation in formulas is indeed not to be evaded, but the results of that will allow a representation in the garment of geometry. ... [T]he foundations are contained in Privy Councillor Gauss’ treatise on curved surfaces.”32 Let the echo of “a representation in the garment of geometry” resonate throughout reflections upon what now follows.
In 1952, when the writer re-read this Riemann dissertation in the light of Cantor’s Aleph-transfinites, the writer’s own relevant form of “relations of measure,” was already the same principle of measurement subsumed by that same general conception of physical-economic “not-entropy” described here. Define the “not-entropy” of a physical-(macro)economic process in the general terms employed above. Consider the following preparatory steps required for broadly defining the meaning of “relations of measure” applicable to such an economic process.
Assign some small, but significant “free energy” ratio, such as the suggested five percent figure. This ratio subsumes the following included inequalities: The potential relative population-density, must rise; the demographic characteristics of family households and of the population as a whole, must improve; the capital-intensity and power-intensity, measured in physical terms, must increase, per capita, per household, and per unit of relevant land-area employed; a portion of the “free energy” margin sufficient to sustain a value constantly not less than five percent free-energy ration, must be reinvested in the productive cycle, to the effects of increasing the capital-intensity, the power-intensity, and the scale of the process [See Box on Relations of Measure Applicable to Physical Economy]. The requirement of the constant five percent growth-factor, serves as a rule-of-thumb standard, to ensure that the margin of growth is sufficient to prevent the process from shifting, as a whole, into an entropic phase.
Those are the effective relations of measure characteristic of successful national economies. Adopting those relations of measure, to what sort of physical space-time are we implicitly referring? Look back to the earlier history of development of modern science; there, one encounters some useful suggestions.
The founding work of modern science, Nicolaus of Cusa’s De Docta Ignorantia, introduced the notion in the form of a self-subsisting process, the isoperimetric principle, to supersede the axioms of point and straight line. This isoperimetric principle, in the guise of the cycloid of generalized refraction of light, became associated with the notions of “least action,” “least time,” and “least constraint.” From the referenced work of Rømer and Huyghens, through Jean Bernoulli and Leibniz, and beyond, the notion of a principle of retarded propagation of light, as associated with the isoperimetric principle, etc., has served as the yardstick, the “clock,” of relative value for physical science in general. Now, noting that, define the motion of a not-entropic economic process relative to the measure provided by the “clock.”
As measured by that “clock,” we measure, in first approximation, the relations of production and consumption in societies taken as integrated entireties. This is a statistical beginning, but not the required standard of measure. These first estimates must be expressed in a second approximation, in terms of rates of change of the relations of production and consumption; that, in turn, must be expressed as rates of increase of potential relative population-density.
This, in turn, requires that we re-examine the notion of economic not-entropy. The content of the not-entropy is not measured in terms of the increase of the numbers of market-basket objects, and of the ratio of production to consumption. Rather, the validity of efforts to measure performance in those market-basket terms, depends upon the coherence of that estimate with increase of the potential relative population-density. In other words, economic not-entropy, expressed as we have described its statistical approximation above, must parallel increase of the potential relative population-density. It is the increase of the potential relative population-density, as such, which is the ontological content of the not-entropy being estimated.
So, instead of measuring distance in physical-economic space-time in centimeter-gram-second, or analogous qualities of units, we measure that not-entropic effect expressed as increase of potential relative population-density. The value of the action is expressed implicitly in the latter measure. As we wrote, near the outset here: It is the implicit social content of each valid axiomatic revolutionary discovery in science or art, which defines human knowledge: not Norbert Wiener’s mechanistic, statistical approach. That implicit social content, is the efficiency of practiced ideas, to the effect of maintaining and also increasing the rate of increase of society’s potential relative population-density.
Consider the implications, for mathematics, of the points we have just summarized.
The first step in constructing a “physical-economic space-time manifold,” uses the countable categories of items indicated for such statistical studies. That second step is to employ that data-base to provide a means of measuring relations within the system in terms of the estimated relative not-entropy of the ongoing economic process as an integrated entirety. The third step, is to estimate the rate of not-entropy, as checked with and corrected by a comparison with the rate of not-entropy expressed in terms of potential relative population-density. The third step’s results must be reflected, as correction, upon the standards earlier estimated for the second step; that latter correction, must, in turn, be reflected upon the valuation of the statistical categories employed in the first step. Riemann’s work provides a conceptual guide for that multifacetted effort.
By introducing the principle, that relations of measure in physical-economic space-time are governed by the principle of rate of increase of potential relative population-density, we have located the mathematical representation of economic processes within non-Euclidean geometry, as Riemann’s dissertation defines the notion of such a geometry. To wit: In the graphs which we are able to construct, using appropriate market-basket data, we have embedded our standard of measure.
In Eratosthenes’ time, to the eye of the observer, the Earth was flat, and, therefore, it must be measured according to what passed for principles of plane geometry at that time. By showing that method of measurement to lead to a devastating contradiction, if regarded in a certain way, Eratosthenes required what became known later as principles of geodesy to be employed—the principles governing measure in curved surfaces, in place of the standards of plane geometry.
As we noted, above: Later, during the last quarter of Europe’s Seventeenth century, once the astronomical researches of Ole Rømer had established a definite rate for retarded propagation of light radiation, the combined work of Huyghens, Leibniz, and Jean Bernoulli established the necessity for replacing the naive, Sarpi-Galileo form of perfectly continuous Euclidean space-time by a physical space-time of five-fold extension, a space-time which, according to Leibniz, was not perfectly continuous.33 In addition to quadruply-extended space and time, the rate of retarded propagation of light must be added as another extension. To reflect that, it was necessary to adopt Cusa’s notion that the idea of triply-extended space must be subordinated to what Cusa was first to define, what was later named the transcendental domain, in which the isoperimetric principle, rather than axiomatic points and lines, defines the hypothesis underlying measure.
And, so on, in history since then.
In that tradition, aided by Riemann’s work, we are able to present the geometric shadow of the corresponding n-fold physical space-time manifold of physical economy, as an image in a triply-extended domain. Which is as if to say with the 27-year-old Riemann,34 that “an abstract investigation in formulas is indeed not to be evaded, but the results of that will allow a representation in the garment of geometry.” The essential qualifications are, that we must never forget that that is precisely what we have done.35
To understand the relevant contribution by Riemann in the degree required for our purposes here, we must return to read Riemann in the very special way this writer re-read Riemann’s dissertation back in 1952. We must focus upon the specificity of that deeper insight into Riemann’s discovery which had been prompted by this writer’s study of Cantor’s work.
Density of Discontinuities
Briefly, among the historical-philosophical observations, Cantor identifies his notion of the transfinite to be coincident with Plato’s ontological notion of Becoming, and his notion of the mathematical Absolute to be coincident with Plato’s ontological conception of the Good. For the application of this to Riemann’s discovery, the relevant issues are summarily implicit in Plato’s Parmenides dialogue. The case in point is as follows.
In the Parmenides, Plato’s Socrates lures Parmenides, the leader of the methodologically reductionist Eleatic school, into exposing the inescapable and axiomatically devastating paradoxes of the Eleatic dogma. The paradox is both formal and ontological, most significantly ontological. In the dialogue itself, Plato supplies only an ironical, passing reference to the solution for this paradox: Parmenides has left the principle of change out of account. The functional relationship of Plato’s implicit argument to Riemann’s discovery, is direct; Cantor’s references to Plato’s Becoming and Good, are directly relevant to both. Riemann himself supplies a significant clue to these connections, in a posthumously published, anti-Kant document presented under the title “Zur Psychologie und Metaphysik.”40
The relevant aspects of the common connections are essentially the following.
Reference the stated general case of a series of theorem-lattices, considered in a sequence corresponding to increases in potential relative population-density of a culture. We are presented, thus, with a lattice of theorem-lattices, each separated from the other by one or more absolute, logical-axiomatic discontinuities (e.g., mathematical discontinuities). Question: What is the ordering relationship among the members of such a lattice of theorem-lattices? Consider this as potentially an ontological paradox of the form treated by Plato’s Parmenides.
Some discoveries may occur, in reality, either prior to or after certain other discoveries; however, they must always occur after some discoveries, and prior to some others. This is true for discoveries in the Classical art-forms and related matters, as for natural science. In other words, each valid axiomatic-revolutionary discovery in human knowledge, is identifiable as a term of the lattice of theorem-lattices, exists only by means of a necessary predecessor, and is itself a necessary predecessor of some other terms. This is the historical reality of the cumulative valid progress in knowledge, to date, of the human species as a whole. This is, for reasons broadly identified above, the function which locates the cause for successive increases in mankind’s potential relative population-density. Question: What is the ordering-principle which might subsume all possible terms of this lattice of theorem-lattices?
On the relatively simpler level, if the series of terms being examined is of a certain quality, the solution to the type of paradox offered in the Parmenides is foreseeable. If the collection of terms can be expressed as an ordered series, or an ordered lattice, the terms can be expressed as either all, or at least some of the terms generated by a constant ordering principle, a constant concept of difference (change) among the terms. In that case, the single notion of that difference (change) may be substituted for a notion of each of the terms of the collection. In terms of the Plato dialogue, the Many can be represented, thus, by a One.
Cantor’s principal work is centered upon the case of the representation of the Many of an indefinitely extended mathematical series, by a One. The treatment of the notion of mathematical cardinality in this scheme of reference, leads toward the notion of the higher transfinite, the Alephs, and to the generalization of the notion of counting in terms of cardinalities as such. The latter corresponds, most visibly, to the idea of the density of formal discontinuities represented by compared accumulations of valid axiomatic-revolutionary discoveries. Question: How is the latter Many to be represented by a constructible, or otherwise cognizable One?
The notion associated with the solution to that challenge is already to be found in the work of Plato: the notion of higher hypothesis. However, using the terms from Riemann’s dissertation, the conceptualization of this solution, actual knowledge of this notion of higher hypothesis, as an ontological actuality, “will be gathered only from experience.”
Consider the case of the student who has been afforded that Classical-humanist form of education, in which reliving the act of original axiomatic-revolutionary discoveries of principle, is the only accepted standard for knowledge. That student has the repeated experience of applying a principle of discovery which leads consistently to valid axiomatic-revolutionary discoveries. That repeated experience, that reconstructed mental act of discovery, has been rendered an object—an idea—accessible to conscious reflection, an object of thought. Like any such object of thought, that state of mind can be recalled, and also deployed. How should we name this quality—this type41—of thought-object?
Just as Plato identifies a valid new set of interdependent axioms, underlying a corresponding theorem-lattice, as an hypothesis, so he references the type of thought-object to which we have just made reference as an higher hypothesis. The fact that the mode of effecting valid axiomatic-revolutionary hypotheses may be itself improved, signifies a possible series of transitions to successively superior (more powerfully efficient) qualities of higher hypothesis, a state of mental activity which Plato’s method recognizes as hypothesizing the higher hypothesis. The latter is congruent with Cantor’s general notion of the transfinite; in other words, Plato’s ontological state of Becoming.42
In the posthumously published paper, “Zur Pyschologie und Metaphysik,” Riemann identifies both “hypothesis” and “higher hypotheses” as of a species he names Geistesmassen. This term is synonymous with Leibniz’s use of “Monad,” and the present writer’s preference for the term “thought-object”: ideas which correspond to the types of formal discontinuities being considered here. Every person who has re-experienced, repeatedly, valid axiomatic-revolutionary discoveries in the Classical-humanist manner referenced, is familiar with the existence of such ideas.
Now, that said, back to Plato’s Parmenides. Consider the case, that the principle of change, the One, ordering the generation of the members of the collection, the Many, is of the form of higher hypothesis. This is the case, if the members of the collection termed the Many, each represent valid axiomatic-revolutionary discoveries. Contrary to Kant’s Critiques,43 the principle of valid axiomatic-revolutionary discovery is cognizable, and that from the vantage-point already identified here.
Also, contrary to Kant’s notorious Critique of Judgment, the same principle governs Classical forms of artistic creativity: as in the history of the pre-development of the method of motivic (modal) thorough-composition. The discoveries associated with this form of creativity are exemplified by Mozart (1782-86) and by Beethoven’s revolution in motivic thorough-composition, as exemplified by the late string quartets.44 Johannes Brahms is also a master of that method of coherent musical creativity.
The immediately foregoing several summary observations serve to indicate the accessibility of the notion of a comprehensible ordering of a lattice of theorem-lattices. Relative to the economic-theoretical implications of Riemann’s dissertation, the point to be added here, is that this notion is not only intrinsically cognizable. This is a physically efficient notion, and is ontological in that sense. It is also ontological in a sense supplied earlier by Heracleitus and Plato.
The question is at least as old as these two ancient Greeks.
Once the ontological issue of Plato’s Parmenides is taken into consideration, the following question is implicitly posed. The subsuming One is a perfect expression for the domain typified by the subsumed Many. Consequently, does the ontologically intrinsic, relative imperfection of that Many signify that the ontological actuality reposes in the One, rather than the particular phenomena, or ideas of the Many? The One always has the content of change, relative to the particularity of each among the Many. Does this imply that that change is ontologically primary, relative to the content of each and all of the Many? In other words, is this ontological significance of Heracleitus’ “nothing is constant but change” to be applied?
That is the type of significance which the term “ontologically transfinite” has, when applied to the formally or geometrically transfinite orderings presented, respectively, by Cantor and Riemann’s dissertation.
Put the same proposition in the context of physical-economic processes.
Let the term “lattice of theorem-lattices” identify an array of theorem-lattices generated by a constant principle of axiomatic-revolutionary discovery: an higher hypothesis. Then, that higher hypothesis is the One which subsumes the Many theorem-lattices. Relative to any and all such theorem-lattices, it is that higher hypothesis which is, apparently, the efficient cause of the not-entropy generated in practice. It is that higher hypothesis which is (again: apparently) the relatively primary, efficient cause of the not-entropy. It is that higher hypothesis, which is, relatively primary, ontologically.
As Leonhard Euler, and, later Felix Klein,45 refused to take into consideration: Correlation, even astonishingly precise correlation, is not necessarily cause. The cause is not the formal not-entropy of such a lattice of theorem-lattices; the cause is expressed in those hermetically sovereign, creative powers of each individual person’s mental processes: the developable potential for generating, receiving, replicating, and practicing efficiently the axiomatic-revolutionary discoveries in science and Classical art-forms. This notion of causation, drawn from “experience,” is the crux of the determination of a Riemannian physical-economic space-time.
Mankind’s success in generating, successfully, upward-reaching phase-shifts in potential relative population-density, demonstrates that the universe is so composed, that the developable creative-mental potential of the individual human mind is capable of mastering that universe with increasing efficiency. On this account, the very idea of “scientific objectivity” is a fraud, particularly if expressed as an empiricist, or “materialist” notion. All knowledge is essentially subjective; all proof is, in the last analysis, essentially subjective. It is our critical examination of those processes of the individual mind, through which valid axiomatic-revolutionary discoveries are generated, or their original generation replicated, which is the source of knowledge. This is shown to represent a valid claim to knowledge, at least relatively so, by the success of axiomatic-revolutionary scientific and artistic progress, in increasing mankind’s potential relative population-density. It is through the critical self-examination of the individual mental processes through which such discoveries are generated, and their generation replicated, that true scientific knowledge is attained: the which, therefore, might be better termed “scientific subjectivity.”
Notably, valid axiomatic-revolutionary discoveries can not be “communicated” explicitly. Rather, they are caused to reappear in other minds only by inducing the other person to replicate the process of the original act of discovery. One may search the medium of communication for eternity, and never find a trace of the original communication of such an idea to any person. What is communicated is the catalyst which may prompt the hearer to activate the appropriate generative processes within his or her own fully autonomous creative-mental processes. The result may thus appear, to the “information theorist,” to be the greatest secret code in the universe: In effect, by this means, the means of a Classical-humanist mode of education, vastly more “information” is transmitted than the band-pass is capable of conducting.
Thus, the following:
- The cause of the not-entropic characteristic of healthy physical-economy, is the exercise of the developable and sovereign mental-creative potential of the individual human mind. It is the input to that potential, which produces the efficient not-entropy as an output.
- The crucial social part of the process is the correlated form of individual potential for being stimulated to replicate the relevant act of discovery.
- The human precondition, is the development of the individuals and their relations within society to foster this generation and replication of such ideas.
- The efficient practice of this social process depends upon the preparation of man-altered nature to become suitable for the successful (not-entropic) application of these discoveries to nature.
Those are the axioms governing that causation essential to the geometry of physical-economic processes. The not-entropic image of an implied cardinality function in terms of densities of singularities per chosen interval of relevant action, is the reflection of those axioms and their implications. The set of constraints (e.g., inequalities), governing acceptable changes in relations of production and consumption, must therefore be in conformity with such a notion of a not-entropic cardinality function: that set of inequalities must be characteristically not-entropic in effect.
As was noted near the outset here: A mathematical solution (in the formal sense) would be desirable, but a conceptual view was indispensable. The most important thing, is to know what to do. Above all, we must be guided by these considerations in defining the policies of education and popular culture which we foster and employ for the development of the mental-creative potential of the individual in society, especially the young.
Epilogue:
The Interaction Principle
There are three typical states to be considered:
- The two processes, the monetary-financial parasite and the physical-economic process, are “symbiotically” inter-linked, with the parasite dominant, but with such constraints that a phase-shift of the economic process into an entropic mode does not occur;
- The two processes are similarly linked, but the dominating monetary-financial process progressively de-couples itself from the economic process; and
- The physical-economic process is employed by government to regulate the monetary and financial process to such a degree, that the latter becomes a subsidiary institution of the former.
The first, was what might be termed the “normal” state of symbiosis within the industrialized economies, during the several centuries preceding 1963. The second, is the presently, hyperbolically degenerating state of the combined world economy and monetary-financial systems. The third, is the preferred arrangement, implicitly defined by the George Washington administration of the U.S. Federal republic: the so-called “model” represented by the Franklin-Hamilton-Carey-List “American System of political-economy.”46
The crucial issue of the interaction, is the role of the sovereign nation-state form of national economy. “Experience,” in Riemann’s referenced sense of Erfahrung, informs us that the achievement of the most desirable, third form of interaction requires a strong role of a sovereign nation-state’s government in the economy. The U.S.A.’s historical experience clearly indicates what the outlines of those governmental functions, on several levels, must be.
The national government must retain sovereign responsibility for regulation of the currency and national credit, monetary, and financial affairs generally, and conditions of trade. This sovereign authority must be applied most emphatically to international affairs, and, as may be deemed necessary for national economic security, in some limited aspects of domestic commerce. Government, at the various national, regional,47 and local levels, must assume responsibility for providing essential basic economic infrastructure, including measures to ensure adequate quality of universal education, health-care delivery, and promotion of scientific and technological progress.48
It is desirable that the preponderance of remaining economic activity be accomplished through privately owned farms and other enterprises. The economic principle governing this is encountered as early as the Fifteenth-century France of Louis XI, and, more generally, in the nation-states of western Europe. Exemplary of those origins of the modern private enterprise, is the use of governmental patents to grant limited-term monopolies on manufacture and sale to inventors and their business associates; this is the origin of the limited-term, modern patent issued to inventors. The social function of private ownership, is to foster the application of the creative powers and intellectual prudence and courage of the individual entrepreneur, as a person, to the fostering of the generation and efficient use of improvements in methods and practices to the economic advantage of the nation and humanity more generally.
The division of authority and responsibility between the state and the private entrepreneur, is defined essentially by the nature of the social responsibilities implicitly assumed, or neglected by each. The development of basic economic infrastructure, represents the requirement, that a responsibility be met to the entire land-area of the relevant political unit, to the population considered as a whole, and to those general matters in which only government can assume efficient direct responsibility. Within the framework of governmental responsibility to provide or to regulate, the private entrepreneur should enjoy a broad, if nonetheless delimited authority.
That is not, as some misguided ideologues would describe it, a “mixed economy”; it is the only sane construction of a modern economy.
The most efficient performance of national economies has been achieved through what President Charles de Gaulle’s France knew as “indicative planning.” The state employs its combined monopolies of regulation and scale of economic operations, to foster the rate of investment and growth in those projects and other special categories of enterprise, which will supply the relatively greatest rate of well-balanced growth of the economy as a whole. The use of national credit, to foster beneficial and needed public works, and large-scale science-driver programs, such as aerospace development ventures, are typical of the strategic uses of concentrating public credit to foster the relatively highest rates of long-term growth and development in the economy as a whole.
A monopoly on the creation of public credit, as provided by Article I of the U.S. Federal Constitution, and the focussing of that public credit to foster full employment in combined public and private enterprises most beneficial to the general interest in sustained technological progress, is the principal instrument through which the government fosters optimal rates of growth of income, output, and tax-revenue base, in the economy as a whole.
The general rule which ought to be applied, is that, in the physical economy as such, the state must foster relatively high rates of capital-intensity, power-intensity, and scientific and technological progress. This is achieved chiefly, by the use of tax-incentives and deployment of low-cost public credit, to favor the recycling of margins of relative “free energy” in economic output into technology-driver forms of productive and related investment.
In short, the problem of the interaction between the two axiomatically distinct kinds of processes, is almost entirely a matter of the responsibility, by governments of sovereign national economies, to regulate monetary and financial affairs. The object of such regulation must be to bring about and maintain the third of the three possible forms of interaction identified here.
|
Footnotes |
||
1. On the subject of the present writer’s use of the term “not-entropy.” It has been widely accepted classroom doctrine, for more than a century, that all inorganic processes tend to run down; this argument was posed by Britain’s Lord Kelvin, during the middle of the last century. On Kelvin’s instruction, his doctrine was given a mathematical form by two German academics, Rudolf Clausius and Hermann Grassman, who employed their own kinematic model of heat-exchange, in an imaginary, confined, particular gas-system, as a purported explanation of French scientist Sadi Carnot’s caloric theory of heat. Kelvin and his collaborators defined the “frictional” loss of extractable work in such a mechanical model of a thermodynamical system, as “entropy.” This was Kelvin’s Second Law of Thermodynamics. During the 1940’s, the Massachusetts Institute of Technology’s Prof. Norbert Wiener employed the term “negative entropy” (shortened to the neologism “negentropy”) to signify the statistical form of “reversed entropy,” in the sense of a famous reconstruction of the Clausius-Grassman model by Ludwig Boltzmann: Boltzmann’s so-called H-theorem. Wiener’s argument was employed to found what has become known as “information theory.” In this connection, Wiener claimed that the H-theorem provided a statistical means for measuring the “information content” of not only coded electronic transmissions, but also human communication of ideas. Earlier usage had identified “negative entropy” as a characteristic of the apparent violation of Kelvin’s so-called “Second Law” by living processes in general, as distinct from the ostensibly entropic characteristics of ordinary non-living phenomena. For several decades, beginning 1948, this writer insisted that only the first meaning of “negentropy,” as typified by the commonly characteristic distinction of living processes, should be accepted usage. Recently, for practical reasons, he has substituted the term “not-entropy.”
2. Norbert Wiener, Cybernetics, or Control and Communication in the Animal and the Machine (New York: John Wiley, 1948). As of 1948, there existed two principal, previously developed premises in this writer’s knowledge, for his competence to assault Wiener’s thesis. During the late 1930’s, this writer, already a dedicated follower of Gottfried Leibniz, had been deeply involved in constructing a proof of the absurdity of the arguments against Leibniz central to Immanuel Kant’s Critique of Pure Reason. In 1948, he recognized the crucial fallacies of Wiener’s “statistical information theory” to be a crude replication of the central argument, on the subject of the theory of knowledge, in Kant’s three famous Critiques. Secondly, by 1946-47, the writer’s interest had become absorbed with his own somewhat critical view of the use of the notion of “negative entropy” in biology, as, for example, by LeComte du Nouy.
3. Lyndon H. LaRouche, Jr., So, You Wish To Learn All About Economics? (New York: New Benjamin Franklin House, 1984), passim. “Relative” in “potential relative population-density” signifies, simply, the differences in quality of man-developed, and man-depleted habitat referenced.
4. Georg Cantor, Beiträge zur Begründung der transfiniten Mengenlehre, in Georg Cantors Gesammelte Abhandlungen mathematischen und philosophischen Inhalts, ed. by Ernst Zermelo (1932) (Berlin: Verlag Julius Springer, 1990), pp. 282-356 [hereinafter, “Abhandlungen”]. The standard English translation of this work, by the Franco-English critic of Cantor, Philip E.B. Jourdain, is published as Georg Cantor, Contributions to the Founding of the Theory of Transfinite Numbers (New York: Dover Publications, 1955). The publisher’s note for the current reprint edition implies, erroneously, that Dover first published this in 1956. The author’s original copy of the Dover reprint of the Jourdain translation (still in the writer’s possession) was purchased, in a Minneapolis, Minnesota bookstore, in 1952. Caution is suggested in reading Jourdain’s Preface and lengthy Introduction to this translation; in real life, that translator was not quite the faithful collaborator of Cantor which he pretends to have been.
5. Or, one might say, relative cardinality or power.
6. As a result of the control of the Berlin Academy of Science by the Newton devotee Frederick II of Prussia, and the subsequent, post-1814 takeover of France’s Ecole Polytechnique by the Newtonians Laplace and Cauchy, the geometric method of Plato, Cusa, Leonardo da Vinci, Kepler, and Leibniz tended to be supplanted by the method of algebraic infinite series. Most significant was Leonhard Euler’s attack upon Leibniz, on the issue of infinite algebraic series: Euler’s denial of the existence of absolute mathematical discontinuities. The political success of the Newtonians, over the course of the Nineteenth century, in establishing Euler’s infinite series for natural logarithms as a standard of mathematical proof, led into the positivism of the Russell-Whitehead Principia Mathematica, and the, related, wild-eyed extremism of present-day “chaos theory.” Thus, Karl Weierstrass and his former pupil, Georg Cantor, while attacking the same general problem of mathematics as Riemann, the existence of discontinuities, engaged the Newtonian adversary on his own terrain, infinite series, whereas Riemann attacked the problem from the standpoint of geometry: hence, Riemann’s notably greater success for physics.
7. Although this writer consistently referenced this debt to Riemann during his one-semester course taught at various campuses during the 1966-73 interval, the first published use of the term “LaRouche-Riemann” method originated in November 1978, when the term was adopted for the purposes of a joint forecasting venture undertaken by the Executive Intelligence Review, in cooperation with the Fusion Energy Foundation. At that time, the prompting consideration was the fact that isentropic compression in thermonuclear fusion, as predefined mathematically by Riemann’s 1859 Über die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite, has mathematical analogies to the propagation of the “shock-wave”-like phase-shifts generated through technological revolutions. (See Riemann, Werke, cited in footnote 8 below, pp. 157-175.) As a by-product of this same, highly successful, forecasting project, a translation of the Riemann paper was prepared by the same task-force; this appeared in The International Journal of Fusion Energy, Vol. 2, No. 3, 1980, pp. 1-23, under the title, “On the Propagation of Plane Airwaves of Finite Amplitude.” This emphasis on Riemann’s “shock-wave” paper, reflected an ongoing, friendly quarrel of the period, between the writer’s organization and Lawrence Livermore Laboratories, on the mathematics of thermonuclear ignition in inertial confinement. Notably, that conflict reflected the influence of the U.S. Army Air Corps’ Anglophile science adviser, Theodore von Karman, in promoting Lord Rayleigh’s fanatical incompetency against Riemann’s method. On the success of the 1979-83 EIR Quarterly Economic Forecasts, see David P. Goldman, “Volcker Caught in Mammoth Fraud,” Executive Intelligence Review, Vol. 10, No. 42, Nov. 1, 1983.
8. Bernhard Riemann, “Über die Hypothesen, welche der Geometrie zu Grunde liegen (On the Hypotheses Which Underlie Geometry),” in Bernhard Riemanns gesammelte mathematische Werke [hereinafter referenced as “Riemann, Werke”], ed. by Heinrich Weber (New York: Dover Publications [reprint], 1953), pp. 272-287. [For a passable English translation of the text, see the Henry S. White translation in David Eugene Smith, A Source Book in Mathematics (New York: Dover Publications, 1959), pp. 411-425.] Those concerned with the formal-mathematical implications of the dissertation as such, are referred to the later (1858) Paris representation of this: “Commentatio mathematica, qua respondere tenatur questionii ab IIIma Academia Parisiensi propositae,” in Werke, pp. 391-404 (Latin), with appended notes by Weber, pp. 405-423 (German).
9. “Es führt dies hinüber in das Gebiet einer andern Wissenschaft, in das Gebiet der Physik, welches wohl die Natur der heutigen Veranlassung nicht zu betreten erlaubt.” Loc. cit., p. 286.
10. Plato’s term for the set of axioms and postulates underlying a theorem-lattice is hypothesis.
11. Nicolaus of Cusa, De Docta Ignorantia (1440), passim [trans. by Jasper Hopkins as Nicholas of Cusa on Learned Ignorance (Minneapolis: Arthur M. Banning Press, 1995)].
12. Riemann, “II. Maßverhaeltnisse, deren eine Mannigfaltigkeit von n Dimensionen fähig ist ....,” op. cit., in Werke, pp. 276-283.
13. See Greek Mathematical Works, Vol. II, trans. by Ivor Thomas (Cambridge, Mass.: Harvard University Press, Loeb Classical Library, 1980), pp. 266-273. Cf., Lyndon H. LaRouche, Jr., “What Is God, That Man Is in His Image?,” Fidelio, Vol. IV, No. 1, Spring 1995, pp. 28-29.
14. Ibid.
15. Divide the domain of science as a whole among three topical areas, areas differentiated from one another by the limitations of man’s powers of sense-perception. Let what can be identified as a phenomenon, by the sense-perceptual apparatus, be named the domain of macrophysics. What is inaccessible in the very large (such as seeing directly the phenomenon of the distance between the Earth and the moon), belongs to the domain of astrophysics. Phenomena which occur on a scale too small for discrimination directly by our senses, are of the domain of microphysics. Thus, the most elementary physical ideas of astrophysics and microphysics belong entirely to the domain of Platonic ideas. It is the student’s practice of rigor in reliving the discoveries of Plato’s Academy at Athens, and of Archimedes, from the Fourth and Third centuries,B.C.E.which is the prerequisite training of the student’s powers of judgment, for addressing the domains of astrophysics and microphysics. More fundamental, is what might be set aside, for purposes of classroom discussion, as a fourth department of scientific events: causality. The senses could never show us the cause of even those events which sense-perception might adequately identify: Cause exists for knowledge only in the domain of Platonic ideas.
16. See C.F. Gauss Werke, Vol. IX (New York: Georg Olms Verlag, 1981), passim.
17. Riemann, Werke, p. 525.
18. Such an inconsistency does not prove, intrinsically, either that the proposition, or the mathematics is wrong. It forces us to conceptualize the idea of the existence of such an inconsistency.
19. In short, when a speaker employs the term “hypothesis” as a synonym for “conjectured,” or “intuited” solution to a riddle, for example, the speaker is showing himself to be illiterate in science. However, that sort of illiteracy does not identify the precise sense in which Isaac Newton misuses the same term; Newton’s argument is that of the radical philosophical empiricists in the tradition of Sarpi, Galileo, Hobbes, Descartes, et al.: Newton is asserting that he relies solely upon sense-certainty. Newton is insisting—however wrongly—that there are nothing but “natural ingredients” of sense-phenomena in his system.
20. Nicolaus of Cusa, op. cit., passim. Cusa reworked Archimedes’ theorems on quadrature of the circle, producing what he identified as a superior approach to Archimedes’ determination of π. This discovery was incorporated in De Docta Ignorantia (1440), but Cusa supplied a formal elaboration in his “On the Quadrature of the Circle” (1450) (trans. by William F. Wertz, Jr., Fidelio, Vol. III, No. 1, Spring 1994, pp. 56-63). The new principle of hypothesis, which Cusa develops on the basis of his proof that π is transcendental, is known as the isoperimetric principle: The Euclid axioms, that point and straight line are self-evident, are discarded, and replaced by that isoperimetric principle which, in first approximation, treats the existence of circular action as primary (e.g., “self-evident”).
21. See “20. John and Jacob Bernoulli, The Brachystochrone,” in A Source Book in Mathematics, 1200-1800, ed. by D.J. Struik (Princeton, N.J.: Princeton University Press, 1986), pp. 391-399.
22. Riemann, “Plan der Untersuchung,” op. cit., in Werke, pp. 272-273.
23. Despite the early influence of Ernst Mach’s positivism, Einstein repeatedly showed himself a moral, as well as most capable scientist. His acknowledgement of the debt to Bernhard Riemann’s habilitation dissertation, as to Johannes Kepler, like his later collaboration with Kurt Gödel, typifies this. There is a consistent quality to these expressions of his morality in science; Einstein’s expression of disgust with the fraudulent physics adopted by the 1920’s Solvay Conferences, “God does not play dice,” illustrates this. This morality centers around a consistent commitment to the rule of the universe by some efficient principle of Reason, in the sense that Plato, Nicolaus of Cusa, Kepler, Leibniz, Gauss, and Riemann are committed to that principle of science. However, as in his qualified defense of Max Planck, against the savagery of Mach’s fanatically positivist devotees, he halts at the point the issue demands a thorough-going repudiation of the essential assumptions of empiricism.
24. See discussion of Sarpi and his followers, in Lyndon H. LaRouche, Jr., “Why Most Nobel Prize Economists Are Quacks,” Executive Intelligence Review, Vol. 22, No. 30, July 28, 1995, passim.
25. Riemann, op. cit., in Werke, pp. 272-273: “Bekanntlich setzt die Geometrie sowohl den Begriff des Raumes, als die ersten Grundbegriffe für die Constructionen im Raume als etwas Gegebenes voraus. Sie giebt von ihnen nur Nominaldefinitionen, während die wesentlichen Bestimmungen in Form von Axiomen auftreten. Das Verhältniss dieser Voraussetzungen bleibt dabei im Dunkeln; man sieht weder ein, ob und wie weit ihre Verbindung nothwendig, noch a priori, ob sie möglich ist. Diese Dunkelheit wurde auch von Euklid bis Legendre, um den berühmtesten neueren Bearbeiter der Geometrie zu nennen, weder von Mathematikern, noch von den Philosophen, welche sich damit beschäftigten, gehoben.... Hiervon aber ist eine notwendige Folge, dass die Sätze der Geometrie sich nicht aus allgemeinen Grö[ESET]enbegriffen ableiten lassen, sondern dass diejenigen Eigenschaften, durch welche sich der Raum von anderen denkbaren dreifach ausgedehnten Größen unterscheidet, nur aus der Erfahrung entnommen werden können.”
26. Ibid., p. 286.
27. This issue was already stated, in their own terms, by Leibniz and Jean Bernoulli, in the 1690’s. Once Christiaan Huyghens learned, in 1677, that, during the previous year his former student, Ole Rømer, had given a measurement of approximately 3×108 meters per second for the “speed of light,” Huyghens recognized immediately the implications of a constant rate of retarded light propagation for reflection and refraction. [See Poul Rasmussen, “Ole Rømer and the Discovery of the Speed of Light,” 21st Century Science & Technology, Vol. 6, No. 1, Spring 1993. See also, Christiaan Huyghens, A Treatise on Light (1690) (New York: Dover Publications, 1962).] Leibniz’s attacks on the incompetence, for physics, of the algebraic method employed by Newton, and his understanding of the requirement of a “non-algebraic” (i.e., transcendental) method, instead, reflected most significantly the demonstration of principles of reflection and refraction of light consistent with a constant rate of retarded propagation which is independent of the notions possible in terms of a naive physical space-time.
28. Riemann, “I. Begriff einer nfach ausgedehnten Größe,” op. cit., in Werke, pp. 273-276.
29. C.F. Gauss, “Zur Theorie der biquadratischen Reste,” in C.F. Gauss Werke, op. cit., Vol. II, ed. by E. Schering, pp. 313-385, including notes by Shering.
30. J.F. Herbart was a famous opponent of the philosophy of Immanuel Kant. He came under the influence of Professor of History Friedrich Schiller at the Jena university, and became later a protégé of Wilhelm von Humboldt, assigned to Kant’s former university at Königsberg for a long period. During the middle of the 1830’s, Herbart was invited to C.F. Gauss’ Göttingen University, where he delivered a famous series of lectures. It was in this connection that Riemann was first exposed to him. Riemann’s critical references to some of Herbart’s arguments contain the material referenced at this point in his “Hypothesen”; see Riemann, “I. Zur Psychologie unter Metaphysik,” in Werke, pp. 509-520.
31. Riemann, “Ma[ESET]verhältnisse, deren ...,” op. cit., in Werke, p. 276.
32. “Es wird daher, um festen Boden zu gewinnen, zwar eine abstracte Untersuchung in Formeln nicht zu vermeiden sein, die Resultate derselben aber werden sich im geometrischen Gewande darstellen lassen.... [S]ind die Grundlagen enthalten in der berühmten Abhandlung des Herrn Geheimen Hofraths Gauss über die krummen Flächen.” Op. cit., in Werke, p. 276. Riemann is referencing one of the most famous, and influential discoveries by C.F. Gauss, made doubly famous by the problems of Special Relativity. Gauss’ summary work on this subject was originally published, in Latin, in 1828, under the title “Disquisitiones Generales Circa Superficies Curvas” (in C.F. Gauss Werke, op. cit, Vol. IV, pp. 217-258). However, it would be useful to read, also, Gauss’ “Theorie der krummen Flächen” (in ibid., Vol. VIII, pp. 363-452).
33. This was the issue of Newton devotee Leonhard Euler’s notorious 1761 attack upon Leibniz’s Monadology. See Lyndon H. LaRouche, Jr., “Appendix XI: Euler’s Fallacies on the Subjects of Infinite Divisibility and Leibniz’s Monads,” The Science of Christian Economy (Washington, D.C.: Schiller Institute, 1991), pp. 407-425.
34. Riemann was born on Sept. 17, 1826 (Werke, p. 541); the presentation of his habilitation dissertation occurred on June 10, 1854 (ibid., p. 272n).
35. If that fact were not made plain to students, and other “consumers” of economists’ work-product, the result would tend to be the type of superstition already typical of most Nobel-Prize-winning economists and their dupes. What we know is that for which we are able to account in terms of the manner in which we came to know it.
36. Georg Cantor, op. cit.
37. Georg Cantor, Grundlagen einer allgemeinen Mannigfaltigkeitslehre (Leipzig: 1883). Originally published as Über unendliche lineare Punktmannigfaltigkeiten, in Abhandlungen, op. cit., pp. 139-246.
38. See footnote 4.
39. E.g., “Mitteilungen zur Lehre vom Transfiniten,” in Abhandlungen, op. cit., pp. 378-440.
40. Riemann, in Werke, pp. 509-520. My colleague, Dr. Jonathan Tennenbaum, has pointed out C.F. Gauss’ devastating ridicule of Kant’s work. Cantor, in the “Mitteilungen,” expresses similar contempt for Kant.
41. Using the term “type” in Cantor’s sense.
42. It is not necessary to treat the subject of the Good in the present context. On that, see Lyndon H. LaRouche, Jr., “The Truth About Temporal Eternity,” Fidelio, Vol. III, No. 2, Summer 1994, passim.
43. Critique of Pure Reason (1781), Prolegomena to Any Future Metaphysic (1783), Critique of Practical Reason (1788), and Critique of Judgment (1790).
44. See Lyndon H. LaRouche, Jr., “Mozart’s 1782-1786 Revolution in Music,” Fidelio, Vol. I, No. 4, Winter 1992, and Bruce Director, “What Mathematics Can Learn From Classical Music,” Fidelio, Vol. III, No. 4, Winter 1994. The late Beethoven string quartets referenced are: E-flat major, Opus 127; B-flat major (The “Grosse Fuge” quartet), Opus 130; A-minor, Opus 132; B-flat major (“Grosse Fuge”), Opus 133; and, F major, Opus 135.
45. Felix Klein, Famous Problems of Elementary Geometry (1895), trans. by W.W. Beman and D.E. Smith, ed. by R.C. Archibald (New York: Chelsea Publishing Co., 1980), pp. 49-80. Klein is probably aware that the proof that π is transcendental, was first given, from the standpoint of geometry, by Nicolaus of Cusa; he knows, without question, that the transcendental character of π was conclusively established by Leibniz et al., during the 1690’s. Yet, he insists that the transcendence of π was first proven by F. Lindemann, in 1882! The reason for Klein’s gentle fraud, is that he is defending Euler’s attack on Leibniz in the matter of “infinite series.” Thus, Klein is motivated by his insistence upon an Euler-based algebraic “proof” (and, no other!) even at the expense of perpetrating a monstrous fraud on the history of science.
46. See, for example, The Political Economy of the American Revolution, ed. by Nancy Spannaus and Christopher White (New York: Campaigner Publications, 1977).
47. In the U.S.A.’s Federal constitutional tradition, the regional authority lies primarily with the Federal state, except as national interest may prescribe a Federal responsibility.
48. National water-management, including principal ports and inland waterways, watersheds, and relevant sanitation are included. Also, general public transportation should be either a governmental economic responsibility, or government-regulated area of private investment. The organization and regulation of adequate national power-supplies, adequately provided for the regions and localities, is a key governmental responsibility. Basic urban infrastructure is also a governmental responsibility, chiefly of local government under national guidance and state regulation as to standards.
|
Relations of Measure Applicable From So, You Wish To Learn All About Economics?, by Lyndon H. LaRouche, Jr. Excerpted from So, You Wish to Learn All About Economics?: A Text on Elementary Mathematical Economics (New York: New Benjamin Franklin House, 1984), pp. 73-76. For a further summary statement of the issues, see the author’s “On the Subject of God,” Fidelio, Vol. II, No .1, Spring, 1993, sections on “Physical Economy” and “Demography,” pp. 24-28. See the Appendix, p. XX, for an application of the LaRouche-Riemann method to today’s U.S. economy. Since we are measuring increase of potential relative population-density, we must begin with population. Since the unit of reproduction of the population is the household, we measure population first as a census of households, and count persons as members of households. We then define the labor force in terms of households, as labor-force members of households, as the labor force “produced” by households. We define the labor force by means of analysis of the demographic composition of households. We analyze the population of the household first by age interval, and secondly by economic function. Broadly, we assort the household population among three primary age groupings: (1) below modal age for entry into the labor force; (2) modal age range of the labor force; and (3) above modal age range of the labor force. We subdivide the first among infants, children under six years of age, pre-adolescents, and adolescents. We subdivide the second primary age grouping approximately in decade-long age ranges. We subdivide the third primary age grouping by five-year age ranges (preferably, for actuarial reasons). We divide the second primary group into two functional categories: household and labor-force, obtaining an estmate such as “65% of the labor-force age range are members of the labor force.” We assort all households into two primary categories of function, according to the primary labor-force function of that household. The fact that two members of the same household may fall into different functional categories of labor-force employment, or that a person may shift from one to the other functional category is irrelevant, since it is change in the relative magnitudes of the two functional categories which is more significant for us than the small margin of statistical error incurred by choosing one good, consistent accounting procedure for ambiguous instances. This primary functional assortment of households is between the operatives and overhead expense categories of modal employment of associated labor-force members of those households. At this point our emphasis shifts to the operatives’ component of the total labor force. All calculations performed are based on 100% of this segment of the total labor force. The operatives’ segment is divided between agricultural production, as broadly defined (fishing, forestry, etc.), and industrial production broadly defined (manufacturing, construction, mining, transportation, energy production and distribution, communications, and operatives otherwise employed in maintenance of basic economic infrastructure). The analysis of production begins with the distinction between the two market-baskets and the two subcategories of each’s final commodities. The flow of production is traced backwards through intermediate products and raw materials to natural resources. This analysis of production flows is cross-compared with the following analysis of production of physical-goods output as a whole: 100% of the operatives’ component of the labor foce is compared with 100% of the physical-goods output of the society (economy). This 100% of physical-goods output is analyzed as follows. Symbol V: The portion of total physical-goods output required by households of 100% of the operatives’ segment. Energy of the system. Symbol C: Capital goods consumed by production of physical goods, including costs of basic economic infrastructure of physical-goods production. This includes plant and machinery, maintenance of basic economic infrastructure, and a materials-in-progress inventory at the level required to maintain utilization of capacity. This includes only that portion of capital-goods output required as Energy of the System. Symbol S: Gross Operating Profit (of the consolidated agro-industrial enterprise). [T [= total physical-goods output] - (C + V) = S. Symbol D: Total Overhead Expense. This includes consumer goods (of households associated with overhead expense categories of employment of the labor force), plus capital-goods consumed by categories of overhead expense. Energy of the System. Symbol S′: Net Operating Profit margin of physical-goods output. (S-D) = S′. Free Energy. If we reduce Overhead Expense (D) to a properly constructed economic-functional chart of accounts, there are elements of Services which must tend to increase with either increase of levels of physical goods output or increase of productive powers of labor. For example: a function subsuming the notions of both level of technology in practice and rate of advancement of such technology, specifies a required minimal level of culture of the labor force, which, in turn, subsumes educational requirements. Scientific and technical services to production and to maintenance of the productive powers of labor of members of households, are instances of the varieties of the accounting budgeter’s Semi-Variable Expenses which have a clear functional relationship in magnitude to the maintenance and increase of the productive powers of labor. Large portions of Overhead Expense as a whole have no attributable functional determination of this sort; in a “post-industrial society” drift, the majority of all Overhead Expense allotments should not have been tolerated at all, or should have been savagely reduced in relative amount. For this reason, we must employ the parameter S′/(C + V), rather than S′/(C +V+D), as the correlative of the ratio of free energy of the system. For purposes of National Income Accounting, we employ: Symbol S/(C + V): Productivity (As distinct from “productive powers of labor”). Symbol D/(C + V): Expense Ratio. Symbol C/V: Capital-Intensity. Symbol S′/(C + V): Rate of Profit. These ratios require the conditions:
|
|||
What is the Schiller Institute?
Fidelio Table of Contents from 1992-1996
Fidelio Table of Contents from 1997-2001
Fidelio Table of Contents from 2002-present
Beautiful Front Covers of Fidelio Magazine

Join the Schiller Institute,
and help make a new, golden Renaissance!
MOST BACK ISSUES ARE STILL AVAILABLE! One hundred pages in each issue, of groundbreaking original research on philosophy, history, music, classical culture, news, translations, and reviews. Individual copies, while they last, are $5.00 each plus shipping
Subscribe to Fidelio:
Only $20 for 4 issues, $40 for 8 issues.
Overseas subscriptions: $40 for 4 issues.
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Home | Search | About | Fidelio | Economy | Strategy | Justice | Conferences | Join
Highlights | Calendar | Music | Books | Concerts | Links | Education | Health
What's New | LaRouche | Spanish Pages | Poetry | Maps |
Dialogue of Cultures
© Copyright Schiller Institute, Inc. 2006 All Rights Reserved.

