

|
||
|
The Essential Role of
‘Time-Reversal’ in Mathematical Economics by Lyndon H. LaRouche, Jr. |
||
 |
||
|
‘When’ is the future? At what point in time?...
The answer to this seeming paradox, was already known by Plato, by Augustine of Hippo, and therefore, also, Thomas Aquinas: All time is subsumed under a general regine of simultaneity! |
||
For related articles, scroll down or click here.
The Essential Role of ‘Time-Reversal’ in Mathematical Economics
by Lyndon H. LaRouche, Jr.
October 3, 1996
| This article originally appeared in Executive Intelligence Review, Oct. 11, 1996 (Vol. 23, No. 41). |
In order to make clear the apparent paradox, I asked the audience to acknowledge the perplexity, the which this notion of “time-reversal” would pose to the ordinary professional mathematician. I state here, as then: How might one represent, mathematically, a function in which an event in the future might serve as the apparent cause for an event in the present? This was, in fact, being considered by the famous Soviet physicist Sakharov, as a formal problem in mathematical physics, during the later years of his life.4 The issue of the functional role of “time-reversal,” is the most important of the fundamental issues confronting mathematical physics today. It is also a key, axiomatic issue in the field of natural law, and, in a related way, important for cleansing theology of certain cultish, intrinsically pagan superstitions, which have no proper place in the teaching of Christianity, Judaism, and Islam. Here, all those issues are implicit; but, it is the decisive role of “time-reversal” in any competent economics teaching, which is the topic explicitly addressed in the following pages.
This physical principle of “time-reversal,” and its importance, were themes which had been featured aspects of my original discoveries in physical economy, during the 1948-1952 interval. For example, some of my former students will recall, that I had stressed that central, “world-line” feature of physical-economic processes in my lectures delivered at Columbia University campus, during the Spring 1973 semester. I had stressed that, in the published version of my lectures on the dialectical examination of Karl Marx’s economics.5 During preceding years, I had written and lectured often on related principles underlying the Classical method of composition and performance of motivic-thorough-composition in music,6 and had addressed this recently, in response to remarks, on the subject of “time-reversal,” by Nobel Prize economist Kenneth Arrow.7
Nonetheless, although the notion of time-reversal has always been the core of my discoveries and teaching in the science of physical economy, it is only since the Reston address, that I have received demands, from among my collaborators, for in-depth background expositions on these, and interrelated matters. One might speculate, that, perhaps, it is the psychological tremors set off by the onrushing, global disintegration of the world’s monetary and financial systems, which increase sensible people’s interest in questions of physical-economic fundamentals. My students had often heard this conception presented by me earlier. The difference is, this time, they had decided it was now necessary to consider actually mastering the concept, rather than simply acknowledging the importance which I place upon it. Thus, at last, the stunning implications of the relevant paradox have been noticed.
The Future As Change
A dog reaches for a bone; a dog hunts for prey not yet seen, heard, or smelled. How does human reaction to the idea of the future, differ from what an observer might attribute to the “intentions” controlling the dog’s action? In short, the difference is, that, except when a man is behaving with the simple-mindedness of a macho, materialist, or empiricist, the object of the relevant expression of human intent, is not the apprehension of a sensory object, but, rather, a desired change in the axiomatic characteristics of some referenced pattern of human behavior. That point may be stated otherwise: What is desired is not a mere event, nor a mere change in opinion, but, rather, either a change in hypothesis, or theorem.
The change which distinguishes characteristically human ideas of the future, from the bestial intent which might be expressed by a beast, or in a man’s moment of beastliness, is always of the ontological quality designated by the connotations of the term Platonic idea, rather than mere contemplation of a real, or merely desired object of sense-perception.8
We may desire the coming into being of a condition which is consistent with a theorem of an established hypothesis, a condition which does not presently exist. More profoundly, we may desire a revolutionary change, a new hypothesis, to replace the reigning hypothesis of existing practice. The properties of Plato’s method of hypothesis, are indispensable keys for rendering transparent the meaning of the “time-reversal” paradox. Bernhard Riemann’s 1854 habilitation dissertation9 then serves as a pivotal reference, for transforming the mathematics of “time-reversal” into the form of expression suited to validation according to Nicolaus of Cusa’s and Riemann’s principle of experimental physics: measurement.10
Let us now restate the case in the terms of my customary pedagogical tactic, from the standpoint of a system of theorem-lattices.
For pedagogical purposes, define a deductive “theorem-lattice” as follows. Given, any set of propositions, for which it may be shown, that no pairwise permutation is, apparently, deductively inconsistent. Employing Plato’s Socratic method, adduce a set of axioms, postulates, and definitions, the which must necessarily underlie that set of propositions. The latter then represents the hypothesis for that set of propositions, and the propositions qualify as theorems. In this case, there also exists an empty or non-empty set of additional propositions, the which could qualify as possible theorems of the set defined by that hypothesis. The addition of the qualifiable theorems from the latter set, to the initial set of propositions, defines a deductive theorem-lattice of that hypothesis.
Any deductive mathematics for which extension is presumed, arbitrarily, to be perfectly continuous,11 qualifies as such a deductive theorem-lattice. Thus, for pedagogical purposes of first approximation, any series of events which might be stated as consistent propositions of a presently generally accepted classroom mathematics, can be supplied a formal representation in the terms of a theorem-lattice, in the celebrated fashion of the time-worn Euclidean-geometry classroom. From such a mathematics, any consistent, commonplace schoolbook variety of lower undergraduate mathematical-physics is derived, such as the gas theory of Ludwig Boltzmann, and the crude, if sometimes complex systems of B. Russell devotees, such as Norbert Wiener’s pseudo-science of “information theory” and John V. Neumann’s theory of games.12
Although the principle of theorem-lattices upon which we are to focus, applies equally to all Classical forms of poetry, music, drama, and plastic art, we develop the relevant notions for mathematical physics and physical economy; the case for music is employed only to the degree wanted to illustrate features of physics, leaving to other locations the relevance of the same principle of rationality in art generally. We begin at a point which leads most directly to the fundamental discovery of principle set forth in Riemann’s 1854 habilitation dissertation: the celebrated measurement of the curvature of our planet Earth by Eratosthenes.13
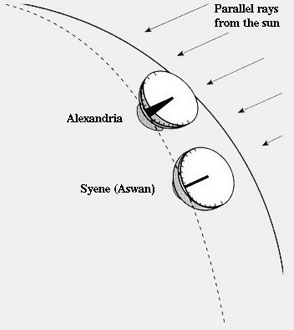
In recent time, I have often employed this discovery by Eratosthenes. That choice reflects the fact that this discovery provides the simplest, cleanest example of the way in which Platonic ideas arise in every fundamental, experimental discovery of physical principle. By comparing the angles cast by the noonday shadow upon the interior of hemispherical sundials, along the meridian linking Syene (Aswan) to Alexandria, in Egypt, Eratosthenes demonstrated, geodetically, that the Earth was a spheroid, estimating the Earth’s polar diameter with a margin of error of approximately fifty miles [See Figure 1]
.
| FIGURE 1. Eratosthenes’ method of measuring the size of the Earth.
Eratosthenes’ method (Third century B.C.E.) focussed on the difference, or anomaly, between the angles of shadows cast on two identical sundials at divergent latitudes. The significance of the experimental lies not in its extradordinaily accurate computation, but in its demonstration that knowledte, rather tham being based on experience, is actually based on discovering the contradictions implicit in our opinions about experience. In the illustration, two hemispherical sundials are placed on approximately a meridian circle at Alexandria and Syene (Aswan) in Egypt, at noon on the day of the summer solstice. The gnomon in the center of each sundial points straight to the center of the Earth. The gnomon casts no shadow at Syene, but a shadow of 7.2° at Alexandria. By knowing the idstance between the two cities (~490 miles), Eratosthenes was able to calculate the Earth’s circumference to be ~24,500 miles—which is accurate to within 50 miles.! |
 |
The relevant paradox is, that Eratosthenes measured the curvature of the Earth’s meridian more than two thousand years before any person was to have seen our planet’s curvature.14 The principle of the Earth’s curvature, as adduced thus, represents a Platonic idea: a conception of measurable relationship, a relationship which is not directly perceived as a sense-perception, nor as a new theorem of an existing deductive form of theorem-lattice.15
All such notions of measurable relationship which underlie the principles of astrophysics,16 are obtained only as “Platonic ideas.” From mankind’s successes in astrophysics, we derived later the method to open up the domain of microphysics.
In mathematics and mathematical physics, for example, a “Platonic idea” appears only as cognitive mental activity within the mind of either an original discoverer, or, of a student who comes to know that idea in the only way possible, through replicating the mental act of original discovery within the confines of the student’s own, sovereign mental processes. In both cases, original discoverer, or student, knowledge can not be obtained by mere classroom and textbook learning of the means to pass an examination, such as that idiot-savant’s delight, the multiple-choice questionnaire; it must be acquired by the kind of deductively-discontinuous mental processes unique to generating an original discovery. In the lesser case, the Platonic idea appears as the initial act of discovery of a theorem which is consistent with an implicitly preexisting hypothesis.17 In the higher-ranking case, the same method of original discovery is the means by which the discovery of new axioms (e.g., a superior hypothesis) is accomplished.
As Riemann introduces this notion in his 1854 habilitation dissertation18: The interdependent issues of hypothesis and of physical space-time curvature become unignorable in mathematical physics, whenever an experimental paradox compels us to introduce a validated new principle of experimental physics. The paradoxes so posed are identical in principle with the famous ontological paradox of Plato’s Parmenides dialogue.19 It is at this juncture, that the central role of “time-reversal” is implicitly posed to mathematical physics, and to economic science.
At this point, define this connection as of a type.20 Construct a preliminary definition of this type in its relatively most rudimentary terms. For this first-approximation definition, employ a pedagogical ruse borrowed from elementary Euclidean geometry. To the degree that the hypothesis underlying a deductive theorem-lattice is fixed, the lattice acquires the form of a deductive architecture, an architecture whose construction determines a sequence, or chains of sequences. In Classical motivic thorough-composition, or Motivführung,21 the notion of sequence inheres in the nature of music: The unit of musical composition, is the interval, not the individual tone. In Classical composition, as distinct from musical composition more generally, the unit of thought is the polyphonic elaboration of a modal pair of intervals. The quality of sequence is paradigmatic for all naive (e.g., reductionist) notions of functional time in mathematical physics generally: a sequence of occurrences, such as a sequence of propositions, or theorems.
What transpires within the underlying hypothesis, during the lapse of time the lattice’s petals bloom? The hypothesis itself remains unchanged during all moments of the unfolding. So, in the case of any chains of events, the which are presumably defined by propositions of a deductive theorem-lattice, the hypothesis underlying that lattice does not change with any referenced place in mathematical space-time. To employ a relevant Biblical allusion: The hypothesis is the “alpha and omega” of the array of theorems which it underlies.22
The Science of Musical Composition
Consider the challenge of performing a Classical thorough-composed musical work by Mozart, Beethoven, Brahms, et al. The point most relevant for attention here, is that since Mozart’s derivation of the principle of works such as his six Haydn quartets, his K.475 Fantasy, etc., from a study of J.S. Bach’s A Musical Offering, each masterwork by a Classical composer,23 from Mozart through Brahms, is based upon an implicitly transparent, but not deductive, succession of modalities. The effect is, that the composition has the form of a succession of modal hypotheses, such that the concluding resolution of the composition defines the composition as a whole as an expression of the principle of higher hypothesis.24 Thus, the characteristic of any successful such application of this method of composition, is the following:
The organization of the process of composition, for such a case, is of the following form:
1. Each phase of the composition is of a quasi-mathematical type, representable by an underlying hypothesis, designated by the general, Riemannian form hi (i = 0, 1, 2, ... , i, ... , m).25
h0,h1,h2,h3,...hm.
Thus, the compositional process is representable by a series of the form:
2. Thus, according to Plato’s solutions for the ontological paradox posed in his Parmenides, the process of change underlying that deductively discontinuous series h i, is of the relative type known as an “higher hypothesis,” H j, also symbolized as:
(hi)j
(j = 1, 2, 3, ..., j, ..., n).26
3. But, higher hypothesis Hj is a member of a series “hypothesizing the higher hypothesis.” In this example, that “hypothesizing the higher hypothesis” defines the domain of all Classical motivic thorough-composition. Thus, the general representation of the domain, is symbolized for our reference here as:
(Hj)k
or,
[(hi)j]k.
4. These functions are each and all representable as a sequence of events: polyphonic intervals, is the elementary character of the immediate event within performed music; the ordering of hypotheses (e.g., modalities), is also presented in sequence; etc.
5. However, every hypothesis, or higher hypothesizing, acts simultaneously upon every possible element of sequence within the domain which that hypothesis underlies.27 Thus, all times within the historical past and future are subsumed by:
[(hi)j]k.
6. The characteristic action within that domain of change, is symbolized by:
[hi + 1)/(hi](k, K+q)
n employed by Mozart, Beethoven, Schubert, Schumann, Brahms, et al., is that which Mozart derived from mastering the implications of the six-voice “Ricercare” from Bach’s A Musical Offering. The Beethoven Opus 13, like the Opus 111, like the Mozart Ave Verum Corpus, is an example of the same method (i.e., higher hypothesis) of ordering of successive modalities, the which one had met in earlier applications of this Bach-rooted discovery, such as Mozart’s six Haydn quartets and the K.475 keyboard Fantasy. Mozart’s derivation of the role of the Lydian mode in the works such as that Ave Verum Corpus, or the significance of that mode in Beethoven’s Opus 132, are expressions of the hereditary pervasiveness of that principle of musical higher hypothesis, the which Wolfgang Mozart adduced from this study of Bach’s A Musical Offering.
Two additional facts must be stressed here, by aid of this reference to the musical case.
First, a relevant observation on the role of differentiated higher hypotheses. Each successful piece composed according to that principle of thorough-composition, represents a series of mutually distinct hypotheses (modalities). The unity of the composition as a whole, lies, therefore, in that corresponding principle of higher hypothesis, which subsumes (underlies) the resolutions connecting the succession of hypotheses (modalities) of which that piece is composed. Thus, in the relevant, Leibnizian analysis situs, the generalized principle of motivic thorough-composition, the which Mozart adduced from his study of Bach’s A Musical Offering, is of the order of hypothesizing the higher hypothesis. E.g.:
[(hi)j]k.
Second, the role of higher hypothesis, of hypothesizing the higher hypothesis, has the same significance in music as Leibniz’s principle of necessary and sufficient reason in mathematical physics. At this juncture, consider, once more, the author’s frequently supplied illustration of the relevant point.
There are principally two diametrically opposing views on the subject of the nature of mathematical physics: one, the semi-literate, relatively more popular, misconception, that mathematical physics is the discovery of an explanation for a physical phenomenon, from the repertoire of a fixed, hypothesis-free type of generally accepted classroom mathematics; second, the view, shared by Leibniz and Riemann, for example, that crucial discoveries of physical principle, generated, outside of mathematics, in the domain of experimental physics, oblige us to overturn previously existing mathematical physics, to fit the axiomatic features of mathematics to the discovered principles of nature. This issue was sharply defined during the 1690’s, as the uncompromisable issues of principled difference, between the algebraic school of Galileo, Descartes, Newton, et al., and the non-algebraic, or transcendental school of Leibniz, Jean Bernouilli, et al., and, just over a century and a half later, Riemann. This was the core of the underlying difference in hypothesis, between the fraudulent, and unworkable calculus of Newton, and the previously introduced, and successful calculus of Leibniz.28
For all but those who were blinded to facts by their fanatical devotion to the cults of René Descartes and Isaac Newton, the case for Leibniz and Bernouilli’s argument, was established conclusively by Bernouilli’s and Leibniz’s collaboration in recognizing the identity of two apparently distinct experimental-physical discoveries of principle, during the late Seventeenth century: Christiaan Huyghens’ study of the experimental-physical principle of isochronism in the gravitational field,29 and the work by Huyghens’ student Ole Rømer and Huyghens on the implications of Rømer’s astrophysical measurement of the speed of light.30
The implication of this 1690’s discovery of a principle of special relativity, by Bernouilli, Leibniz, et al., is that the notion of mechanistic “causality,” which is characteristic of all such philosophical reductionists as the materialists, empiricists, and logical positivists, cannot account for the actual measurements of action within real physical space-time. The interdependency between the two Seventeenth-century discoveries had discredited entirely the mechanistic, “pull-me/push-me” world of Galileo, Hobbes, Descartes, Locke, Hooke, and Newton. It also discredited, in advance, the same mechanistic world-outlook and method of David Hume, Adam Smith, and Leonhard Euler. Today, that discredited, but still widely advocated view, is no better than bad “science fiction.” It is an Ockhamite delusion, a mere “virtual reality.”31
Modern empiricism, prior to the 1690’s, relied upon an algebraic method derived from an Ockhamite reading of formal Euclidean geometry.32 It relied upon the arbitrary, axiomatic presumption, that space-time was extended without limit in four mutually independent senses of direction (“dimensions”), and that this extension, of space-time itself, was perfectly continuous, without possibility of interruption (of “discontinuity”). This four-dimensional space-time manifold served the empiricists as a kind of empty box, into which a continuous fluid of some sort (an “ether”) might be poured by a Newton, or J. Clerk Maxwell, or not; “ether,” or no “ether,” physics was degraded into algebraic descriptions of the movement of perceptible (or, merely imagined) bodies in terms of that box-like four-dimensional manifold.
During the 1690’s of Leibniz and Bernouilli, that algebraic view was challenged in a crucial way, by the measurable demonstration of isochronicity in a gravitational field. The measurement of a speed of propagation of light, was another devastating refutation of the algebraic world-outlook. The combined effect of Jean Bernouilli’s experimental design: the measurable coherence between isochronism in the gravitational field, and the same form of function respecting refraction of radiation propagated at a measurable speed, was devastating refutation of the empiricist’s algebraic standpoint in method [See Figures 2(a)-(d)].
The type of paradox posed by this experimental evidence was the same which had been confronted, and resolved by Eratosthenes, in his approximate measurement of the curvature of the Earth’s surface. In this case, the existence of a general curvature of physical space-time, inconsistent with the empiricist’s algebraic method, was the import of the measurement.
Specifically, to bring axiomatic assumptions of mathematics into conformity with the experimental evidence, it was necessary to eradicate the notions of limitless and perfectly continuous extension of space-time, and to introduce certain additional reforms, those placed in view by Riemann’s referenced, 1854 dissertation.
In Riemann’s Platonic, Leibnizian physics, every discovered principle of nature which is validated by the methods of experimental-physical measurement specified by Cusa,33 functions, like spatial extension and time, as an extensible dimension of a general physical-space-time manifold. With each validated addition of such a dimensionality, we are obliged to validate, by experimental measurement, not only the reality of the individual principle considered as if in isolation, but also the “geodetic curvature” of the physical space-time so defined. The demonstrated phenomenon of isochronicity in the gravitational field, and a measurable rate of retarded propagation of electromagnetic radiation, are individual principles which demand that we discover, that we measure, whether or not this principle is associated with some change in the curvature of the physical space-time associated with such a manifold. It is not sufficient to show that a finite “speed of light” exists; it is also necessary to show, how this affects the measurable curvature of the physical space-time manifold: in other words, to practice a “non-Euclidean” geometry.
The point of reference, from Eratosthenes’ experimental estimate of the Earth’s curvature, through Riemann’s habilitation dissertation, and beyond, the standpoint for comparison of a Euclidean with a so-called “non-Euclidean” manifold, is the so-called “Pythagorean”:
√ (x2 + y2 + z2) .
Given: an n-fold, Riemannian, physical-space-time manifold. What is the difference in the distance between two points in that manifold, when compared with the Pythagorean metric of Euclidean space-time?
The first step of approximation, in introducing this notion to the secondary pupil, is to challenge the student knowledgeable in solid Euclidean geometry and spherical trigonometry, to show how a person living on a very large, spherically curved surface would be able, by means of geodesy, not only to show that that is indeed such a surface, but to measure the curvature of that surface. We would challenge the student to define the kinds of mathematical methods and procedures required to conduct the relevant experimental measurements. With that grounding, the student is on the road to understanding how and why Riemann, in composing his habilitation dissertation, relied upon the referenced earlier work of Gauss.
Look at Leibniz’s notion of necessary and sufficient reason from this vantage-point. Apply the same conceptions to Mindy Pechenuk’s August 31, 1996 presentation of the succession of hypotheses of which Mozart’s Ave Verum Corpus is composed.
Turn around Riemann’s notion of the physical space-time manifold. Given: a measurement, in quasi-Pythagorean terms, of the estimated characteristic curvature of a physical-space-time manifold. What is the hypothesis which corresponds to this measurement? The hypothesis which meets those requirements, is a demonstration of Leibniz’s principle of necessary and sufficient reason. Given: any crucial type of event; that is to say, an event which is typical of the measurement of the characteristic quasi-Pythagorean of the real manifold in question. The hypothesis which determines that physical space-time manifold, to have that typical curvature, expresses necessary and sufficient reason.
In physical economy, as in Mozart’s Ave Verum Corpus, it is the Riemannian form of representation of a physical space-time manifold, which supplies us the most characteristic representation of the relevant “curvature.” For reasons which need not be a topic of separate elaboration at this moment, each added “dimension” of a well-ordered Riemann series of the Leibniz analysis situs form
[(n + 1)/n],
appears in the form of a validated formal discontinuity in the previously established form of mathematical physics (for example). It is the increase of density of such discontinuities, for any arbitrarily selected choice of interval of action, which measures the relevant, relative cardinality of the characteristic interval of action of two such Riemannian manifolds. In physical economy, as in the developmental processes of Mozart’s Ave Verum Corpus, it is this type of increase of cardinality, the which is the strictest measurement of the characteristic difference of two compared manifolds. This choice of characteristic is in correspondence with the general expression already given:
[(hi)j]k.
In this sense of the matter, there is a relevant, direct correlation, among: (1) the “cardinality” of typical action within a physical space-time; (2) the order of the Riemannian manifold, which, according to Leibniz’s principle of necessary and sufficient reason, represents that physical space-time; and, (3) the implicitly adducible hypothesis underlying statements expressed in terms of that manifold. It is the correlation of some physical value with the notion of the relative cardinality of the characteristic of action for a given manifold, which is the basis for a physical science, such as physical economy, and for Classical motivic thorough-composition.34
What Does ‘Linear’ Mean?
In the Ockhamite and related forms of algebraic methods, derived from a formalist interpretation of Euclidean geometry, the characteristic unit of action within algebraic space-time is a quantity of linear extension. Thus, the “distance” between two points is measured, typically, by the simplest form of the “Pythagorean”:
√ (x2 + y2 + z2) ..
In “non-Euclidean physical geometries,” such as that of Riemann’s habilitation dissertation, the unit of displacement (“distance”) on a curved surface, has an outward appearance which would have been tolerated by Leonhard Euler, et al.; but, underlying that mere appearance, the smallest length of displacement “outwardly” represented by a simple line or arc, is transfinitely dense with “holes,” called “discontinuities,” sometimes identified by, and sometimes arbitrarily suppressed as, the infinitesimals inhering in the Leibniz calculus.35 These are each transinfinitesimally small interruptions, which mark the location of an actual, or possible new singularity, such as a new “dimension” of an expanded Riemannian manifold.36
In other words, we must distinguish between the mere appearance of a simply linear displacement, and the physically efficient content masked by that displacement, the density of discontinuities/singularities. We must distinguish, thus, between the formalist’s merely virtual reality, and that which the formalist masks, the underlying, physical reality.
These considerations lead to conclusions which will prove indispensable, at a later point here, in tackling crucial implications of functional “time-reversal” in physical-economic and other processes.
Consider a significantly simplified representative of a relatively simple experiment, an illustration nonetheless accurate enough for the point being made. Construct a cycloid by rolling a circle along the underside of a line. As for C. Huyghens’ case,37 the attributed, radiated impulse of gravity is normal to the line on which the circle has been rolled. Designate the low point of the generated cycloid by O, and mark a point, A, other than O, on the descending pathway of cycloid [See Figure 3]. Construct the straight line AO. As for the Huyghens experimental study of isochronicity,38 compare the lapsed time required for two balls to fall to the lowest point O, from A, one along the constrained pathway defined by the arc, the other the inclined straight line. Observe that the longer pathway, the arc, is faster. Then, observe that the lapsed time to fall to O, along the arc, from any other point B, is the same as from A: isochronicity.39
In those Riemannian manifolds which experimental physics imposes upon us, two leading considerations are immediately relevant to examining that algebraic fallacy, of assumed linearity, upon which the mathematical physics of Sarpi, Galileo, Descartes, Newton, Euler, Cauchy, Clausius, Helmholtz, et al., are each and all premised.
First: Any change in an axiomatic assumption, imposed upon us by validated discovery of a revolutionary principle from the domain of experimental physics, establishes a new hypothesis, which supersedes, and is inconsistent with every preceding hypothesis. Each of the two hypotheses, new and old, compared, represents a different manifold, and physical space-time curvature, different from, and functionally inconsistent with the other.
Nonetheless, although no theorem in either of these two theorem-lattices will be consistent with any theorem in the other, the valid experimental physics of the old lattice, is carried forward within the new theorems internal to the new theorem-lattice. In this case, the relatively valid theorem-results in the old lattice, have the form of the relatively degenerate case, in respect to the new lattice. Therefore, the mathematical function containing the transition from phenomena satisfactorily explained by the old hypothesis, to the experimental phenomena characteristic of the new, will be typified by the relevant discontinuity40 in the function constructed to describe such a case.41
Second: For any valid function, the transfinite cardinality of action is, primarily, the density of discontinuities determined by the cumulative “dimensions” of the relevant physical space-time manifold. This “property” is crucial for identifying the expression of “time-reversal” within the action of, for example, performing a composition which were composed as an application of Classical motivic thorough-composition: conductor Furtwängler’s “playing between the notes.”
As Riemann stresses in his Hypothesen dissertation, the root of the difference in curvature expressed, by two mutually distinct physical-space-time manifolds, lies within the contrasted hypotheses. To borrow the argot of the modern mathematics classroom, the differences in curvature express the “hereditary” impact of the differences in axiomatics, as these axiomatics are located within the respective, underlying hypotheses. One must sense the efficient immediacy of the correlation between a shading of difference in axioms, and a shading of difference in characteristic curvature of the associated manifold.
“Curvature” has been examined, since Eratosthenes, from the geodetic standpoint employed by C.F. Gauss, both in astrophysics and, in turn, in the revolutionary development of modern geodetic surveys. Even in those outwardly “innocent” excursions, the idea of curvature, generalized through the successive work of G. Monge, A.-M. Legendre, C. Gauss, Karl Jacobi, Jacob Steiner, et al., acquired new meaning through the discoveries of B. Riemann, and this in a way which is absent from the related work of such geometers as (the younger) Bolyai, and N. Lobachevski.42
In the common classroom and campus cant on the subject of “non-Euclidean geometry,” there is a tendency to seize, with wild-eyed zeal, on the matter of the “parallel postulate.” Such ivory-tower contemplation, has contributed much to the proliferation of tiresome, sterile, and utterly counterproductive academic sophistries on the subject. The viable issue often hidden under the cloak of “non-Euclidean geometry,” is not a matter of mathematical formalism; it is, as Riemann stresses throughout, a matter of experimental physics. As Riemann also stresses from the outset of the Hypothesen dissertation, the problem to be solved requires that we abandon the domain of deductive mathematical formalism, and look at the way in which physical reality demonstrates the pervasive fallacy of the generally accepted classroom view of the Euclidean axiomatic system as a whole.43
The crucial evidence is directly contrary to those modern mathematical physicists who insist upon the presumption, that physical space-time in the small is either linear, or a nearly asymptotic approximation of blissful linearity. The truth of the matter is precisely the opposite: The smaller the interval of action, the more radically non-linear the microphysical domain becomes! Paradoxically, because of “time-reversal” considerations, as we shall show at a later point, here, the smaller the interval, the more pronounced the impact of the density of singularities, relative to the interval of action chosen.44
Riemann’s mathematical physics requires us to deny primary efficiency to the attributed linear span of displacement, and locate efficiency in the transfinite terms, of density of discontinuities (singularities) per interval of action. However, to render Riemann’s earth-shaking discovery transparent, we must leave the campus department of mathematical physics, for the laboratory of physical economy. We have now set the stage for the argument to be made. Now, we proceed to demystify “time-reversal” from that standpoint.

FOOTNOTES
1. Labor Day Weekend Conference, co-hosted by the Schiller Institute, Reston, Virgina, U.S.A., August 31-September 1, 1996.
2. A presentation by Mindy Pechenuk, with chorus directed by John Sigerson, during the second panel, August 31, 1996. This highly sophisticated, compact, and beautiful work, is among the most convenient illustrations of the same principle of “time-reversal” otherwise underlying both experimental physics in general, and physical-economic processes specifically. Any master’s Classical composition according to the principles of motivic thorough-composition, such as those of Wolfgang Mozart, L. v. Beethoven, F. Schubert, R. Schumann, Johannes Brahms, et al., must be performed by applying the developed conception reached at the close of the composition, to the interpretation of every portion of the composition, from the beginning of the performance of the composition. The modification so imposed by the intent of such a composer, results in what the celebrated conductor Wilhelm Furtwängler identified as “playing between the notes.” The relationship of the counterpoint in this motet to Mozart’s derivation of the principle of motivic composition from Bach’s A Musical Offering, illustrates the relevant historical point, that although full-composition motivic thorough-composition was introduced by Wolfgang Mozart during 1782-1783, as prompted by the preceding work of Joseph Haydn, motivic thorough-composition would not have been possible without the preceding development of the principles of counterpoint, based upon C=256, by Johann Sebastian Bach, whose work provided the basis for Mozart’s discoveries. Video recordings of the August 31 pedagogical presentation of the motet are available through the Schiller Institute.
3. As indicated in Lyndon H. LaRouche, Jr., “Leibniz From Riemann’s Standpoint,” Fidelio, Vol. V, No. 3, Fall 1996: notes 15, 18-20, pp. 21-22. (G.F.) Bernhard Riemann, Über die Hypothesen, welche der Geometrie zu Grunde liegen [“On The Hypotheses Which Underlie Geometry”: 1854 habilitation dissertation], in Bernhard Riemanns Gesammelte Mathematische Werke, ed. by H. Weber [reprint of (Stuttgart: B.G. Teubner, 1902)] (New York: Dover Publications, 1953) [also (Vaduz, Liechtenstein: Saendig Reprint Verlag], pp. 272-287. The specialist should supplement the habilitation dissertation with several additional Riemann and Gauss references. These include Riemann’s own later (Paris) report on the substance of his mathematical discussion in the 1854 habilitation proceedings. The most essential such references are, the following. For the reader of Latin: Commentatio mathematica, qua respondere tenatur quaestionii ab Illma Academia Parisiensi propositae, op. cit., pp. 391-404; the mathematics can be followed, with help of cross-reference to the appended notes, in German, pp. 405-423. On Riemann’s reference to Gauss on the relationship of biquadratic residues to a general theory of curved surfaces, see Carl Friedrich Gauss Werke [Werke] (Hildesheim: Georg Olms Verlag). Riemann references explicitly Theoria Residuorum Biquadraticorum: Commentatio Secunda (1831) (Werke, Vol. II, pp. 93-138); but see the German notice: Zur Theorie der Biquadratischen Reste (Werke, Vol. II, pp. 315-385). The text of Riemann’s dissertation references Disquisitiones Generales Circa Superficies Curvas (1828) (Werke, Vol. IV, pp. 217-258). But, for relevant background, see Gauss’ Allgemeine Auflösung der Aufgabe die Theile einer gegabenen Fläche so abzubilden Dass die Abbildeten in den Kleinsten Theilen ähnlich wird [“Copenhagen Prize Essay”] (1822) (Werke, Vol. IV, pp. 189-216). Compare with Riemann’s Theorie der Abel’schen Functionen (1857) (Riemann Werke, pp. 86-144), especially the celebrated Lehrsätze aus der analysis situs für die Theorie der Integrale von zweigliedrigen vollständigen Differentialen, pp. 96-99. The origins of Gauss’ development of biquadratic residues, are found in his 1799 doctoral dissertation, Disquisitiones Arithmeticae (1801) (Werke, Vol. I); it was the development of the early work of his doctoral dissertation, through later work in astrophysics and geodesy, which produced, twenty to thirty years later than the Disquisitiones, the refined notions of a general theory of curved surfaces, to which Riemann makes reference.
4. Andrei D. Sakharov, “Cosmological Models of the Universe with Reversal of Time’s Arrow,” in Collected Scientific Works (New York: Marcel Dekker, 1982), pp. 131-136 (originally published in ZhETF, 79:689-693 (1980) [trans. Sov. Phys. JETP, 52:349-351 (1980)]. See also, in the Collected Works: “Violation of CP Invariance, C Asymmetry, and Baryon Asymmetry of the Universe,” pp. 85-88; “The Baryonic Asymmetry of the Universe,” pp. 115-130; and “Maximum Temperature of Thermal Radiation,” pp. 137-150.
5. On “world line,” as presented in the Columbia University lectures, see Lyn Marcus (pen-name of Lyndon H. LaRouche, Jr.), Dialectical Economics (Lexington, Mass.: D.C. Heath, 1975), pps. 61-62, 134. The crux of my criticism of Karl Marx’s Capital, now as then, was to point to Marx’s repeated admission, that he had constructed his doctrine without considering the implications of technological progress; thus, what was generally accepted as “Marxist economics” among its professionally qualified scholars, was a parody of those combined, mechanistic doctrines of Quesnay, Adam Smith, et al., which each and all presumed zero-technological growth as the axiomatic basis underlying all of the fundamental theorems of the doctrine. I.e., they implicitly deny the distinction, the individual potential for creative mentation, which sets mankind apart from and above all the beasts, and which, thus, defines the only admissible basis for either an economic science or the study of history. An incident from the late 1950’s is relevant. An acquaintance invited me to deliver a lecture to a class of his students of Karl Marx’s Capital, Vol. III. When I identified the need to apply the implications of technological progress to correct the flawed notion of “extended reproduction” used by Marx, consternation erupted among both students and host!
6. Lyndon H. LaRouche, Jr., “That Which Underlies Motivic Thorough-Composition,” Executive Intelligence Review, Sept. 1, 1995 (Vol. 22, No. 35). _______, “Norbert Brainin on Motivführung,” Executive Intelligence Review, Sept. 22, 1995 (Vol. 22, No. 38) (also Fidelio, Vol. IV, No. 4, Winter 1995).
7. Lyndon H. LaRouche, Jr., “More ‘Nobel Lies,’ ” Executive Intelligence Review, May 31, 1996 (Vol. 23, No. 23).
8. For both Riemann and the present writer, this notion of the “ontological” quality of a “Platonic idea” references the ontological paradox underlying Plato’s Parmenides dialogue. The notion is, that the type of paradox elaborated within the Parmenides can be solved only by recognizing change, rather than “fixed objects” of sense-perception, as the form of the primary substance within physical space-time. I.e., in this dialogue, which serves as an implied preface for all of his later dialogues, Plato reconstructs Heracleitus’ much-cited, and often misapprehended statement: Nothing is constant, but change. Cf. Proclus’ Commentary on Plato’s Parmenides, trans. by Glenn R. Morrow and John M. Dillon (Princeton, N.J.: Princeton University Press, 1987).
9. Op. cit.
10. See Nicolaus of Cusa, On Learned Ignorance (De Docta Ignorantia), trans. by Jasper Hopkins (Minneapolis: Banning Press, 1985). See also, B. Riemann, habilitation dissertation, passim, respecting the axiomatic distinction between mathematical physics and experimental physics.
11. E.g., not only the mathematics of Galileo, Descartes, and Newton, but also all mathematics and mathematical physics derived from the widely popularized, tautological hoax concocted by Leonhard Euler in his “Letters to a German Princess” (1761) [Letters of Euler on Different Subjects in Natural Philosophy, Addressed to a German Princess, ed. by David Brewster (New York: Harper & Brothers, 1840)]. Euler’s hoax was his fraudulent claim, to have proven the pervasively perfect continuity of extension in physical space-time, by means of a formal geometry (“virtual reality”), in which perfectly continuous extension is axiomatically preassumed. This is the same hoax from which celebrated followers of Euler, such as Lambert, Lagrange, Laplace, Cauchy, Hermite, Lindemann, Felix Klein, B. Russell, et al., derived their insistence upon a universe consistent with nothing but perfectly continuous functions (e.g., “the sliding rule,” infinite algebraic series). Notably, in the mathematical physics of G. Leibniz or B. Riemann, Euler’s tautological fallacy is rejected. This rejection is the precondition for non-paralogical solutions for true “non-linear” functions.
12. Both Wiener and, later, V. Neumann were more than merely students of Bertrand Russell, they were epigonoi of Russell’s beastly doctrines: Russell’s wildly radical positivism in mathematics and views on physical science, and in that ultra-fascistic streak of utopianism characteristic of Russell, H.G. Wells, and their own and Aleister Crowley’s acolytes: Aldous and Julian Huxley, and George Orwell. The beastly and mechanistic “theory of the mind” which is axiomatic to Wiener’s “information theory” and V. Neumann’s “systems analysis,” pervades every aspect of the putative scientific work, as well as social and psychological doctrines of them all.
13. Lyndon H. LaRouche, Jr., “Leibniz From Riemann’s Standpoint,” op. cit., pp. 25-27, including Figure 1. In a modern case, Christiaan Huyghens’ discovery of isochronism in the gravitational field, already took physics beyond the comprehension of Descartes’ and related mathematics. The demonstration, through the work of Ole Rømer, Huyghens, and Jean Bernouilli, that a finite rate of retarded propagation of light, coincided with gravitational isochronism, already demanded a non-Euclidean geometry of relativistic physics.
14. The still-ocean “horizon effect” does not meet the requirement of experimental physics: clear measurement of relationship. Cf. the relevance of Leonardo da Vinci’s treatment of a vanishing-point as a property of vision, rather than objects.
15. So, although we may see the moon as a distant object, the measurable relationship governing the distance between the moon and Earth is not an object of simple sense-perception. Consider the work of Thales, Aristarchus, and Eratosthenes on this subject, as an example of the problem.
16. As will be emphasized below, the notions of relationship employed here go beyond the generally accepted limits of conceptions found in the mathematical-physics classroom, into the broader range specified for analysis situs by G. Leibniz. The notion of experimental-physical relationship stressed in this report, is the efficient relations among events, propositions, theorem-lattices, and the hierarchy of hypothesis. This is introduced in the illustrative treatment of motivic thorough-composition, below.
17. Not all pre-existing hypotheses are consciously established. One’s opinion-making may be regulated by underlying axiomatic assumptions of whose efficient existence one is not aware, assumptions which have the characteristic of irrational “blind faith.” Thus, the corresponding hypothesis exists, but the victim is unaware of its existence as an hypothesis. Thus, most of today’s secondary and university students of mathematical subject-matters, would accept Isaac Newton’s fraudulent hypotheses non fingo, because they are ignorant of the hypothetical nature of those axiomatic assumptions, the which are responsible for their acceptance of Newton’s wild claims on sundry matters. [See, e.g., Riemann Werke, op. cit., p. 525.] Thus, to state the general case, one must reference “pre-existing,” rather than merely “established” hypothesis.
18. Op. cit.
19. Lyndon H. LaRouche, Jr., “Leibniz From Riemann’s Standpoint,” op. cit. See pp. 18-24, under the sub-heading, “Riemann’s Principle of Hypothesis.”
20. In first approximation, this implies Georg Cantor’s notion of a mathematical type.
21. This is the term for motivic thorough-composition attributed to Joseph Haydn, as employed by former Primarius of the Amadeus Quartet, Norbert Brainin. See my “Norbert Brainin on Motivführung,” op. cit.
22. Thus, the higher hypothesis is the “alpha and omega” of the array of hypothesis which it underlies; hypothesizing the higher hypothesis, is the “alpha and omega” of the array of higher hypotheses which it underlies; and, Plato’s Good underlies, similarly, every past, present, and future change which exists within the universe.
23. This does not apply to Romantic composers, such as Franz Liszt, Hector Berlioz, Richard Wagner, et al., nor to the so-called “moderns.” The essence of such styles of musical composition, is that they are premised upon the argument laid down by Immanuel Kant’s Critique of Judgment, that there is no discernible rational principle in composition of works of art.
24. The Ave Verum Corpus was selected as a beautiful, short work, which demonstrates this principle of motivic thorough-composition. It is the role of the mental functions associated with the principle of higher hypothesis, which underlies the distinction between legitimate use of the term “musical genius,” as contrasted with the lack of such insight in the mind of the learned musical pedant, or Romantic. This is key to the meaning of Furtwängler’s famous references to “playing between the notes”: see more on this, below.
25. I.e., n, n+1, n+2, .... In other words, these successive modalities must have the form of effect of physical space-time curvatures of increasing mathematical cardinality (increase of implicitly denumerable density of singularities per interval of action).
26. It should be sufficient at this point, merely to note the fact that the notion of functional relationship indicated by these formulations falls under the implied category of Leibniz’s generalized notion of analysis situs.
27. As Mindy Pechenuk emphasizes in her August 31, 1996 presentation of the Mozart Ave Verum Corpus, the mind of the performer must recognize, functionally, not only every quoted mode of each passage, but, also, all of those modalities are defined implicitly by reversing (mentally) the direction (e.g., up, or down) of the succession of intervals considered, both in the same voice, and also with respect to cross-voice, polyphonic intervals. Thus, the theorem-lattice of any modality, or succession of modalities, employed within a composition, includes all of these additional “possibilities,” whether they are explicitly quoted, or not. That general scope of the relevant theorem- and hypotheses-lattices, subsumed under the general functional relationship symbolized above, applies throughout the domain of all possible Classical forms of motivic thorough-composition.
28. I.e., putting to one side Newton devotée Augustin Cauchy’s Euleresque “correction” of Leibniz.
29. Christiaan Huyghens, The Pendulum Clock, trans. by Richard J, Blackwell (Ames, Iowa: Iowa State University Press, 1986).
30. Christiaan Huygens, Treatise on Light (1678), trans. by S.P. Thompson (New York: Dover Publications, 1962). See also Poul Rasmussen, “Ole Rømer and the Discovery of The Speed of Light,” 21st Century Science and Technology, Vol. 6, No. 1, Spring 1993; and “Johann and Jakob Bernoulli. The Brachystochrone,” in A Source Book in Mathematics, 1200-1800, ed. by Dirk J. Struik (Princeton, N.J.: Princeton University Press, 1986); pp. 391-399 [Note the French/German alternates for the brothers Jean/Johann and Jacques/Jakob of this illustrious, multi-generational extended family of Swiss mathematicians. Recent texts have standardized the spelling of the family surname as “Bernoulli.”—Ed.]
31. “Okhamite” (var. “Occamite”): Followers of William of Ockham’s radically reductionist parody of Aristotle. Approximately a century and a half after the establishment of a modern European science based upon Nicolaus of Cusa’s principle of experimental-physical measurement (A.C.E. 1441), Ockham admirer Paolo Sarpi, and his followers Galileo Galilei, Francis Bacon, et al., introduced the mechanistic doctrine of empiricism, in the effort to destroy the established modern science of Cusa, Luca Pacioli, Leonardo da Vinci, Johannes Kepler, et al. Leibniz, the French Leibniz school of Gaspard Monge, Lazare Carnot, et al., Gauss, and Riemann typify the continuation of modern science, despite the relative political hegemony of the empiricism and positivism of Laplace, Cauchy, Kelvin, Clausius, Helmholtz, Mach, et al.
32. For our purposes here, there is no significant distinction to be made among such forms of linear, mechanistic reductionism as materialism, empiricism, and positivism. With the convergence of the two Cartesian schools, of British Nineteenth-century philosophical radicalism, and the positivism of such fanatical Newtonians as Laplace, Cauchy, Helmholtz, et al., the accidental, earlier distinctions between the Cartesians and British empiricists were dissolved, as if asymptotically, into a neo-Kantian homogeneity.
33. Nicolaus of Cusa, De Docta Ignorantia, op. cit.
34. For example: In the case of any masterwork in the mode of the type of motivic thorough-composition introduced by W. Mozart, the cardinality expressed measures the creative mental power applied by the composer, and, hopefully, exciting the performance.
35. In abstraction, a “purely” linear displacement (without “holes”) may be generalized as a displacement whose density of discontinuities is “0.”
36. The use of the terms “transfinite” and “transinfinitesimal,” here, should be recognized as involving, not only the distinction between the mathematical transfinite of Georg Cantor, and bad notions of “infinite” and “infinitesimal,” but also the distinction, implicit in the discoveries of B. Riemann, between a merely mathematical (formal) transfinite, and an ontological (physically efficient) transfinite.
37. The Pendulum Clock, op. cit.
38. Ibid.
39. Ibid.
40. I.e., “transinfinitesimal.”
41. For an example of this, see B. Riemann, Über die Fortpflanzung ebener Luftwellen von endlicher Schwingungsweite (“On the Propagation of Plane Air Waves of Finite Amplitude”: otherwise known as Riemann’s exposition on the cohering topics of sonic shock waves, transsonic flight, and isentropic compression), Riemann Werke [see note 3, above], pp. 157-175. Note that Riemann was not the original discoverer of sonic “booms”; that distinction belongs to Leonardo da Vinci, who also recognized the finite speed of propagation of sound, through such means as observing lightning-strokes.
42. On relevant exchanges between C. Gauss and the members of the Bolyai family, see Carl Friedrich Gauss: Der “Fürst der Mathematiker”, Briefen und Gesprächen, ed. by Kurt-R. Biermann (Munich: Verlag C.H. Beck, 1990). On Gauss’ relations to the younger Bolyai and the work of Lobachevski, see pps. 27, 137, 139-140, 176. Editor Biermann (p. 27) cites Gauss’ remarks to Wolfgang Bolyai, Johann’s father, as found in Briefwechsel zwischen Carl Friedrich Gauss und Wolfgang Bolyai, ed. by Franz Schmidt and Paul Staeckel (Leipzig: 1899): “Hingegen mußte sich der Sohn seines Jugendfreundes Bolyai, Janos [Johann] Bolyai, ebenfalls einer der Pioniere der nichteuklidische Geometrie, mit der merkwürdigen Annerkennung bescheiden, Gauss könne ihn nicht loben, denn ihn loben heisse, sich selbst zu loben.” (Gauss could not praise Janos’ discovery, if to praise him, would mean that Gauss were praising himself.) Cf. Biermann, op. cit., p. 139. On Gauss on Lobachevski, see Gauss’ November 28, 1846 letter to H.C. Schumacher, in Carl Friedrich Gauss: H.C. Schumacher Briefwechsel, Vol. III (Hildesheim: Georg Olms Verlag, 1975), pp. 246-247.
43. The referenced case of L. Euler’s tautological hoax, is a useful choice of example of such formalist traditions of academics’ propensities for being most pedantically arrogant, when they are at their tiresomely tedious worst on such accounts. They reason like “jailhouse lawyers,” imposing upon a selective interpretation of the language of a chance-read precedent, the delusion that the application of deductive casuistry to a mere quibble, must command the mighty rivers of the judiciary to bend to the proponent’s exalted sense of cabalistic authority. Pathetic? Then, Leonhard Euler was more pathetic than such a petty jailhouse quibbler, and Lambert, Lagrange, Laplace, Cauchy, Clausius, Helmholtz, Maxwell, Hermite, Lindemann, and F. Klein, among many others, after him. Construct a deductive proof, which rests entirely on the mere arbitrary presumption, that extension in space-time, is essentially linear, unbounded, and perfectly continuous; then, employ that systemic error of axiomatic presumption, pervasively, to construct a deductive edifice, whose relevant conclusion is: “Extension in space-time is perfectly linear, boundless, and perfectly continuous, Q.E.D.” Only a fool or a charlatan would propose to prove, or disprove an axiom of the system by means of a chain of deduction from the theorem-lattice which depends upon that axiom. On this premise of this pathetic, deductive, fallacy of composition, today’s generally accepted mathematics classroom is politically ideologized to the proverbial gills, with the pagan religious cult-dogma of Euler’s deluded view of infinite algebraic series: “linearization in the very small.”
44. 21st Century Science & Technology quarterly, will soon publish a report by Laurence Hecht, documenting those fundamental discoveries in electrodynamics which empiricists, such as J. Clerk Maxwell and H. Helmholtz, worked to ban from the classroom and textbook (21st Century Science & Technology, Vol. 9, No. 3, Fall 1996). Hecht’s report is the outcome of what had been, initially, the 1975 prompting of me and my associates by the University of Chicago’s Professor Robert Moon, deceased during late 1989. It was Moon who first emphasized the deeper significance of the discoveries of the founder of electrodynamics, the Monge Ecole Polytechnique’s A.M. Ampère. The implications of Ampère’s work were rescued from oblivion by C. Gauss’ and B. Riemann’s collaborator Wilhelm Weber. However, the circles of Britain’s Lord Kelvin, including the practiced scientific hoaxster Hermann Helmholtz, and J. Clerk Maxwell, were dedicated to destroy the influence of Gauss, Weber, and Riemann; Maxwell apologized for his unacknowledged parodying of the electrodynamics discoveries of the Gauss-Weber-Riemann circle, by emphasizing, that it was the intent of the British circles to refuse “to acknowledge any geometries but our own [Newtonian dogma].” During the middle of the Nineteenth century, Weber demonstrated the relationship between “strong” and “weak” forces, on the scale of atomic and nuclear physics, and, then, estimated coefficients, derived from experimental inquiry, which are close to Twentieth-century values. The role of “strong forces” within the domain of the microphysical small, continues to defy efficiently those among today’s fanatics who continue to insist on a mathematical physics which presumes linearity, or near-linearity in the very small. Hecht’s report presents the relevant accomplishments of W. Weber, aided by Gauss, in developing experimental proof for the relevant discovery of nuclear “strong forces,” as being implicit in the discovery of Ampère.
![]()
schiller@schillerinstitute.org
The Schiller Institute
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Thank you for supporting the Schiller Institute. Your membership and contributions enable us to publish FIDELIO Magazine, and to sponsor concerts, conferences, and other activities which represent critical interventions into the policy making and cultural life of the nation and the world.
Contributions and memberships are not tax-deductible.
VISIT THESE OTHER PAGES:
Home | Search | About | Fidelio | Economy | Strategy | The LaRouche Frameup | Conferences
Links | LaRouche | Music | Join | Books | Concerts | Highlights | Education |
Health | Spanish Pages | Poetry | Dialogue of Cultures
Maps | What's New
© Copyright Schiller Institute, Inc. 2006. All Rights Reserved.

