
| Reviewing An Original Discovery | ||
|
Believing Is Not
Necessarily Knowing by Lyndon H. LaRouche, Jr. Part I |
||
 |
||
| EIRNS Pedagogical demonstrations by the LaRouche Youth Movement. Clockwise from left, cadre school presentations in Washington, D.C., California, California, and Boston, MA. |
For related articles, scroll down or click here.
Reviewing an Original Discovery
Believing Is Not Necessarily Knowing
by Lyndon H. LaRouche, Jr.
December 16, 2002
A see-saw battle between opposing forces of Classical science and philosophical reductionism, has reigned throughout globally extended ancient, medieval , and modern European civilization, up throught the present day.
Now, once again, a new youth movemnent has appeared an indispensable ingredient for the effort to rescue civilization; but, this time, let us build it more wisely, on the basis of lessons which should have been learned from the outcomes of the campaigns of the past. We must rapidly develop many veritable ‘platoons’ of truly qualified young intellectual leaders steeped in a distillation of the most crucial products of the Classical tradition to date. For this, we require not only a movement of education, but a political movement which is education in and of itself.
The root of the increasingly catastrophic failure of U.S. education policy of practice, over the recent thirty-odd years, may be summed up in five points of a general indictment:1
- Sense perception is not necessarily knowing.
- Learning is not necessarily knowing.
- Generally accepted opinion, academic or other, is not a standard for the definition of truth.
- Today’s teachers have not necessarily intended to educate or test their students in a manner suited to human beings.
- The radically reductionist fad known as “Information Theory,” as associated with the influence of Bertrand Russell devotees Norbert Wiener and John v. Neumann, was always a hoax. Thus, the educational methods adapted to the “information theory” hoax, such as the related so-called “new math,” are also a hoax.
That five-fold corruption is largely a product of a moral degeneration of our society which was embedded in those standards of general education and culture which were introduced, in pilot-phases, during the course of the 1945-1964 interval.2 During the middle to later 1960’s, this already emerging trend was unleashed with great destructive force, in forms such as the “rock-drug-sex youth-counterculture,” and the moral and economic decadence resulting from the intention to transform a formerly productive society into a “post-industrial” form of “consumer society” utopia. As a result of this post-Missiles Crisis cultural paradigm-shift, which descended upon the adolescents of the 1960’s, the world is now gripped, not only by the present, potentially terminal, systemic decline of the economies of Europe and the Americas, but by an ominous intellectual decadence among the generation presently occupying many leading positions, both in government and relevant private institutions.
Thus, we, most notably in the Americas and Europe, must recognize our nations as presently in the grip of that culturally induced 1964-2002 paradigm-shift in institutionalized popular opinion. This change has now reached the point of crisis at which the existence of this body of popular opinion almost assures us that today’s Europe and the Americas would not avoid an early collapse into what would become a prolonged new dark age for most of humanity. The practical means to avoid such an almost certain catastrophe are available, but the currently prevalent popular culture, combined with its corrupting impact on present educational institutions, would stubbornly resist any of those available, beneficial changes by means of which the economies and their nations might survive.
Therefore, the survival of civilization now depends upon the success of those among us who take the lead in rejecting, and seeking to overturn, very soon, that pathetic body of still currently prevalent popular opinion.
The presently developing international youth movement, whose specific qualities are referenced by this report, is a crucial factor in that effort for reeducation.
Relevant lessons from history show that sudden changes in prevalent, practiced culture, for better, or for worse, often occur through aid of the catalytic impact of youth movements. A youth movement gave birth to the transition from medieval, to modern European civilization, through the Italy-centered Fifteenth-century Renaissance. So, a youth movement centered around Lessing and Mendelssohn, the German Classic, was a crucial, trans-Atlantic factor in the Franklin-led American Revolution. Yet, an anti-Classical youth movement directed from London by the British Foreign Office’s Jeremy Bentham, played a crucial role in giving France the horrors of the Jacobin Terror and Napoleonic fascism. So, the introduction of the 1960’s “rock-drug-sex youth-counterculture,” was an essential contributing factor in transforming the previously successful form of U.S. economy axiomatically, from a successful producer society (albeit with serious flaws), into a decadent, parasitical, and self-doomed form of “consumer society.” The included result of the latter turn, is what has since become the self-inflicted terminal phase of material and moral collapse of a systemically failed world economy of today.
Look back, across the expanse of European history since Thales and Pythagoras, but especially since “Golden” Athens’ tragic folly in launching the Peloponnesian War. One ominous fact stands out.
We see there, in that history, repeatedly, an appalling fact. The renaissances of the past depended upon an intrinsically vulnerable, relative handful of apostles. In each renaissance, the continuation of that upturn was subsequently aborted, more or less, by its enemies. The enemies of progress were able, repeatedly, to mobilize those ruling forces of ignorant popular opinion, from the top-most ranks of society downwards, which misshaped the popular will, and thus induced the foolish majority of the people themselves to destroy or isolate the few worthwhile intellectual leaders available.
So, the legacies of murdered Presidents Abraham Lincoln and Franklin Roosevelt, and murdered Rev. Martin Luther King, have been virtually abandoned, or even explicitly betrayed by so many among their survivors. Thus, the despicable Democratic Party of Athens rallied popular opinion to murder Socrates judicially, and thus, ultimately, bring Athens’ self-inflicted ruin upon itself.
In history, the leaders with the sublime quality of a Socrates or France’s Jeanne d’Arc, are too few. This is not to recommend, perversely, the intrinsically evil Norman or Spanish inquisitions as a grim yardstick for measuring their heroic victims’ achievements. Let us be grateful for those handfuls of exceptional individuals, who led every renaissance; but, let us also be warned, that the impulse for progress has been repeatedly turned back, as it was by the 1966-1972 Nixon campaign’s “Southern Strategy.”
Remember, that Nixon’s “Southern Strategy” was a triumph of a combination of two passionately, morally illiterate, populist rabbles. This rabble included, on the one side, the neo-Confederate Nashville Agrarians’ obvious followers; on the other side, the corrosive role of the leadership of the so-called “rock-drug-sex youth-counterculture” of Ford Foundation-backed and other anti-Classical university campus rebels of the middle 1960’s. In effect, those ostensibly mutually opposing forces combined in converging effect, to unleash a process of moral decay of the campus-centered youth, which continued through the sans-culottes-like “Rainbow Coalition” of 1972 and beyond. It was those combined varieties of existentialists, including the “speech code” Jacobin Terror of the nation’s campuses and public schoolrooms, which have played a crucial part in transforming public and higher education of the U.S.A. and the Americas, especially the U.S.A., into the putrid mess it has become today.
In the history of European civilization since the period of Rome’s Second Punic War, the continuing cultural conflict within globally extended European civilization, has been, chiefly, the struggle of that decadent Roman legacy known genetically as Romanticism, in its recurring efforts to exterminate that Classical movement for truth which is associated, chiefly, with the Christian tradition of Plato.3
Among the numerous exemplary cases of this history, is the destruction of the Classical movement associated with Germany’s Abraham Kästner, Gotthold Lessing, Moses Mendelssohn, and Friedrich Schiller, by the succession of those waves of reactionary Romanticism expressed in such assorted forms as France’s Jacobin Terror, the rise of fascism under Napoleon Bonaparte, the waves of Romanticism spread in Germany following Napoleon’s victory at Jena-Auerstädt, and the increasing influence and depravity of Europe during the decades immediately following the Metternich-Castlereagh Vienna Congress and the Metternichean Carlsbad decrees. The fascist doctrine of the Napoleonic model of the state, as elaborated for Germany by G.W.F. Hegel, and the rise of Romanticism in poetry and the musical school of Czerny, Liszt, Berlioz, and Richard Wagner, are typical of the cases under which a great upward movement of the Greek Classical tradition has been, once again, aborted for a time by the mobbish thuggery of a Romantic resurgence.4
So, in the history of modern science, when Johannes Kepler, the Classical voice of the Golden Renaissance, had liberated astronomy from the Romantic folly shared among Claudius Ptolemy, Copernicus, and Tycho Brahe,5 Venice’s Paolo Sarpi unleashed the Romantic follies of his servant Galileo, and his agents Sir Francis Bacon and Thomas Hobbes, to launch that orgy of Romanticist empiricism associated with Descartes, Locke, Mandeville; this empiricist romp was continued by that Voltaire-led pack of salons known as the Eighteenth-century “Enlightenment” of Venetian Abbot Antonio Conti and his followers.
So, a see-saw battle between the opposing forces of Classical science and philosophical reductionism, has reigned throughout globally extended ancient, medieval, and modern European civilization, up through the present day.
Now, once again, a new youth movement has appeared an indispensable ingredient for the effort to rescue civilization; but, this time, let us build it more wisely, on the basis of lessons which should have been learned from the outcomes of the campaigns of the past. We must aim at producing what might be described loosely as a factor of mass-leadership. We must rapidly develop many veritable “platoons” of truly qualified, young intellectual leaders steeped in a distillation of the most crucial products of the Classical tradition to date. For this, we require not only a movement for education, but a political movement which is education in and of itself. That must be a mass-oriented movement of future world leaders, which seeks to inspire the kind of leadership in institutions today, which those present youth will represent when they become the nations’ leaders of a decade or more ahead. It must be based on an inner core of educational programs, around which other elements of education are organized. That approach to education is implicitly represented in the unfolding of this report.
The Needed Principles of Education
In service of that strategic purpose, the alternative to the ugly actuality of today’s prevalent educational policy, may be summed up in the following headlined points. These points, and the following exposition of their basis, include a relevant, featured summary of that core of my discoveries in a science of physical economy, which is otherwise distributed among my published accounts from over more than three decades to date. The relevance of those discoveries of mine, to the issues of educational policy, will become clear in the course of the following pages.
On this account, it is not merely relevant, but, functionally speaking, of crucial importance, to point once more to my published record of more than three decades, as consistently the world’s most successful long-range economic forecaster. The extraordinary quality of this comparative success, reflects the characteristic intellectual backwardness, the lack of consideration for scientific principle, among those putative rivals of mine, who practice the statistical methods prevalent among both university economics departments and U.S. government forecasting agencies, still today.6 Although my knowledge of many of the following matters here has been improved considerably, again and again, during the course of work done over the recent half-century, all of my unique accomplishments as an economist, has been the fruit of principled conceptions already crystallized during 1953.7 Thus, the evidence of my exemplary successes over some decades to date, will serve now to enrich today’s student’s sources of insight into the broader implications, for education and other missions, of the Classical physical principles on which my exemplary successes as a long-range forecaster have depended.8
As I shall show, economic science, when defined in the way in which the exemplary success of my forecasting demonstrates, should be recognized as implicitly “the science of humanity.” Strong language? Admittedly. Exaggerated? Not in the slightest degree! As I shall show, and prove, at least implicitly, in the following pages, that claim is more than justified, especially in the setting of today’s awful, global and systemic economic debacle.
The principled issues introduced in the list of summaries given below, reflect the starting-point of my definition of physical economy. That definition is summed up in two arguments. First, that: Physical economy, and its reflection as political economy, is premised upon the specific quality of principled difference which sets the member of the human species absolutely apart from, and above all lower forms of life. Second, that: Political-economy did not exist in practice, until the birth of the modern sovereign nation-state during Europe’s Fifteenth-century Renaissance’s introduction of the notion of the supreme political authority of that General Welfare principle of natural law which Leibniz later identified as “life, liberty, and the pursuit of happiness.”9 The existence of any acceptable practice of political-economy depends upon the submission of government to the supreme authority of that scientifically defined universal principle of natural law.
That said, the indicated principles of educational reform addressed here, are, in summary, as follows.
- The “axiomatically” absolute difference between members of the human species and higher apes, is typified by that paradox of “The Cave” presented by Plato. The generation of what prove to be experimentally validated solutions for that type of paradox, called “hypotheses,” is the gateway to the discovery of what are called, interchangeably, “universal physical principles,” or, principles otherwise recognized as in the form of Platonic “ideas.” The body of this quality of “ideas” uniquely constitutes the core of actually knowable truth.
- For today’s secondary or university science classroom, or comparable setting, the most convenient choice of benchmark for introducing a proof of that notion of “truth” to students today, is Carl Gauss’s conclusive exposure of the axiomatically fatal, systemic error, respecting physical science, perpetrated by such leading Eighteenth-century “Enlightenment” figures Euler and Lagrange. That error was identified explicitly by Gauss, in Gauss’s original, 1799 (Latin) presentation of the fundamental theorem of algebra.10 This proof of that theorem, by Gauss, supplied a rigorous definition of the notion of “the complex domain.” It also supported and clarified Leibniz’s earlier, original discovery of both the catenary-keyed notion of a universal physical principle of least action, and Leibniz’s related, transcendental conception of natural logarithms.
- These proofs by Leibniz, Gauss, et al., although initially situated within the domain of the functional (“phase-spatial”) relationship of the human individual to man-altered nature, are also the key to defining a related, but distinct, second category of universal principles. This second category provides an historical conception of the efficient principle of human social relations, such as the principles of what is known as Classical artistic composition, as these modes of intellectual organization of cooperation in society, bear on the increase of our species’ power to exist and prosper in the universe.
- The latter, properly adduced social principles of strictly Classical artistic composition, are also universal physical principles, so defined by their physical effects on the potential relative population-density of societies (“cultures”). Both these classes (sub-phase-spaces) of universal physical principles, are to be located within the anti-Euclidean physical geometry defined by Bernard Riemann.11
- The physical effects of the combination of those first and second sub-phase-spaces, are measured with reference to the long-term (multi-generational) increases (or decreases) per capita and per square kilometer of the Earth’s surface: what I have defined as the potential relative population-density of our species. The discovery of this twofold set of principles as an integral notion of function to that intended effect, has been my original contribution to a science of physical economy.
- The social transmission of the first class of principles, by means of the second, defines the efficient actuality of the historical existence of our species, and thus defines the uniqueness of the human species. This transmission is the elementary basis in fact for both a history of science and a science of history.
For today’s populations, the two sets of principles just identified, are more easily understood by aid of references to my own, critical appreciation of the work of Vladimir Vernadsky’s respective, successive definitions of the Biosphere and Noösphere. However, there are three crucial omissions of essential principle in Vernadsky’s known writings, principles which were featured as central to my own original discoveries in the science of physical economy. Nonetheless, Vernadsky’s work, if and when taken in the context of my own, is of crucial importance for inclusion in teaching my own discoveries to university-level studies today. My exposition here follows that pedagogical track, as in earlier locations.12
For reasons which I shall summarize here, the appropriate approach to study of the case of Gauss’s 1799 attack on the systemic fallacies of such anti-Leibniz fanatics as the reductionists Leonhard Euler and Euler’s protégé Lagrange, serves today’s student of university age, or a relatively exceptional secondary student, as the best point of entry into the foregoing list of categories of knowledge. A clear insight into Gauss’s discovery reported there, requires a direct comparison of the equivalence of Abraham Kästner’s student Gauss’s attack on the axiomatic errors of d’Alembert, Euler, and Lagrange, to the earlier, Classical arguments to similar effect by such Classical Greeks as Archytas and Plato on the matters of methods of construction for doubling the geometric figures of line, square, and cube. This comparison must include Plato’s, Leibniz’s, and Gauss’s mutually congruent, anti-Aristotelean notion of powers for these cases.13
The foregoing prefatory remarks mark out the territory to be covered. What now follows is a combination of arguments presented in locations previously published, with some added points needed to bring the totality together in that kind of unified world-outlook which ought to become the common basic knowledge of persons of the 18-25 age-interval of education today.
In the Beginning: Plato’s
Principle of Hypothesis
The sense organs of the human individual are part of the mortal human being’s animal-like, biological organism. Sense-perception does not present our mind with direct images of the world “outside our skins,” but rather, as Plato and the Christian Apostle Paul’s 1 Corinthians 13 warn, our senses show us only “shadows” of that reality which has tickled the human individual’s biological mental-sense-perceptual apparatus. So, Plato compares the experience of sense-perception to shadows cast by unseen real objects, as if upon the walls of a dimly firelit cave.
Human beings are nonetheless capable of discovering the real, essentially unseeable, immortal universe whose included, non-substantial effects are those shadows called sense-perceptions. The method by which those discoveries are made, is typified by the Socratic dialectical method of Plato, otherwise known as the method of hypothesis. Plato’s collection of Socratic dialogues, and his Laws, constitute a body of exemplary mind-training exercises, by which the student is aided in attaining comprehension of scientific method. As I shall show, later in this present report, Vernadsky’s definition of the Noösphere implies a strictly physical-scientific definition of the meaning of “spiritual.” These same Socratic exercises which are the centrally characteristic feature of the discovery and transmission of experimentally validated universal physical principles, are therefore to be recognized as “spiritual exercises.”
Among Plato’s dialogues, his Parmenides has special relevance for that aspect of our report. In that dialogue, Plato implicitly emphasizes the importance of the development of scientific method by Thales’ follower Pythagoras, a connection which has crucial significance for Gauss’s referenced, 1799 definition of the complex domain. The most crucial of the known ancient discoveries, are the fruit of a class of paradoxes of geometry, including the Pythagorean experimental demonstration of the paradoxical musical “comma,”14 and the impossibility of reductionist solutions for such paradoxes as: the doubling of the line, the square, and cube, and the construction of the five Platonic solids. Despite the claims of the followers of Euler, Lagrange, and Cauchy, no competent solution for these paradoxes is found by means of a geometry confined by “ivory tower” definitions inhering in the shadowy, axiomatically erroneous presumptions of the reductionists’ sense-perception.
Gauss’s discovery of the physical principle of the complex domain, as in the referenced 1799 piece, returns our attention to the Classical Greek form of the elementary paradoxes of doubling of the line, square, and cube. These ancient paradoxes are indispensable keys to defining a form of modern mathematical physics, that of the complex domain, which is capable, axiomatically, of functional representation of the real universe, as can not be done competently by the ivory-tower imageries of errant mathematical reductionists such as Euler and Lagrange, and their present-day followers.
Consider the relationship between Plato’s method and that of such of his modern followers as Brunelleschi, Cusa, Pacioli, Leonardo da Vinci, Kepler, Gilbert, Fermat, Huyghens, Leibniz, Jean Bernouilli, Abraham Kästner, Gauss, Lazare Carnot, Dirichlet, and Riemann. Contrast this to that fanatical sort of axiomatic error of “ivory tower” reductionism, which is common to ideologues such as Aristoteleans, and such empiricists as Descartes, Newton, Boyle, Euler, Lagrange, Laplace, Cauchy, Clausius, Grassmann, Helmholtz, Maxwell, Lindemann, Felix Klein, and the devotees of Bertrand Russell. Focus upon the most essential point of irreconcilable conflict in method between the two sets. Then examine those implications of that contrast which are illuminated by the methods employed by Vernadsky to define the Biosphere and Noösphere.
What Is Hypothesis?
The discoveries of Johannes Kepler, effected by the methods he details in his 1609 The New Astronomy, were the beginning of a comprehensive form of mathematical physics. As in all science, so in contrasting the success by Kepler to the failed method of Claudius Ptolemy, Copernicus, and Brahe, we must take into account the relevant ancient precedents for the follies of such followers of the ancient Eleatics as the modern empiricists Galileo, Descartes, Euler, and Lagrange. We must give our attention to what many famous names in history have easily overlooked among the ostensibly fine details of scientific rigor. Those paradoxical details in methods of observation and judgment, are usually the key to truly important discoveries, even validatable discoveries made by confessing religious empiricists. Even reductionists such as Aristotle and the empiricists, sometimes admit the paradoxical existence of efficient principles which can not be observed by the senses, if not those principles themselves. Like the Romanticist Immanuel Kant, they either concede, or claim to know of, the existence of such considerations, which they define wrongly, while insisting that such agencies, if they exist, can not be known rationally by the individual human mind.
Apart from the specific wickedness of Aristotle’s Politics and Ethics, the general folly of Aristotle’s method for physical science itself, is typified by Claudius Ptolemy’s hoax. Although Aristotle assumes a higher reality than sense-certainty to exist, Ptolemy follows Aristotle in limiting attempted knowledge of actual physical principles to a kind of apparent statistical regularity presumed to be consistent with the introductory books of Euclid’s Elements. Although Copernicus echoes the heliocentric view of Aristarchus, the astronomy of Copernicus and Brahe accepts the same anti-scientific quality of “medieval” method of Aristotle, adopted by Ptolemy.
Within his The New Astronomy and other published locations, Kepler presents an elaborate report on the anti-scientific character of Aristotle’s doctrines; Gauss, in developing a crucial proof of the entirety of Kepler’s argument respecting the functional composition of the solar system, applies the case of the principal asteroids as the empirical proof underlying Kepler’s definition of the principles of a comprehensive approach to mathematical physics.15
The errors of Aristotle’s method are always found in the details which that method either presumes to deny, or relegates to the domain of the humanly unknowable.
The followers of that Ockhamite perversion of Aristotle called empiricism, as typified by Paolo Sarpi, by Sarpi’s personal lackey Galileo Galilei, Galileo’s pupil Thomas Hobbes, and Locke, turn Aristotle’s details into what often prove to be explicitly an actively nasty sort of what is literally a “devil in the detail.” For example, Anglo-Dutch Liberal John Locke makes implicitly a neo-Cathar argument which is featured explicitly as the central claim of Physiocrat François Quesnay. The same neo-Cathar claim is featured shamelessly in the central arguments for “free trade” by such of Locke’s fellow-Gnostic followers as the more frankly pro-Satanic Bernard Mandeville, and Mandeville’s follower Adam Smith.16
Quesnay is a shameless devotee of the ultramontane medieval feudal system of serfdom. His Physiocratic scheme explicitly classes the serf, axiomatically, as a form of human cattle. To support that argument, his absolutely irrational, laissez-faire defense of feudal parasitism, resorts to copying the dogma of the neo-manichean cult of the Cathars.17 He, like a Cathar, defines a capriciously corrupt deity, a nasty sort of gnome operating from under the floorboards of reality, who “fixes” the throw of his crooked dice, such that some people are made, magically, rich and powerful, while others are left destitute and poor. Modern Liberal economists describe that swindle as “statistics.”
The “Venetian Party’s” John Locke, Mandeville, and Adam Smith, are not customarily regarded as traditional feudalists like Quesnay; but, they share with Quesnay a common interest in their hatred of the Fifteenth-century Renaissance and of, more immediately, the existence of France’s Cardinal Mazarin and Jean-Baptiste Colbert. These “Enlightenment” Liberals are all, like John Locke himself, typical of the philosophical expressions of that neo-Venetian form of Anglo-Dutch Liberalism which raged, like a pandemic, across the maritime regions of late-Seventeenth- and Eighteenth-century northern Europe, and spread into the endemically treasonous Essex Junto and slave-owner circles in English-speaking North America. The neo-manichean doctrine of Quesnay appears in a Liberal guise as the explicit advocacy of moral depravity in Mandeville’s The Fable of the Bees, as the same pro-serfdom dogma of the Physiocrats is echoed in Liberal John Locke’s defense of slavery as “Property.”18 Quesnay’s and Mandeville doctrine of “let the Satan whom Smith esteems as the knowing Director of nature, fix the dice,” is echoed by Adam Smith’s 1759 The Theory of the Moral Sentiments, as in his anti-American tract of 1776, The Wealth of Nations.19
To situate the subject-matters thus introduced, we must recognize that any attempted attack on the problems of physical science, such as physical economy, requires that so-called physical science and so-called social theory not be kept in separate, virtually water-tight, academic compartments. On this account, a competent understanding of both so-called “physical science” and “social theory,” depends upon viewing both, simultaneously, as I have done, from a common axiomatic basis in the standpoint of the pre-Euclid geometry of Plato’s Academy.20
The modern reductionist standpoint, typified by Galileo and Descartes, assumes, as Ptolemy’s, Copernicus’s, and Brahe’s schemes did, that individual sense-experience can be represented by a set of putatively “self-evident” definitions, axioms, and postulates, and, therefore, that a sufficiently well-developed mathematics, derived from such a set of “ivory tower” presumptions, such as that of the reductionists Euler, Lagrange, and Cauchy, must, as Lagrange taught, be potentially capable of explaining comprehensively anything and everything which occurs with the bounds of sense-experience. No hypothesis allowed!
In contrast to Lagrange et al., the standpoint of the school of Thales’ follower Pythagoras, accepts no “ivory tower” assumptions. Typical of the anti-Euclidean physical geometry of the Pythagoras-Plato tradition, are the same three elementary challenges by means of which Gauss, in 1799, defines the complex domain: the doubling of the line, the doubling of the square, and the doubling of the cube, as defined by Plato’s collaborator Archytas, the Pythagorean of Tarentum. Add to this the uniqueness of the five regular (Platonic) solids. For Plato’s view on these, consider three of Plato’s dialogues, where the anti-Euclidean principles of physical geometry are referenced: the Meno, Theaetetus, and Timaeus. Read Gauss’s fundamental theorem of algebra against that background; read the powers of the square and cube as they are expressed in an algebra so considered, or, as Gauss’s famous, and crucial two documents on bi-quadratic residues, presents this view. The solution for the physical act of construction of the doubling of the cube, which resolves the so-called “Cardan problem,” presents the student with a sense of the efficient “physical presence” of the same complex domain in which Leibniz had located the catenary-keyed expression of a universal physical principle of least action.
The mastery of those elementary challenges of a purely constructive geometry, is to be taken against the experimental background of Fermat’s, Huyghens’, Leibniz’s, and Jean Bernouilli’s demonstrations, that physical effects in the universe do not follow a pathway of “Euclidean” (e.g., “Cartesian”) pathway of “shortest distance,” but of “quickest action,” a pathway of action which scientific progress typified by the characteristic figure of physical geometry, the catenary. What needs to be purged from education, is the moral degradation of the teaching and application of mathematics to a mere describing of nature, as the Newtonian tradition of Lagrange’s dogma does. In other words, as I shall stress at appropriate places in my argument here; the sterile mathematics of mere “energy,” must be superseded by the physical geometry of “power.”
The implication of such lessons, is that the principles of space-time organization lie in physical space-time, not a space and time of “purely mathematical,” “ivory tower” definitions, axioms, and postulates, on which latter, false presumptions, the relevant failures of d’Alembert, Euler, and Lagrange were premised, as were the failures of such followers of Lagrange as Laplace, Cauchy, et al. Contrary to Aristotle, Euclid, and the “non-Euclideans,” competent mathematical knowledge can be obtained only by those experimentally verified methods of constructed proof of principle which are reflected in the Platonic argument of Gauss’s 1799 paper. The outcome of Gauss’s work to this effect, becomes the opening paragraphs of Bernard Riemann’s 1854 habilitation dissertation, which presents a general definition for a purely anti-Euclidean, rather than “non-Euclidean,” physical geometry.
A physical geometry limits the notion of “dimensions” to those hypotheses, as Plato defines a notion of hypothesis, which occur as the acts of discovery and experimental proof of universal physical principle. These acts must have been validated, as Riemann emphasized, by methods of experiment uniquely appropriate for general claims to a proposed principle’s universality. The discovery of the method of construction which enables a human mind to double a line, square, or cube, by no means but construction, defines “properties” of each, which are expressions of the powers of physical action by means of which relevant construction is accomplished. For example, the sublime “power” which distinguishes rotation from a mere line, and a solid from a mere surface. Gauss’s treatment of the cubic function, and also his construction of the Pentagramma Miraficum, are typical illustrations of the use of the principle of construction as a reflection of physically efficient effects of “powers.”
Successful hypotheses begin with a paradox. For example, does a cube exactly double the volume of a given cube, actually exist? Think about that; it is not an idle question. Prove it by construction! Look at Archytas’s solution for this! The method of construction which solves that specific paradox expresses an experimentally demonstrated hypothesis which guided Archytas to that solution [See Figure 1].
| Archytas developed a construction to find two geometric means between two magnitudes, AC and AB. Magnitude AC is drawn as the diameter of circle ABC; AB is a chord of the circle. Using this circle as the base, generate a cylinder. the circle is then rotated 90° about AC, so it is perpendicular to the plane of circle ABC; it is then rotated about point A, to form a torus with nil diameter. (The intersection of the torus and the cylinder produces a curve of double curvature.) Chord AB is extended until it intersects the perpendicular to AC at point D; this forms triangle ACD, which lies in plane of circle ABC, AB, and AC. Triangel ACD is then rotated around AC, producing a cone. The cone, torus, and cylinder, all intersect at point P. Perpendicular PM is then dropped from P along the surface of the cylinder, until it intersects circle ABC at point M; this forms right triangle AMP.
Through this construction, a series of similar right triangles (only partially shown) is generated, which produces the continued proportion, AB:AM::AM:AP::AP:AC. AM and AP are the two geometric means between magnitudes AC and AB. |
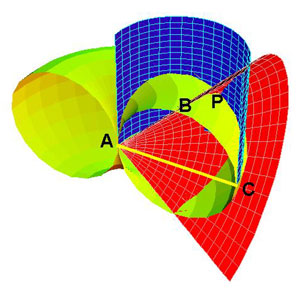 |
That which is presented to the senses of the purblind newborn child is a realm of paradox-ridden sense-impressions, not a faithful image of the world outside his skin. The child must not only discover the functional relations within sensed physical space-time; he, or she must repeatedly rediscover those relations, correcting earlier errors of presumption in a succession which suggests the peeling of the onion. From the beginning, the child’s mind must hypothesize the existence of that which corresponds to the always paradoxical sense-experience of that real, unseen physical space-time which tickles the human sense-apparatus. Nothing real is simply self-evident.21
New dimensions of physical space-time exist for us only as we acquire those new willful powers over nature which we define as the successive work of Gauss, Dirichlet, and Riemann defines a physical universe of that expanding array of paradoxes. These are paradoxes which the human will has either mastered as human physical powers for hypothesizing in the universe, or are, at the least, recognized challenges, as those paradoxes which we are seeking to bring under the willful control made available to us by experimental proof of physical principle.
That, in short, is the issue of hypothesis which almost invariably prompts the wildest eruptions of distemper among the reductionists of the “pure mathematics” and “physics” departments. What enrages those “ivory tower” fanatics, is their confrontation with the details which threaten to topple the edifice of their “self-evident,” mathematical “ivory tower” conceits.
That much said, what then is the way we must define the relations between what is usually assigned to the department of mathematical physics, as distinct from what is assigned to the departments of taught social dogma? A glance at Kepler’s method will point the way.
Kepler and Prometheus: A Matter of Detail
Kepler’s attention to detail showed him the existence of some crucial oversights in the work of astronomer Tycho Brahe. The orbit of Mars was not circular, but approximately elliptical. Moreover, the motion of the planets in their elliptic-like orbits was not uniform, but constantly not uniform. Nonetheless, the succession of the recurring orbits was predominantly regular. These elementary details showed that the real universe did not function as Aristoteleans such as Ptolemy, Copernicus, and Brahe had imagined. The real universe was not the universe as a naive Aristotelean or empiricist blind faith in sense-certainty misdefines the notion of what are called “universal principles.”
In brief, Kepler recognized the paradox of observed, approximately elliptical orbits, that, not only, can the notion of Aristotelean regularity never be reduced to a simple form of action, but that, more to the point, the characteristic principle of action in the more scrupulously observed solar system, is expressed by constantly non-uniform motion. The shadows on the screen of a merely perceived solar system’s motions, are therefore controlled by some universally efficient power, in Plato’s sense of “power” (as contrasted with the reductionist notion of mere “energy”). Kepler recognized the object which cast the shadows of astronomical sense perception as a controlling intention of the Creator of the universe: a universal physical principle, a power acting efficiently from outside perception, to produce the shadowy effects presented to the astronomer’s perception.22
The intention, which must be discovered, and then proven to be universally efficient in controlling the behavior of the shadows, appears first as a paradox, and then as an hypothesis which needs experimental proof of its efficient universality.
That much, for the moment for that example from Kepler; now, for LaRouche on the Riemannian geometry of long-range capital cycles.
What is an experimental proof of a Platonic quality of hypothesis? Really? Here, on this crucial point respecting the implications of experimental proof of principle, the Aristoteleans and empiricists figuratively hang themselves. The validity of the claim to have discovered any universal physical principle, is not satisfied by the mere repetition of the specified, observed effect. It must be demonstrated that the application of what is believed to be an individual’s discovery of a proven universal physical effect, enables mankind to increase its power to exist in the universe. It must be demonstrated that the claimed hypothetical knowledge represents a principled increase of mankind’s power to exist in the universe, as Plato defines “power” where the erring Aristotle claims to see “energy.”
In the relatively simplest case, the notion of power, as employed by Plato’s dialogues in respect to doubling the square, or the Pythagorean Archytas’s construction of the solution for doubling of the cube, represent pre-existing principles of the universe, but preexisting universal principles whose discovery enables man to produce effects which are changes in that otherwise preexisting universe. The elementary cases of doubling the line, square, and cube, by construction, are typical of such Platonic connotations of power.
To illustrate the point of contention, consider the implications of what I have just said. Consider the legendary image of Prometheus, a subject to which I shall return at a later point here. The mention of that name now cracks the egg-shell, releasing our thoughts into a larger universe. This takes us directly to the most essential implication of Riemann’s 1854 habilitation dissertation.
Economist LaRouche’s View of Our Universe
Now, we come to the point of this report at which we shall focus upon the idea of measurement of performance of economies in physical, rather than fictitious, financial-accounting terms [See Figures 2-5].
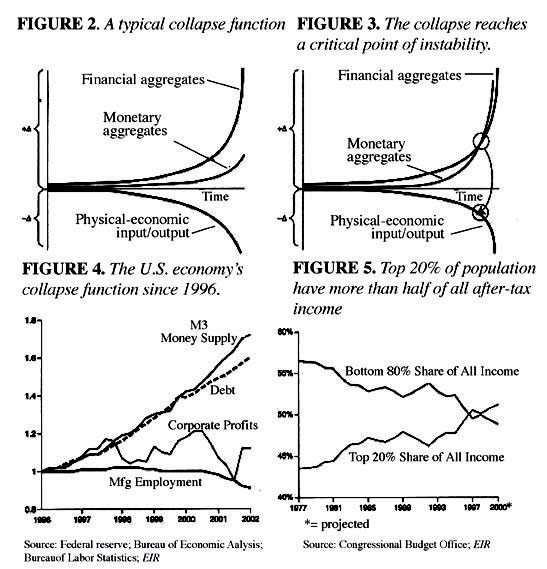 |
| Over the 1966-2002 interval, the nominal values of U.S. financial and monetary growth zoomed, while the net physical values per capita collapsed. The financial crises of President Clinton’s tumultuous second term, 1997-2000, culminating in the collapse of the “Y2K/Infotech” and “hedge fund” financial bubbles, were essentially a culmination of a long process of degeneration of the U.S. economy’s physical basis, as reflected in the collapse of share of income of the lower 80% of family-income brackets. |
This clarification of the principles of real, as opposed to financial-accounting economics, requires a careful, preliminary reconsideration of some of the most important of the underlying considerations of physical-scientific practice. The indispensable role of the discussion of these considerations for any science of economy, will be made clear in the course of both the immediately following, concluding topics of present chapter, and subsequent, concluding chapter of this report.
We proceed, at this point, by turning first to an indispensable set of remarks on the nature of science in general. This applies to both matters of the phase-space of the individual’s action on the universe, and the physical effects determined by the principles of the social processes within which individual action is situated.
In any competent aspect of physical science, even formal mathematics, nothing exists before, after, or outside our universe. Einstein’s notion of the universe (taken as a totality) as “finite, but unbounded,” reflects such an awareness of the framework within which we might conduct any rational discussion of the universe. Similarly, if we must suppose that that universe always existed entirely within itself, that is not to suggest that it did not continue to develop, but that it is a Riemannian universe, producing not only new forms, but changes in characteristics of action within itself.
Suddenly, with that latter thought, of development, the universe becomes a fascinating place of residence; physical science suddenly comes to life. Our notions of matter, space, and time, are changed profoundly, both individually, and in respect to their functional interconnections. Those childish notions of space and time which occupy popular and other scientifically illiterate opinion today, vanish, replaced by something which Riemann’s notions of physical geometry suggest.23
For us, as mortal human beings, all that science has discovered so far to be universal physical principles, points to principles which must be presumed to be, and should be tested for the quality of being universal, in their efficient extent of relevant application. Therefore, for a qualified physical economist, any Platonic form of hypothesis which is proven to be a universal physical principle by Riemann’s implied standards of unique experiment, always existed within “the simultaneity of eternity,” with those qualifications, and always will. This is to be understood in the sense that Gauss’s 1799 report of the discovery of the fundamental theorem of algebra signifies “universal physical principle” in a Platonic way which reflects the Classical Greek constructions of Archytas, Plato, et al. That presumption of universality will remain true, to the extent some qualifying error in the interpretation of that notion were not uncovered and corrected.
Therefore, in the subject-area within which this report is situated, the practice of economic science, we must proceed from the conditional, pragmatic assumption, that man probably does not create new general types of universal physical principles for the universe, but, rather, is able to create new physical states in the universe, through Platonic modes of discovery and application of pre-existing natural principles. Man extends the actual application of those discovered, universal principles which have the character of Platonic powers. This is the central principle of practice for both economic science today, and the principle governing the determination of relevant forms of competent law and policy-shaping practices of governments. Pending new discoveries which extend knowledge of our universe beyond that available today, this view expresses the principle on which the competent measurement of performance of an economy must be measured currently.
Therefore, the conditional notion of science today, must limit its claimed ambitions, to the bounds of those universal new states in the universe, which our discovery of pre-existing principles enables us to introduce as qualitative changes in our practice upon the universe. All competent notions of economic processes depend directly and absolutely on that view of man in the universe as a whole.24
The essential argument to be made here respecting elementary principles of a science of physical economy, is summed up as follows.
When a person discovers an experimentally validated universal physical principle, a Platonic quality of power already existing in the universe, it is placed implicitly at the disposal of mankind. The best evidence of history to date, is that this action adds no new principle to the total of those existing in the universe, but increases the powers of the universe now placed within the domain (Riemannian phase-space) of powers now at mankind’s willful disposal.25 The realization of that new potency of mankind produces qualitatively new states within the universe, states which would not be generated without man’s practice of those principles. This changes the behavioral characteristics of that universe in a principled way, without yet increasing the totality of principles existing in the universe.26
A related, if more limited conception of the universe, is presented by Vernadsky’s successive development of the conceptions of Biosphere and Noösphere.27 Vernadsky, a trained geologist, proceeding from the included benefit of the accomplishments in geology and physical chemistry of his former teacher Dmitri I. Mendeleyev, took up the work of Louis Pasteur et al., in defining the existence of life as a distinct universal principle, not derived from an abiotic universe. To this end, as a physical chemist of that intellectual pedigree, he introduced the case for the existence of what he identified as the Biosphere, whose geological “history” shows the abiotic processes of Earth as under increasing relative domination by the combination of the totality of living processes and their fossils, the latter including our planet’s atmosphere, bodies of water, and soils.
As this fact became relatively well known among scientifically literate university graduates of the last half-century, the kernel of this notion of life as an expression of a primary form of universal physical power,28 is that what are known to be living processes, produce what are otherwise impossible states of organization among non-living processes. This conception, whose development relevant classrooms and textbooks have traced to outgrowths of the initiatives of Pasteur, was pursued by his associates and followers such as Curie, to the effect of defining life as a specific quality of universal principle (power).29
Following the introduction of the reductionist notion of thermodynamics, by Clausius, Kelvin, et al., the experimentally based mathematical-physics distinction of life from abiotic processes generally, was early associated, by friends of life, with a mathematical notion originally named “negative entropy.” This distinction presumed that life is a self-subsisting universal principle, not dependent upon specifically abiotic assumptions, which is imparted by life to the universe as a whole. Later, from the late 1940’s onward, as the crankish, radically positivist, anti-humanist notions of such followers of the fanatical Ernst Mach as Ludwig Boltzmann, and Bertrand Russell’s devotees such as Professor Norbert Wiener, and John von Neumann, gradually gained broad, even popular currency, the original experimental connotations of “negative entropy” have almost disappeared from general use. That term has been taken over by the popularization of the pathetic science-fiction cults of the positivists, not only among science-illiterate politicians and mass-media editors, but even among many persons who are putatively actual scientists.
To eliminate that growing confusion caused by the spread of the “information theory” fads, as through the irrational fantasies of “science fiction” writers and their readers, I found myself compelled to introduce a new, mathematically more precise term, “anti-entropy,” for what had been the biologists’ original, pre-“information theory” intent of “negative entropy.” I premised this notion of “anti-entropy” on the characteristic functional distinction between an anti-Euclidean physical geometry, notably that of Gauss-Riemann, from a merely “non-Euclidean” geometry, such as those of Lobatchevsky, Janos Bolyai, and Hermann Minkowski’s famous lecture on relativity. This notion of “anti-entropy,” as it must be identified today,30 reveals its essential role in defining universal physical principles when we recognize two inseparable notions, as Vernadsky did, in his defining a Biosphere.
The fact, that processes characteristic of life generate ordered states of nature not existing in abiotic processes, not only defines living processes, but also provides a rigorous line of experimental division between abiotic and living processes. This line of division has the quality of a universal physical principle of the type associated with the notion of a power in the physical geometry of Plato, Kepler, Leibniz, Gauss, Dirichlet, and Riemann, among others. First: It identifies an expressed power which is always functionally characteristic of the living process, but never the abiotic as such. Second: As Vernadsky showed the proofs of this fact, the biological evolution of our planet, when the fossils specific to living processes are counted in, increases the accumulation of biomass, including such fossils as atmosphere and oceans, the living process dominates the abiotic in long-term effects of this transforming of the planet.
This division between the abiotic and living separates the phenomena of Vernadsky’s Biosphere into two distinct but universally interconnected, Riemannian phase-spaces. Vernadsky’s work shows no actual comprehension of Riemannian physical geometry and its implications, but his work begs rereading from the anti-Euclidean standpoints of Kepler, Leibniz, Gauss, Riemann, et al.
Vernadsky’s approach to the Biosphere leads him toward defining the Noösphere.
Just as the physical effects of action of living processes, produce the combination of living processes and their fossils, so what Vernadsky identifies as the distinctive creative (noëtic)31 powers of the human mind, produce qualitative changes in the combined processes of the Biosphere, changes representing physical effects which can not be the spontaneous outcome of living processes alone. The combined effect of these noëtic and Biosphere processes, produces what Vernadsky defines as the Noösphere. The result is the image of a three-phase universe, the Noösphere, composed of the interconnected action of three distinct phase-spaces: abiotic, living, and noëtic.
Where Vernadsky writes noëtic, I point to the quality of mental action typified by Gauss’s 1799 exposure of the anti-creative physical-scientific impotence of Euler, Lagrange, et al. in the matter of those universal physical powers which are reflected in the reality of the complex domain. Gauss, like Leibniz before him, and such successors as Riemann, moved science toward eradicating all “ivory-tower” definitions, axioms, and postulates from science, and replacing these with nothing but those discovered universal physical principles defined by experimentally validated Platonic forms of hypothesizing: noësis.32
It is that specific quality of creative reason which places Euler and Lagrange in stubborn defiance of the existence of human creative reason, as Gauss’s cited 1799 argument typifies the product of creative reason, which otherwise is key to locating the functional difference between man and beast. This takes us beyond the accomplishments of Vernadsky, into the domain of Riemannian physical geometry. This is also the key to a competent economic science.
|
Footnotes |
||
1. The corrupting influence of McGeorge Bundy’s Ford Foundation on U.S. educational practices over the late 1960’s and 1970’s, should be seen as complementing the disastrous influence of Britain’s Dr. Alexander King’s 1963 Paris OECD report on education in Western Europe, as the effect of the latter is typified by Germany’s disastrous “Brandt reforms.” King was a co-founder, with Lord Solly Zuckermann, of the neo-malthusian Club of Rome, and was associated with Zuckermann, the U.S.A.’s McGeorge Bundy, and others in forming the pro-malthusian, Laxenberg (Austria)-based International Institute for Applied Systems Analysis (IIASA). IIASA was the Lord Kaldor-featured Cambridge Systems Analysis group’s strategic back-channel to the Moscow malthusians. The corruption is to be recognized as typical of the moral self-destruction carried out simultaneously on both sides of the Atlantic, and also both sides of one-time British Prime Minister Winston Churchill’s “Iron Curtain.”
2. This cultural-paradigm shift was a complement to the “preventive nuclear war” doctrine of avowed nuclear terrorist and pacifist Bertrand Russell, which became the core of the “Dr. Strangelove” (Leo Szilard) style nuclear-utopian strategic military and cultural doctrines of the anti-traditionalist, so-called “utopian” military-policy faction of the 1944-2002 interval.
3. The Gospel of John and the Epistles of Paul typify this most clearly. However, the Platonic tradition is also an ecumenical one, as typified by Philo of Alexandria and Moses Mendelssohn for Judaism, and also Islam.
4. Cf. two works by the anti-Kantian Heinrich Heine: The Romantic School, in The Romantic School and Other Essays, ed by Jost Hermand and Robert C. Holub (New York: Continuum, 1985); and Religion and Philosophy in Germany: A Fragment, trans. by John Snodgrass (Albany, N.Y.: State University Press of New York, 1986). Emphasis should be placed on Heine’s own first edition of the latter work.
5. Cf. Jonathan Tennenbaum and Bruce Director, “How Gauss Determined the Orbit of Ceres,” Fidelio Summer 1998 (Vol. VII, No. 2).
6. Out of compassion for the incompetents teaching in those economics departments, we should emphasize the virtually criminal kind of intentional statistical fraud practiced over the recent two decades by the Federal Reserve and other malefactors under such rubrics as the so-called “Quality Adjustment” factor.
7. It is notable, respecting lessons for educational policy generally, that an approximately year-long recovery and rehabilitation from a severe case of hepatitis, imprisoned me in circumstances under which recreation often took the form of extended, increasingly intense concentration on the relevant implications of the work of Georg Cantor and Bernhard Riemann for physical economy. This occupied most of the waking hours during the several initial months of recuperation, and reenforced greatly the habits of study and work which have dominated my life since.
8. The reader should understand “long-range” forecasts to be based on the effect of current, implicitly axiomatic assumptions of a society’s economic behavior over a span of one to three generations. Approximate forecasts for periods as short as three to seven years are feasible. For example, in February 1982, I first warned the Soviet government, during my part in a 1982-1983 back-channel discussion which I conducted on behalf of the Reagan Presidency, that if the Soviet Andropov government continued the policy its representative had reported to me, that the Soviet-bloc economy would collapse in “about five years.” I subsequently made the same forecast publicly. On the basis of that forecast, I warned, in an October 12, 1988 Berlin press conference, later broadcast on U.S. network TV, that the policy of the next U.S. Administration must base its policy-shaping on the expectation of an imminent collapse of the Soviet bloc economy, with Berlin to become the expected future capital of a reunited Germany. This case illustrates the point, that competent short-to-medium-term economic forecasts are possible only as they are subsumed by study of long-term capital/generational factors. In the short-to-medium term, the factor of human “free will” may produce immediate effects contrary to nonetheless persisting long-term “orbital trajectories.”
9. While this report was being written, I received several draft papers, of David M. Shavin and other collaborators, on the subject of my own and my associates’ continuing fascination with the influence of Leibniz, from Europe, expressed in both the U.S. Declaration of Independence and U.S. Constitution, and in the principles of what Alexander Hamilton defined officially as the American System of political economy. My associates’ continuing attention to these connections, which had been spearheaded by historian H. Graham Lowry during the early 1980’s, will be featured in an edition of the Fidelio quarterly to be released from the printer during February 2003 [Fidelio, Spring 2003 (Vol. XII, No. 1)].
10. Although the reductionists, such as Lagrange himself, Laplace, Cauchy, Lindemann, Felix Klein, et al., have rejected the crucial kernel of Gauss’s 1799 argument, no competent objection to Gauss’s proof is known, to the present day.
11. My use of “Classical” is a strict one, as I indicate below. As I shall show during my summary of the lessons to be adduced from Vernadsky’s definition of the Noösphere.
12. Lyndon H. LaRouche, Jr., The Economics of the Noösphere (Washington, D.C.: EIR News Service, 2001).
13. Abraham Gotthelf Kästner (b. 1719) is a key international figure behind such of his students as Lessing and Gauss, and a central figure in the Eighteenth-century development of mathematical physics. He was a crucial influence in the Eighteenth-century rise of the German Classic around Lessing and Moses Mendelssohn, and played a pivotal role in bringing knowledge of the work of Leibniz into the leading circles of the American Revolution. Among Kästner’s many important publications, the most notable, which should inspire some noble souls to produce good English language translations, include his 1758 Anfangsgründe der Arithmetik, Geometrie, ebenen und sphärischen Trigonometrie, und Perspective and his four-volume Geschichte der Mathematik, Vols. I-IV (1796-1800). Kästner was the founder of an explicitly anti-Euclidean geometry; his influence on his pupil Gauss on this account, is reflected in Gauss’s own discovery of elements of an anti-Euclidean geometry, dated to 1792, and reflected in Gauss’s 1799 refutation of the reductionist errors of Euler and Lagrange. Riemann’s development of an anti-Euclidean, as distinct from merely “non-Euclidean” geometry, is chiefly an outgrowth of this line of development by Kästner, Gauss, and Dirichlet. Kästner was also a crucial collaborator of Benjamin Franklin, as a forthcoming report by my associates will pin-point this crucial connection of the anti-Locke influence of Leibniz in defining the 1776 U.S. Declaration of Independence [Fidelio, Spring 2003 (Vol. XII, No. 1)]..
14. The relevant experiment is Pythagoras’s comparison of various orderings of what must have been the equivalent of Florentine bel canto-trained singing voices, in various modes, against a monochord. The naturally determined differences in intervals of the singing voice, compared with the relevant lengths marked off on the monochord, would define a “comma,” not as a mathematically predetermined, but physically lawful characteristic of the properly developed human singing voice. The related case for J.S. Bach’s well-tempered system, as opposed to the reductionist system of equal-tempering, an example of the same principle. Hence, the “comma” is an example of the difference between a physical geometry, and an “ivory tower” geometry.
15. Cf. Johannes Kepler, The New Astronomy; see also Tennenbaum and Director, op. cit. Implicitly, Gauss’s confirmation of Kepler’s case for “the missing planet,” in the orbits between Mars and Jupiter, is an application of the notion of the complex domain which Gauss had presented, in refutation of Euler and Lagrange, in the 1799 piece.
16. As I have elaborated this in locations published earlier, the use of the term “capitalism,” as Karl Marx does, to describe, implicitly, both the Constitutional economic system of the U.S.A. and the present systems of western Europe, shows the speaker to be either illiterate in the most elementary features of modern economy, or a shameless liar. The crucial, continuing issue of U.S. wars against the British monarchy is rooted in the axiomatic incompatibility of the British system to that U.S. Constitutional system, rightly known to scholars by the names of “The American System of political-economy” or “the national system of economy.” The principal objectionable feature of the British system was, and remains, its foundations in that neo-Venetian system of Anglo-Dutch Liberalism, in which a financier slime-mold form of oligarchy controls the fate of the nation and its other victims through the agency of an “independent central banking system.” The latter system represents the special interest of a Venice-style financier oligarchy, which places itself above government in the foreign and internal affairs of both the nation and foreign targets, alike. This oligarchical feature is the notorious “Invisible Hand” (the one presently in your pocket). Under the U.S. Constitution’s Preamble, the U.S. government is the sole sovereign, which is accountable to the interest of the General Welfare of present and future generations. Admittedly, the U.S. Federal System, introduced by U.S. agents of Britain’s Edward VII, is an abomination, but, since its constituent private shareholders are presently hopelessly bankrupt, the sovereign’s authority expressed by the U.S. Treasury should be putting the embarrassed Fed under bankruptcy-reorganization, soon.
17. In English slang, “the buggers.”
18. E.g., “shareholder value.”
19. Cf. Friedrich August Freiherr von der Heydte Die Geburtsstunde des souveränen Staates (Regensburg: Druck und Verlag Josef Habbel, 1952). My wife, Helga Zepp LaRouche and I have compared leading international law specialist von der Heydte’s thesis to our own emphasis on the Fifteenth-century Renaissance. The two views, his and ours, are more complementary than contrasted. He emphasizes the struggle to free Europe from continued enslavement by the imperial law which ultramontane feudalism continued under the tyranny of (in our emphasis) Venice and the Norman military forces. The Fronde adversaries of a modern form of French nation-state, and of Cardinal Mazarin and Jean-Baptiste Colbert, who later allied against Colbert with the Gnostic “Sun King” Louis XIV, were a typical expression of the ultramontane tradition. Notably, the explicit coincidences of the Physiocratic tradition of Quesnay and Turgot, with the explicit “buggery’ of Mandeville and Adam Smith, reflects the Venetian oligarchical roots common to both the ultramontane feudal and Anglo-Dutch Liberal systems.
20. Benjamin Franklin collaborator, and Leibniz follower Abraham Kästner’s crucial, leading role in the middle- through late-Eighteenth-century development of both Europe’s Classical science and art is strongly implied here. It was Kästner who insisted that mathematics should abandon the post-Plato, “ivory tower” system of definitions, axioms, and postulates introduced as Euclid’s Elements, and return to a strictly Platonic, anti-Euclidean conception of the experimentally based discovery of universal physical principles (powers). Hence, the development of an actually anti-Euclidean physical geometry is traced from Kästner, through his student Gauss, through the generalization of anti-Euclidean geometry by Riemann. This is not to be confused with the interesting, but relatively superficial “non-Euclidean” geometry of a Lobatchevsky and Janos Bolyai. Kästner, the leading German defender of the legacies of both Leibniz and Johann Sebastian Bach against the Eighteenth-century “Enlightenment” reductionists, was also the founder of the German Classic of Lessing, Mendelssohn, and such of their followers as Goethe, Friedrich Schiller, and the Humboldt brothers, in addition to causing the rescue of the works of William Shakespeare from their savage mutilation in the England of Walpole et al.
21. Truth is expressed as action cohering with the essentially infinitesimal quality of the catenary. Scientific progress seeks to approximate that truth. As Leibniz taught, but an enraged Euler denied, it is truth, not mathematical approximations, which runs the universe, e.g., Leonard Euler, Letters to a German Princess, 1761. Hence Euler’s denial of the infinitesimal for calculus, and Euler’s and Lagrange’s obsession with their protests against the reality of the complex domain. Hence, Euler’s accomplice Maupertuis’ fraudulent claim to have discovered a principle of least action.
22. Kepler, op. cit.
23. The principle of least action (as opposed to, for example, shortest distance) points in that direction. With Riemann’s habilitation dissertation, the notion of changes in characteristic values of action becomes a distinct idea.
24. The notion of development within the universe as a universe suggests four possibilities:
- The development within the universe which occurs through mankind’s application of discovered universal principles which have the quality of Platonic powers. This is a scientific certainty.
- The self-development of the universe implicit in the notion of a fixed set of active,“original” physical principles considered as Platonic powers. This is also a certainty, as the presently considered development of a solar system from a “young,” fast-spinning sun implies such development.
- That man, by discovering and adopting the power inhering in such knowledge of a self-developing universe, qualitatively expands and accelerates the self-development of the universe in man’s practiced role as a conscious agent of the Creator.
- The great ontological paradox, that the Creator, as a self-subsisting personality, creates new primary universal principles (powers) within an otherwise self-developing universe. For our purposes here, we limit most of our discussion to the first three of these notions of development of what Vernadsky identified as the Noösphere.
25. For example: Note for later reference, that man’s efficient discovery of a principle associated with abiotic phase-space increases the anti-entropy of the universe by this copying action from the ostensibly abiotic to anti-entropic to the cognitive domain.
26. There is one qualification to be added to that at later point in this report. The efficient addition of the practiced discovery of any universal principle to mankind’s knowledgeable practice, changes the principled character of that phase-space, but, despite that, the fact that a pre-existing principle of the universe is added to human knowledge does not add to the roster of physical principles in the universe as a whole, even though the resulting human activity may change the characteristic anti-entropic efficiency of the universe as a whole.
27. LaRouche, op. cit.
28. Again, the term “power” is used here in the sense of Plato, Leibniz, Gauss, et al., in contrast to the reductionists such as Euler, Lagrange, Cauchy, et al.
29. In follow-up on my initial wrestling against the quackery of Professor Norbert Wiener (most notably, Cybernetics: The Human Use of Human Beings) and John von Neumann (most notably, The Theory of Games and Economic Behavior, The Computer and the Brain), I was confronted by Erwin Schrödinger’s What Is Life? What Schrödinger failed to grasp, is that the physical evidence for a specific principle of life, as distinct from the abiotic domain, precludes any reductionist inference. Schrödinger, to his credit, was a physicist at heart, despite the Machian influence represented by Boltzmann’s work; but, his influence is all the more dangerous to science, simply because he is less implausible than the obviously epistemologically childish Bertrand Russell clones Wiener and von Neumann. See the later discussion here of Vernadsky’s concept of life, for more on this ticklish issue of defining a principle of life as such.
30. This is “anti-Euclidean” in the sense of the use of the term by Gauss’s teacher Abraham Kästner. It has the geometry implied by such early Gauss writings as his 1799 report of the fundamental theorem of algebra, a meaning more amply expressed by Riemann’s 1854 habilitation dissertation.
31. I would define what Vernadsky appropriately terms “noëtic” processes as cognitive in the sense of Plato’s principle of hypothesis. Here, I continue to reference Vernadsky’s use of the term up to the point of this report I have made my own preferences clear. I mean cognition (noësis) in the sense of a Riemannian, anti-Euclidean physical geometry, as Riemann employs “hypothesis.”
32. In Christian theology, for example, there is no knowledge except through the Platonic principle of contradiction. In mathematics, this takes the form of saying that nothing real exists outside the complex domain identified by Gauss, Riemann, et al.
![]()
schiller@schillerinstitute.org
The Schiller Institute
PO BOX 20244
Washington, DC 20041-0244
703-297-8368
Thank you for supporting the Schiller Institute. Your membership and contributions enable us to publish FIDELIO Magazine, and to sponsor concerts, conferences, and other activities which represent critical interventions into the policy making and cultural life of the nation and the world.
Contributions and memberships are not tax-deductible.
VISIT THESE OTHER PAGES:
Home | Search | About | Fidelio | Economy | Strategy | The LaRouche Frameup | Conferences
Links | LaRouche | Music | Join | Books | Concerts | Highlights | Education |
Health | Spanish Pages | Poetry | Dialogue of Cultures
Maps | What's New
© Copyright Schiller Institute, Inc. 2006. All Rights Reserved.
