
Conferencias - Ciencia - Arte - Literatura - Noticias - Unase
Inglés - Inicio
Literatura
Artículos especiales
Pitágoras tiene a un maestro delirando por el éxodo hacia LaRouche

Sky Shields, el autor, hace una demostración con una superficie
mínima helicoidal formada por una película de jabón
Los organizadores del MJL han estado desplegando de manera regular por todos los Estados Unidos y a nivel mundial, tratando de abrir un diálogo sobre el tipo de ideas necesarias para evitar una crisis civilizacional de guerra y depresión. En general lo logramos, pero hemos tenido unas cuantas excepciones notables.
Puesto que hemos puesto de relieve el dominio del teorema de Pitágoras (es decir, entender por qué es verdadero, y no sólo cuál es la fórmula) en nuestro trabajo educativo, los organizadores seguido retan a los estudiantes con los que se topan a producir una prueba. El propósito es demostrar la diferencia entre el mero aprendizaje y el conocimiento verdadero.
A un reportero del periódico Golden Gater de la Universidad Estatal de San Francisco aparentemente lo provocó semejante reto. Hubiéramos preferido que tratara de pensar en el asunto por sí mismo. En cambio, parece que tomó el enfoque contrario, y buscó la opinión de una "autoridad", en este caso el director del Departamento de Matemáticas de la universidad. Los comentarios que citó de este "experto" nos parecieron tan tontos, que tuvimos que echar un vistazo al programa que enseña, mismo que probó ser un ejemplo perfecto del problema que criticamos.
Primero, citemos el informe del periódico universitario:
" `La idea de la fracción perdida que representa el hueco entre el uno y el dos tiene más de 2.500 años de antigüedad, remontándose a Pitágoras', dice el doctor David Meredith, director del Departamento de Matemáticas de la Universidad Estatal de San Francisco, quien dice que una vez perdió a un estudiante por la `secta' de LaRouche. Añade que la enseñanza moderna de las matemáticas alienta a los alumnos a aprender y buscar nuevas verdades por sí mismos, en vez de imitarlas".
El autor de este artículo obtuvo el currículo de la materia de matemáticas del sitio electrónico de la escuela, para descubrir qué enseñan ahí, y por qué Meredith afirma que le permite a los alumnos "buscar nuevas verdades por sí mismos". Esto es del libro Elementary and Intermediate Algebra (Álgebra elemental e intermedia), disponible en la librería de la universidad:
"Un triángulo es un triángulo rectángulo si tiene un ángulo recto de 90°. El lado opuesto al ángulo de 90° se llama hipotenusa. Los otros lados se llaman catetos. En cualquier triángulo rectángulo, si a y b son las longitudes de los catetos y c es la hipotenusa, entonces a2 + b2 = c2 (ver figura 1).
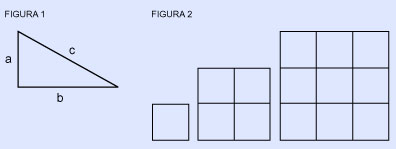
Esto es lo que el autor del libro llama "el teorema de Pitágoras". Ahora bien, ¿qué significa exactamente esa fórmula? Al probarlo en triángulos, sustituyendo las longitudes de los catetos, un estudiante podrá ver que parece "funcionar" en cada caso. Pero, ¿por qué? ¿Porque lo dice el libro?
El teorema de Pitágoras —o lo que queda de él como lo enseñan aquí— tiene, al igual que otras técnicas algebraicas, tales como "completar el cuadrado", la formula cuadrática, etc., el mismo significado para la mayoría de los modernos maestros de matemáticas, y para las víctimas de su malicioso entrenamiento de perros de exhibición, tal como lo que el muñeco con alfileres es para la sacerdotisa vudú: un talismán místico a usar del mismo modo desesperado demostrado por Euler, LaGrange y Jean Le Rond d'Alembert, según el recuento de Gauss de sus intentos por probar, usando la manipulación de símbolos aprendidos, el teorema fundamental del álgebra. La verdadera álgebra (al–yabr) de Al–Khwarizmi, que esta formulación del libro de texto oscurece, cobra una forma completmente diferente, incluso opuesta.
El verdadero teorema de Pitágoras
Primero, ¿qué significa elevar un número al "cuadrado"? ¿Es sólo el acto de multiplicar un número dado por sí mismo? Si es así, ¿qué tiene esto que ver con las longitudes de los lados de un triángulo rectángulo?
La respuesta a esto puede encontrarse en una investigación general de las propiedades de los cuadrados. Los lectores familiarizados con el diálogo del Menón de Platón, o que hayan intentado resolver el problema de doblar el cuadrado, saben que esto no puede hacerse simplemente doblando la longitud de uno de los lados. Esta acción resulta en un cuadrado cuatro veces mas grande que el original; el triplicar la longitud del lado resulta en un cuadrado nueve veces más grande, y así sucesivamente (ver figura 2).
Uno puede investigar la relación entre la longitud de una línea y el cuadrado construido sobre ella. Es una representación de esta relación físico–geométrica, que más tarde se conoce como "elevar un número al cuadrado" (Arquitas, y luego Gauss, demostraron que este era un caso especial de un concepto físico–geométrico más general de poderes).
Ahora, regresando a nuestro triángulo, "a cuadrada" parecería significar el cuadrado construido sobre la longitud a. Nuestro teorema se vería entonces un poco como la imagen de la figura 3. Pero ahora tenemos un nuevo problema: ¿cómo agregar un cuadrado a otro, y seguir teniendo un cuadrado? El lector debe intentar diferentes métodos para esto antes de ver la solución que presentaremos aquí.
Como demostración (esta es sólo una de varias posibles): observando nuestro dibujo, vemos varios triángulos implícitos más, cada uno igual a nuestro triángulo original. Dibújalos todos (ver figura 4). Un examen minucioso revelará dos cuadrados idénticos en la construcción, cada uno con un lado de longitud combinada a + b, y con cuatro de los triángulos originales dentro como parte de su área (uno de estos cuadrados idénticos aparece, por sí mismo, en la figura 5).
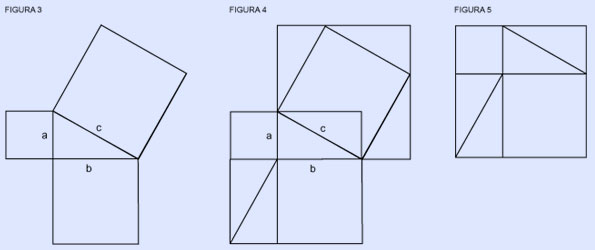
Si removemos la misma área de cada uno de los dos cuadrados idénticos —en este caso los cuatro triángulos— debiéramos obtener la misma área restante. Pero, en el primer caso, tenemos dos cuadrados que sobran: el cuadrado a y el cuadrado b. En el otro caso, tenemos sólo uno, el cuadrado c. Pero, debido a nuestra construcción, ¡estas áreas deben ser iguales! Esto es, a al cuadrado más b al cuadrado debe ser igual a c al cuadrado.
"¡Pero no puedes esperar que la gente pase por todo esto! ¡Tomaría demasiado tiempo!", sería la queja típica de cualquier profesor de las "nuevas matemáticas", o quizás de algún joven que aspire a ascender socialmente y a integrarse a un partido político de pacotilla ("¡Esto no me ayudará a conseguir un trabajo bien remunerado! Yo sólo quiero hacer amistades e influencias".).
Pero lo cierto es que, precisamente por el hecho de que la mayoría de la gente que consideramos nuestra dirigencia política e intelectual en el mundo hoy día no ha trabajado en problemas como este, ahora estamos en la crisis en la que estamos. Hemos llegado al final de un sistema, donde todas la reglas aceptadas de economía, relaciones sociales, ciencia y matemáticas ya no funcionan. Y sólo si hay un movimiento en el mundo hoy, centrado en torno a redescubrir el método por el cual se hacen los descubrimientos (y no sólo se consumen sus derivados), seremos capaces de buscar las nuevas ideas necesarias para salir de este desastre.
Artículos relacionados:
La Juventud Larouchista y la ciencia
Por qué todo el mundo debe entender a Gauss
schiller@schillerinstitute.org
PO BOX 20244 Washington, DC 20041-0244
703-297-8368
Copyright Schiller Institute, Inc. 2001. Todos los derechos reservados