
Conferencias - Ciencia - Arte - Literatura - Noticias - Unase
Inglés - Inicio
Ciencia y cultura
Artículos especiales
Volviendo visible lo invisible
El teorema fundamental del álgebra

Carl Friedrich Gauss
por Bruce Director
1. La declaración de independencia de Gauss
En septiembre de 1798, después de tres años de estudios, el gran matemático Carl Friedrich Gauss, entonces de 21 años de edad, abandonó la Universidad de Gotinga sin recibir un diploma. Regresó a su ciudad natal, Braunschweig, para empezar a escribir su Disquisitiones Arithmeticae, y, sin perspectivas de empleo, abrigaba la esperanza de seguir recibiendo su estipendio de estudiante, sin la seguridad de que su benefactor, Carl Wilhelm Ferdinand, duque de Braunschweig, se lo daría. Después de vivir de fiado varios meses, el Duque le dejó saber que su estipendio continuaría, con tal de que Gauss obtuviera su título de doctorado en filosofía, una tarea que Gauss consideraba una distracción, y que deseaba posponer.
No obstante, Gauss aprovechó la oportunidad de hacer una virtual declaración de independencia del asfixiante mundo de las matemáticas deductivas, en la forma de una tesis escrita que envió al profesorado de la Universidad de Helmstedt, sobre una nueva prueba del teorema fundamental del álgebra. En cosa de meses, recibió su doctorado sin siquiera tener que presentarse para un examen oral.
Describiendo su intención a su ex compañero de clase, Wolfgang Bolyai, Gauss escribió: "El título [teorema fundamental] indica de forma categórica el propósito del ensayo; sin embargo, sólo un tercio del mismo se usa para este propósito; el resto contiene principalmente la historia y una crítica del trabajo de otros matemáticos (a saber, d'Alembert, Bougainville, Euler, de Foncenex, Lagrange y los enciclopedistas. . . quienes, sin embargo, tal vez no estarán muy contentos) sobre el mismo tema, además de muchos y variados comentarios sobre la superficialidad que predomina tanto en nuestras matemáticas actuales".
En esencia, Gauss defendió y amplió un principio que se remonta a Platón, en el que sólo la acción física define nuestra noción de magnitud, y no los supuestos arbitrarios. Como Platón, Gauss reconoció que no bastaría simplemente con declarar su descubrimiento, a menos que lo combinara con un ataque polémico contra las falsedades aristotélicas que se habían vuelto tan populares entre sus contemporáneos.
Viendo su disertación 50 años después, Gauss dijo: "La demostración se presenta tomando expresiones prestadas de la geometría de posición; porque de este modo se alcanza la mayor agudeza y simplicidad. Fundamentalmente, el contenido esencial de todo el argumento pertenece a un dominio superior, independiente del espacio [es decir, antieuclidiano], en el que los conceptos generales de magnitud se investigan como combinaciones de magnitudes conectadas por continuidad: un dominio que, al presente, se ha desarrollado poco, y en el que uno no puede moverse sin tomar prestado el lenguaje de las imágenes espaciales".
Mi intención es ofrecer un bosquejo resumido de la historia de esta idea, y de su desarrollo por Gauss. No puede ser exhaustivo. Más bien, busco trazar los pasos que deberían formar la base de diálogos pedagógicos orales, que ya están en marcha en varios lugares.[1]
Magnitud múltiplemente extendida
Los círculos asociados con Platón ya habían desarrollado un concepto físico cabal de magnitud, que se expresa más explícitamente en los diálogos Menón, Teetetes y Timeo. Platón y los suyos demostraron este concepto de manera pedagógica por medio de las paradojas que surgen cuando se considera la singularidad de los cinco sólidos regulares, y los problemas relacionados de doblar de una línea, un cuadrado y un cubo. Como Platón subrayó, cada especie de acción generaba una magnitud de especie diferente. Él denominó a tales especies con la palabra griega dúnamis (raíz de la palabra dínamo), término que mejor se puede vertir al español como poder.[2] El significado de dúnamis es similar al uso que hace Godofredo G. Leibniz de la palabra alemana kraft.
Esto es, que una magnitud lineal tiene el "poder" de doblar una línea, mientras que sólo una magnitud de una especie diferente tiene el "poder" de doblar un cuadrado, y aun una especie diferente tiene el "poder" de doblar un cubo [ver figuras 1(a)–(c)]. En el lenguaje de Bernhard Riemann, a estas magnitudes se les llama, de manera respectiva: simplemente, doblemente y triplemente extendidas. El grupo de Platón destacó que las magnitudes de menor extensión carecían del potencial para generar magnitudes de extensión superior, creando, conceptualmente, una sucesión de "poderes superiores".
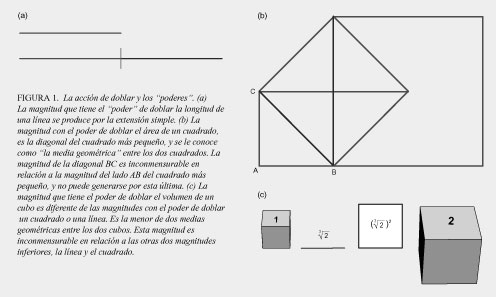
No pensemos aquí en el uso deductivo del término "dimensión". Aunque "dimensión" es una palabra perfectamente correcta, en la usanza moderna a menudo se le asocia con la idea kantiana del espacio euclidiano formal, en la cual se considera al espacio como una combinación de tres dimensiones independientes, simplemente extendidas.
Pensemos, mejor, en "extensión física". Una línea se produce por medio de una acción física de extensión simple. Puede que a una superficie la confinen líneas, pero no está hecha de líneas; más bien, una superficie está, de manera irreducible, doblemente extendida. Asimismo, a un volumen pueden confinarlo superficies, a su vez confinadas por líneas, empero, de forma irreducible, está triplemente extendido.
Así, una unidad de línea, de cuadrado o de cubo puede caracterizarse por el número uno, pero cada uno es de una especie diferente de poder.
El grupo de Platón también subrayó que esta sucesión de magnitudes de poderes superiores era generada por una sucesión de tipos de acción diferentes. Específicamente, la acción lineal la producía una magnitud simplemente extendida, la acción circular una doblemente extendida, y la acción circular extendida una triplemente extendida, como las acciones de rotación que generan un cono, un cilindro o un toro. Platón presenta esto de forma pedagógica en el diálogo Menón, con respecto a las magnitudes doblemente extendidas, y en Timeo, respecto a la singularidad de los cinco sólidos regulares y el problema de doblar el cubo. Arquitas, colaborador de Platón, demostró que la magnitud que dobla a un cubo no se genera por la acción circular, sino por la acción circular extendida, es decir, las secciones cónicas [ver figuras 2(a) y 2(b)].

Le correspondió a Apolonio de Perga (262–200 a.C.) presentar una exposición completa de la generación de magnitudes de poderes superiores en su trabajo sobre las Cónicas. Apolonio investigó de manera exhaustiva la generación de magnitudes doble y triplemente extendidas, a las que distinguió entre lugares geométricos planos (el círculo/la línea), y sólidos (la elipse, la parábola, la hipérbola).
Como Abraham Gotthelf Kästner indica en su Historia de las matemáticas (1797), la investigación de las relaciones entre poderes superiores dio paso a lo que se conocería con la palabra de origen árabe, álgebra; y a partir de Leibniz (1644–1716) en adelante, como análisis. Aquí, se investigó la relación de magnitudes del segundo poder (los cuadrados), y del tercer poder (los cubos) en la forma de ecuaciones algebraicas cuadráticas y cúbicas, respectivamente. Entretanto, las ecuaciones superiores del tercer grado cobraron una importancia formal, pero carecían del referente físico visible de las cuadráticas y cúbicas.
Girolamo Cardano (1501–1576) y, posteriormente, Leibniz, mostraron que había un "hueco" en toda forma de ecuación algebraica, como mostraba la aparición de raíces cuadradas de números negativos como soluciones a ciertas ecuaciones. Escudriñando este "hueco", Leibniz reconoció que el álgebra no podía enseñar nada sobre la física, pero que, más bien, un principio físico general subsume a todas las ecuaciones algebraicas, de cualquier poder.
Leibniz, en una carta que escribió en 1675 a Christian Huyghens (1629–1695) sobre las raíces cuadradas de los números negativos, añadió que había inventado una máquina que producía exactamente la acción requerida por este principio físico general:
"Parece que después de este instrumento, no puede desearse casi nada más para el uso que el álgebra puede o podría tener en la mecánica y en la práctica. Es creíble que este era el objetivo de la geometría de los antiguos (al menos de Apolonio) y el propósito de los lugares geométricos, que él introdujo, porque reconoció que unas cuantas líneas determinan instantáneamente lo que largos cálculos numéricos sólo podrían lograr después de un arduo trabajo capaz de desalentar al más pintado".
Aunque determinó la acción física que generaba una sucesión de poderes superiores, Leibniz dejó abierta la cuestión de cuál era la acción física que producía las raíces cuadradas de los números negativos.
La prueba de Gauss del teorema fundamental
Para cuando Gauss abandonó Gotinga, ya había desarrollado un concepto de realidad física de las raíces cuadradas de los números negativos, al que llamó: números complejos. Gauss, adoptando el método de la metáfora de la caverna, de la República de Platón, comprendió que sus números complejos eran sólo sombras que reflejaban un complejo de acciones físicas (la acción actuando sobre la acción). Esta acción compleja reflejaba un poder superior a la acción triplemente extendida que caracteriza a la multiplicidad del espacio visible.
La contribución singular de Gauss fue idear una metáfora que significara estas formas superiores de acción física, de modo que pudieran representarse, por medio de sus reflejos, en el dominio visible.
En su disertación de 1799, Gauss optó de manera brillante por desarrollar su metáfora de forma polémica, en el flanco más vulnerable de las ecuaciones algebraicas de sus oponentes. Al igual que Leibniz, Gauss rechazó la perspectiva deductiva en la investigación de las ecuaciones algebraicas en sus propios términos, insistiendo en que era la acción física la que determinaba las características de las ecuaciones.
Un ejemplo simple nos ayudará a ilustrar la cuestión. Piensa en el significado físico de la ecuación x2=4. Sabemos que x se refiere al lado de un cuadrado cuya área es 4. Así, 2 es una solución a la ecuación. Ahora, piensa en el significado físico de la ecuación x2=−4. Desde un punto de vista deductivo formal, esta ecuación se refiere al lado de un cuadrado cuya área es −4. Empero, ¿cómo un cuadrado puede tener un área (negativa) de −4? Formalmente, la segunda ecuación puede resolverse introduciendo el número 2 √−1, o 2i (donde i denota √−1), que, cuando se eleva al cuadrado, es igual a −4. Pero la interrogante sigue, ¿cuál es el significado físico de √−1?
Una respuesta sería decir que √−1 no tiene significado físico, y por tanto la ecuación x2=−4 no tiene solución. A esto, Euler y Lagrange le añadieron la sofistería, muy ridiculizada por Gauss en su disertación, de que la ecuación x2=−4 tiene una solución, ¡pero que esa solución es imposible!
Gauss demostró el significado físico de √−1, no en el dominio visible de los cuadrados, sino en el dominio cognoscitivo del principio de cuadrar.
Esto puede ilustrarse pedagógicamente si trazas un cuadrado, cuya área llamaremos 1. Luego, traza una diagonal A de ese cuadrado, y traza un nuevo cuadrado usando esa diagonal como lado. El área del nuevo cuadrado será 2. Ahora, repite esta acción para generar un cuadrado cuya área sea 4 (ver figura 3).
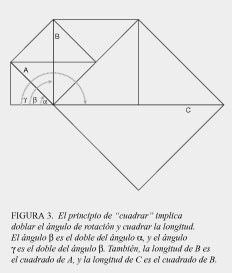
¿Cuál es el principio de cuadrar que ilustra esto? La acción que generó la magnitud que produjo el cuadrado cuya área es 2, fue una rotación de 45° y una extensión de la longitud de 1, el lado del primer cuadrado, a √2, su diagonal, que se convirtió en el lado del siguiente cuadrado. Para producir el cuadrado cuya área es 4, la rotación de 45° se dobló a 90°, y la extensión se cuadró para convertirse en 2. Repite este proceso varias veces para ilustrar que el principio de cuadrar puede considerarse como la acción física combinada de doblar una rotación y cuadrar una longitud. La raíz cuadrada es simplemente la acción inversa, ésto es, dividir a la mitad el ángulo de rotación y disminuir la longitud por la raíz cuadrada.
Ahora, traza un círculo N y un diámetro, y aplica esta acción física de cuadrar a cada punto sobre el círculo. Esto es, toma cualquier punto sobre la circunferencia del círculo (el punto z en la figura). Traza el radio que conecta a ese punto con el centro del círculo. Ese radio forma un ángulo con el diámetro que trazaste. Para "cuadrar" ese punto, dobla el ángulo α entre el radio y el diámetro para formar el ángulo β, y cuadra la longitud. Repite esta acción con varios puntos. Pronto podrás observar que todos los puntos del primer círculo se proyectan como puntos sobre un círculo concéntrico más grande, cuyo radio es el cuadrado del círculo original. Pero, esto se vuelve más y más interesante. Puesto que doblas el ángulo cada vez que cuadras un punto, el círculo original se proyectará en el círculo "cuadrado" dos veces (ver figura 4)
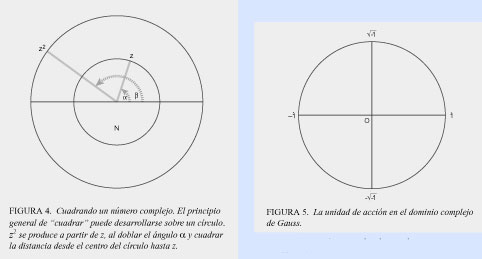
Hay un ejemplo físico que ilustra este proceso. Toma un imán y mueve una brújula a su alrededor. Mientras la brújula se mueve del polo norte al sur del imán (180°), la aguja de la brújula completará una revolución (360°). Y en tanto se mueve del polo sur de vuelta al norte, la aguja completará otra revolución. En efecto, ¡el imán "cuadra" la brújula!
Gauss asoció sus números complejos con este tipo de acción física compuesta (rotación combinada con extensión). Los hizo visibles, metafóricamente, como una acción espiral proyectada sobre una superficie. Cada punto sobre esa superficie representa un número complejo. Cada número expresa una combinación única de rotación y extensión. El punto de origen de la acción en última instancia se refiere a la singularidad física, como la del punto inferior de la catenaria, o los polos de rotación de la Tierra, o el centro del imán.
En el ejemplo anterior, considera al círculo original como una unidad de círculo en el dominio complejo. El centro del círculo es el origen, indicado por O, los extremos del diámetro los denotan 1 y −1. La raíz cuadrada de −1 se encuentra al dividir en dos la rotación entre 1 y −1, y reduciendo el radio por la raíz cuadrada. Piensa con cuidado y verás que los puntos sobre la circunferencia que se encuentran en medio de 1 y −1 representan a √−1 y −√−1 (ver figura 5).
Gauss demostró que todos los poderes algebraicos, de cualquier grado, cuando se proyectan en su dominio complejo, podrían representarse por una acción parecida a la que acabamos de demostrar para la acción de cuadrar. Por ejemplo, la acción de cubicar un número complejo se logra triplicando el ángulo de rotación y cubicando la longitud. Esto hace que el círculo original se proyecte tres veces en un círculo cuyo radio es el cubo del círculo original. La acción asociada con el poder bicuadrático (de cuarto grado) implica cuadruplicar el ángulo de rotación y cuadrar el cuadrado de la longitud. Esto hará que el círculo original se proyecte cuatro veces en un círculo cuyo radio aumenta por el cuadrado del cuadrado, y así sucesivamente para todos los poderes superiores.
Así, aunque las multiplicidades de acción asociadas a estos poderes superiores existen fuera de la multiplicidad triplemente extendida del espacio visible, Gauss develó, en su dominio complejo, la característica de acción que las produce.
2. Volviendo visible lo invisible
Cuando Carl Friederich Gauss le escribió a Wolfgang Bolyai en 1798, criticando la `superficialidad' de las matemáticas de la época, hablaba literalmente, y no sólo de su época, sino también de la nuestra. Entonces, como ahora, se había hecho popular entre los académicos desdeñar, e incluso ridiculizar, cualquier esfuerzo por descubrir principios físicos universales, limitando el campo de la investigación científica a la tarea aparentemente más práctica de describir sólo lo que es visible en la superficie. Irónicamente, como Gauss demostró en su disertación doctoral de 1799 sobre el teorema fundamental del álgebra, lo que está en la superficie sólo se revela si uno sabe lo que lo subyace.
El método de Gauss era uno antiguo, que hizo famoso la metáfora de la caverna, de Platón, y que cobrara nueva potencia con la aplicación de Johannes Kepler del método de la Docta ignorancia de Nicolás de Cusa. Para ellos, la tarea del científico era hacer visibles los principios físicos subyacentes que no pueden observarse directamente; lo invisible que guía a lo visible.
Para ilustrar esto, tomemos como ejemplo el descubrimiento de Fermat del principio de que la luz refractada sigue la trayectoria de tiempo mínimo, en vez de la de menor distancia que sigue la luz reflejada. El principio de menor distancia se encuentra en la superficie, y puede demostrarse en el dominio de lo visible. Por su parte, el principio del tiempo mínimo existe "detrás", por así decirlo, de lo visible, y puede verse sólo en la mente. Reflexionando un poco, es claro que el principio del tiempo mínimo siempre estuvo ahí, controlando, invisiblemente, al principio de menor distancia. En los términos de referencia de Platón, el principio del menor tiempo es de un "poder superior" que el de menor distancia.
El descubrimiento de Fermat es un punto de referencia útil para comprender el concepto del dominio complejo de Gauss. Como Gauss mismo puntualizó inequívocamente, el dominio complejo no se refiere al concepto superficial, formal, de los números imaginarios o "imposibles" que desarrolló Euler, y que enseñan los "expertos" desde entonces. Más bien, el concepto de Gauss del dominio complejo, como el principio del tiempo mínimo de Fermat, trae a la superficie un principio que siempre estuvo ahí, pero escondido a la vista.
Lo algebraico y lo trascendental
Como subrayó Gauss en la revisión de su disertación de 1799, el concepto del dominio complejo es un "dominio superior", independiente de todos los conceptos a priori del espacio. No obstante, es un dominio "en el que uno no puede moverse sin tomar prestado el lenguaje de las imágenes espaciales".
Su objetivo, como el de Leibniz, era encontrar un principio general que caracterizara lo que llegó a conocerse como magnitudes "algebraicas". Estas magnitudes, inicialmente relacionadas con la extensión de líneas, cuadrados y cubos, están comprendidas bajo el concepto de dúnamis, o poder, de Platón.
Leibniz había demostrado que, en tanto que el dominio de todas las magnitudes "algebraicas" consistía en una sucesión de poderes superiores, este dominio algebraico en su totalidad lo dominaba un poder aun superior, que llamó "trascendental". La relación entre el dominio inferior de las magnitudes algebraicas, y el superior, no algebraico, de las magnitudes trascendentales, se refleja en el descubrimiento de Jakob Bernoulli de la espiral equiangular (ver figura 6)
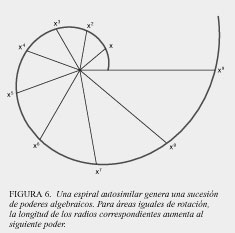
Leibniz demostró más tarde, junto con el hermano de Jakob, Johann Bernoulli, que este dominio trascendental superior no existe como un principio puramente abstracto, sino que se origina en la acción física de una cadena suspendida, cuya forma geométrica Christiaan Huyghens llamó una catenaria (ver figura 7). Así, el propio universo físico demuestra que las magnitudes "algebraicas" relacionadas con la extensión no se generan por ésta, sino a partir de un principio físico que existe más allá de la simple extensión, en el dominio trascendental, superior.
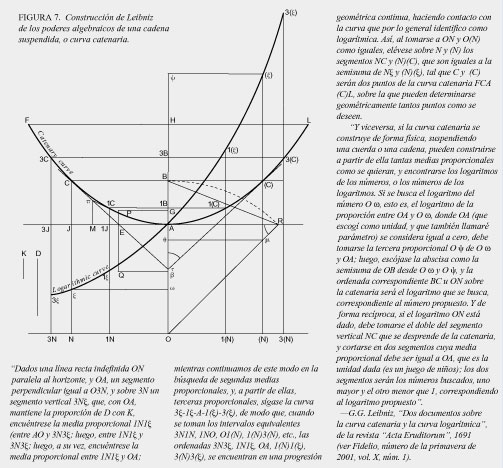
En sus pruebas del teorema fundamental del álgebra, Gauss demostró que, aunque este principio físico trascendental no estaba en el dominio de lo visible, de cualquier modo "proyecta una sombra" que puede hacerse visible en lo que él llamó el dominio complejo.
Como se indicó en la primera parte, se descubrió un principio general para magnitudes algebraicas viendo a través del "hueco" que representan las raíces cuadradas de los números negativos. Estas raíces cuadradas aparecían como soluciones a ecuaciones algebraicas, pero carecían de significado físico aparente alguno. Por ejemplo, en la ecuación algebraica x2=4, x es el lado de un cuadrado cuya área es 4; mientras que, en la ecuación x2=−4, x es el lado de un cuadrado de área −4, algo aparentemente imposible.
En el primer caso, es fácil ver que una línea cuya longitud es 2 sería el lado de un cuadrado de área 4; sin embargo, desde el punto de vista algebraico, una línea cuya longitud es −2, también produce un cuadrado de área 4. A primera vista, una línea de longitud −2 parece tan imposible como un cuadrado de área −4; sin embargo, si dibujas un cuadrado de área 2, verás que tiene dos diagonales, ambas con el poder de producir un nuevo cuadrado de área 4. Estas dos magnitudes sólo se diferencian la una de la otra por su dirección, así que una se designa como 2 y la otra como −2.
Ahora, extiende la investigación al cubo. En la ecuación algebraica X3=8, parece haber sólo un número, el 2, que satisface la ecuación, y este número es la arista de un cubo cuyo volumen es 8. Esta parece ser la única solución, puesto que (−2)(−2)(−2)=−8, es otra aparente imposibilidad. La anomalía de que hay dos soluciones en el caso de una ecuación cuadrática, parece desaparecer en el caso del cubo, para el que parece haber sólo una solución.
Trisectando un ángulo
Pero, no tan rápido. Mira otro problema geométrico que, al representarse en términos algebraicos, presenta la misma paradoja: la trisección de un ángulo arbitrario. Igual que al doblar el volumen del cubo, los geómetras griegos tampoco pudieron encontrar una media proporcional para trisectar un ángulo arbitrario, desde el propio principio de acción circular. Los diversos métodos descubiertos (por Arquímedes, Eratóstenes y otros) para encontrar un principio general de trisectar un ángulo, eran parecidos a aquellos que descubrieron los colaboradores de Platón para doblar el cubo. Esto es, esta magnitud no puede construirse usando sólo un círculo y una línea recta, sino que requería emplear la acción circular extendida, tal como la acción cónica. Pero trisectar un ángulo arbitrario presenta otro tipo de paradoja, que no es tan patente en el problema de doblar el cubo. Para ilustrar esto, realiza el siguiente experimento:
Traza un círculo (ver figura 8). Para hacer más clara la ilustración, marca un ángulo de 60°. Es claro que un ángulo de 20° trisectará este ángulo. Ahora, súmale una revolución completa al ángulo de 60°, formando un ángulo de 420°. Pareciera que estos dos ángulos, 60° y 420°, en esencia son lo mismo, pero cuando divides 420° entre tres, obtienes un ángulo de 140°. Añade otra rotación de 360°, y llegamos a un ángulo de 780°, que pareciera ser exactamente lo mismo que los ángulos de 60° y 420°. Sin embargo, cuando dividimos 780° entre tres obtenemos un ángulo de 260°. Continua haciendo esto y verás que se repite la misma pauta una y otra vez.
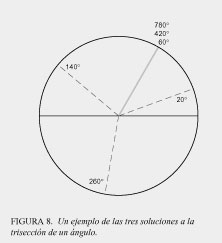
Visto como una "certeza sensorial", el ángulo de 20° es el único que trisecta al de 60°. Sin embargo, cuando uno ve más allá de la certeza sensorial, es claro que hay tres ángulos que "resuelven" el problema.
Esto ilustra otro "hueco" en la determinación algebraica de magnitud. En el caso de las ecuaciones cuadráticas, pareciera haber dos soluciones para cada problema. En algunos casos, como x2=4, esas soluciones parecen tener una existencia visible; en tanto que para x2=−4, hay 2 soluciones, 2√−1 y −2√−1, las cuales, ambas, parecen ser "imaginarias", sin significado físico. En el caso de las ecuaciones cúbicas, a veces hay tres soluciones visibles, como en el caso de la trisección de un ángulo; pero al doblar el cubo, pareciera haber sólo una solución visible y dos "imaginarias": −1−(√3)(√−1); y −1 + (√3)(√−1).
Las ecuaciones bicuadráticas, como x4=16, que parecieran no tener significado físico en sí mismas, tienen 4 soluciones, 2 "reales" (2 y −2) y dos "imaginarias" (2√−1 y −2√−1).
Todo se torna más confuso con magnitudes algebraicas de poderes aún superiores. Esta anomalía establece la interrogante que Gauss resolvió en su prueba de lo que llamó el "teorema fundamental" del álgebra: ¿Cuántas soluciones existen para cualquier ecuación algebraica dada?
Los matemáticos de razonamiento "superficial" en la época de Gauss, como Euler, Lagrange y D'Alembert, respondieron con la perspectiva superficial de que una ecuación algebraica tendrá tantas soluciones como potencias tenga, aunque algunas de estas soluciones sean "imposibles", como la raíz cuadrada de los números negativos. (Este argumento sofista es como decir: "Hay una diferencia entre el hombre y las bestias, pero no significa nada".)
Las sombras de las sombras: el dominio complejo
En su disertación de 1799, Gauss polemizó y puso al descubierto este fraude como la sofistería que era: "Si alguien dijera que un triángulo rectángulo equilátero rectilíneo es imposible, nadie lo negaría. Pero si pretendiese proponer semejante triángulo imposible como una nueva especie de triángulos y aplicarle otras cualidades de los triángulos, ¿podría alguien contener la risa? Eso sería un juego de palabras, o más bien, emplearlas mal".
Para Gauss, ninguna magnitud era admisible, a menos que se demostrara su principio generador. Para magnitudes relacionadas con las raíces cuadradas de los números negativos, ese principio era la acción física compleja de la rotación combinada con extensión. Gauss llamó a las magnitudes generadas por esta acción compleja, "números complejos". Cada número complejo denotaba cierta cantidad de acción de rotación y de extensión combinadas.
La unidad de acción en el dominio complejo de Gauss es un círculo, que es una rotación con una extensión de uno (unidad de longitud). En este dominio, el número 1 significa una rotación completa; −1, media rotación; √−1, un cuarto de rotación; y −√−1, tres cuartos de rotación (ver figura 5).
Estas "sombras de las sombras", como él las llamó, sólo eran un reflejo visible de un tipo de acción todavía superior, independiente de todos los conceptos visibles del espacio. Estas formas superiores de acción, aunque invisibles, empero podían ponerse de manifiesto como una proyección sobre una superficie.
La perspectiva de Gauss es congruente con la que empleaban los colaboradores de la academia de Platón. En la antigua Grecia, la palabra para superficie, epiphaneia (raíz de la palabra "epifanía" en español), puede interpretarse como "aquello sobre lo cual algo se hace visible".
Desde esta óptica, Gauss demostró en su disertación de 1799, que el principio fundamental para generar cualquier ecuación algebraica, sin importar de qué poder, puede manifestarse, "epifanizarse", por así decirlo, como una superficie en el dominio complejo. Estas superficies eran representaciones visibles, no de lo que producían los poderes —como en los casos de las líneas, los cuadrados y los cubos—, sino del principio que producía esos poderes.
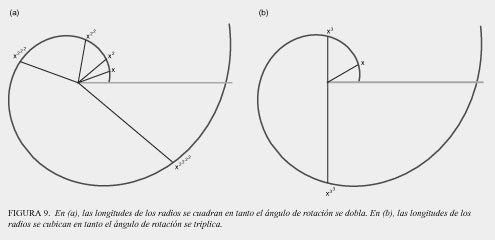
Para construir estas superficies, Gauss salió de la simple representación visible de los poderes —como los cuadrados y cubos— al buscar una forma más general de poderes, como la que se aprecia en la espiral equiangular (ver figura 9). Aquí, la generación de un poder corresponde a la extensión que produce un cambio angular. Por ejemplo, la generación de poderes cuadráticos corresponde a la extensión que resulta de doblar el ángulo de rotación, dentro de la espiral (ver figura 9a); y la generación de poderes cúbicos corresponde a la extensión que resulta de triplicar el ángulo de rotación, dentro de esa espiral (ver figura 9b). Así, es el principio de cuadrar el que produce magnitudes cuadradas, y el principio de cubicar el que produce las cúbicas.
En la figura 10, el número complejo z se "cuadra" cuando el ángulo de rotación se dobla de x a 2x y la longitud se cuadra de A a A2. Al hacer esto, el círculo más pequeño se proyecta dos veces sobre el círculo "cuadrado", más grande, como mostramos en la primera parte. En la figura 11, se ilustra el mismo principio con respecto a cubicar. Aquí, el ángulo x se triplica a 3x, y la longitud A se cubica a A3. En este caso, el círculo más pequeño se proyectará tres veces sobre el círculo "cubicado", más grande. Y así para poderes superiores. En el cuarto poder, el círculo más pequeño se proyectará cuatro veces sobre el más grande; el quinto poder, cinco veces; y así sucesivamente.
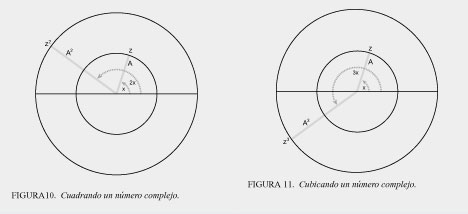
Esto muestra un principio general que determina todos los poderes algebraicos. Desde esta perspectiva, la misma acción refleja a todos los poderes. Lo único que cambia con cada poder es el número de veces que ocurre la acción. Así, cada poder se distingue de los demás, no por una magnitud particular, sino por una característica topológica.
En su disertación doctoral, Gauss usó este principio para generar superficies que expresaran de una manera aún más fundamental la característica esencial de los poderes. Cada rotación y extensión producía un triángulo rectángulo característico. El cateto vertical de ese triángulo es el seno, y el horizontal el coseno (ver figura 12).
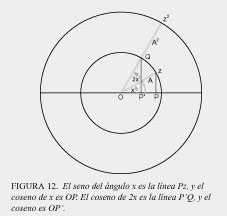
Hay una relación cíclica entre el seno y el coseno que es una función del ángulo de rotación. Cuando el ángulo es 0, el seno es 0 y el coseno es 1. Cuando el ángulo es de 90°, el seno es 1 y el coseno es 0. Si uno sigue esta relación para una rotación completa, el seno va de 0, a 1, a 0, a −1, y de vuelta a 0; mientras que el coseno va de 1, a 0, a −1, a 0, y de vuelta a 1 (ver figura 13).
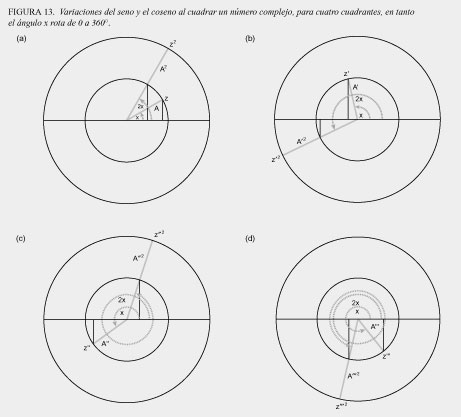
En la figura 13, en tanto z se mueve de 0 a 90°, el seno del ángulo varía de 0 a 1; pero al mismo tiempo, el ángulo para z2 va de 0 a 180°, y el seno de z2 varía de 0 a 1, y de vuelta a 0. Entonces, mientras z se mueve de 90 a 180°, el seno varía de 1 a 0 otra vez, pero el ángulo para z2 ha pasado de 180 a 360°, y su seno ha variado de 0, a −1, a 0. Así, en media rotación de z, el seno de z2 ha variado de 0, a 1, a 0, a −1, a 0.
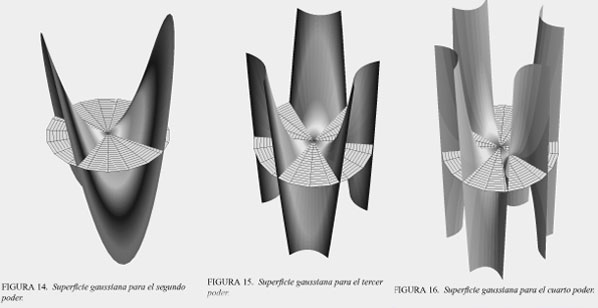
En su disertación doctoral, Gauss representó este complejo de acciones como una superficie (ver figuras 14, 15 y 16). Cada punto sobre la superficie se determina de modo tal, que su altura sobre el plano es igual a la distancia desde el centro por el seno del ángulo de rotación, mientras ese ángulo aumenta por efecto del poder. En otras palabras, el poder de cualquier punto en el plano lo representa la altura de la superficie por sobre ese punto. Así, mientras los números sobre el plano se alejan del centro, la superficie crece más acorde al poder. Al mismo tiempo, al rotar los números en torno al centro, el seno pasará de positivo a negativo. Dado que los números sobre la superficie son los poderes de los números sobre el plano, el número de veces que el seno cambiará de positivo a negativo, dependerá de qué tanto multiplique el poder al ángulo (el doble para poderes cuadrados, el triple para los cúbicos, etc.). Por tanto, cada superficie tendrá tantas "jorobas" como la ecuación tenga dimensiones. Por consiguiente, una ecuación cuadrática tendrá dos "jorobas" para arriba y dos "jorobas" para abajo (ver figura 14). Una ecuación cúbica tendrá tres "jorobas" para arriba y tres para abajo (ver figura 15). Una ecuación de cuarto grado tendrá cuatro "jorobas" en cada dirección (ver figura 16); y así sucesivamente.
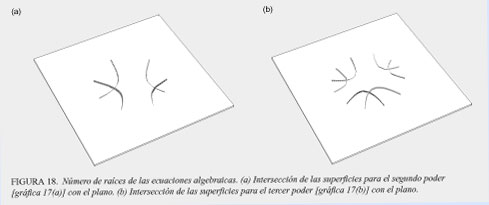
Gauss especificó la construcción de 2 superficies para cada ecuación algebraica, una basada en las variaciones del seno y la otra en las del coseno (ver figura 17) Cada una de estas superficies determinará curvas definidas en donde intersecan con el plano (ver figura 18). El número de curvas dependerá del número de "jorobas", que a su vez depende del poder más alto.
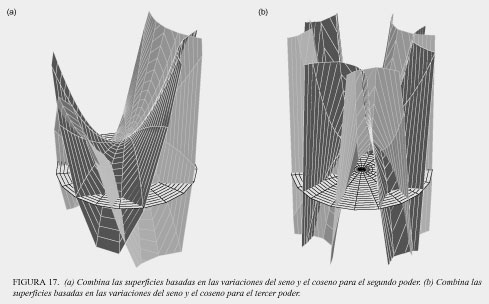
Dado que las superficies del seno y el coseno se rotan 90° en relación el uno del otro, las curvas sobre el plano intersecarán unas a otras, y el número de intersecciones corresponderá al número de poderes. Si se considera al plano como cero, estas intersecciones corresponderán a las soluciones, o "raíces" de la ecuación. Esto comprueba que una ecuación algebraica tiene tantas raíces como su poder más alto (ver figura 18).
El principio de los poderes
Retrocede un poco y observa este trabajo. Estas superficies se generaron, no de cuadrados o cubos visibles, sino del principio general de cuadrar, cubicar y de los poderes superiores. Representan, metafóricamente, un principio que se manifiesta de forma física, pero que no puede verse. Al proyectar este principio —la forma general de los poderes de Platón— sobre estas superficies complejas, Gauss ha hecho visible lo invisible, e inteligible aquello incomprensible en el mundo superficial del formalismo algebraico.
El esfuerzo por hacer inteligibles las implicaciones del dominio complejo fue un asunto clave para Gauss a lo largo de su vida. En una carta dirigida a su amigo Hansen el 11 de diciembre de 1825, Gauss dijo:
"Estas investigaciones llevan profundamente a muchas otras, incluso diría, a la Metafísica de la teoría del espacio; y es sólo con gran dificultad que puedo desprenderme de los resultados que brotan de ellas, como, por ejemplo, la verdadera metafísica de los número negativos y los complejos. El verdadero sentido de la raíz cuadrada de −1 está siempre vivo en mi mente, pero es muy difícil expresarlo con palabras, y sólo logro ofrecer una imagen vaga que flota en el aire".
Fue de aquí de donde partió Bernhard Riemann.
(Traducción de Carlos Cota Moreno y Juan José Mena.)
Usted puede encontrar este artículo en su versión original, en inglés, en la revista : 'Fidelio' - Summer-Fall 2002.
[1] Estos ejercicios pedagógicos forman parte de una serie llamada, "Riemann for Anti-Dummies" (Riemann para antitontos), que inició como un proyecto de estudio de los miembros y amigos del movimiento internacional de Lyndon LaRouche. Ver también, "The Division of the Circle and Gauss's Concept of the Complex Domain" (La división del círculo y el concepto de Gauss del dominio complejo), por Bruce Director, en 21st Century Science & Technology, número de invierno de 2001–2002 (vol. 14, núm. 14).
[2] Nota del traductor: comúnmente, dúnamis se ha traducido al español como potencia, término que conservamos para las exponenciales. Por ejemplo: 49 (4 a la novena potencia).
schiller@schillerinstitute.org
PO BOX 20244 Washington, DC 20041-0244
703-297-8368
Copyright Schiller Institute, Inc. 2001. Todos los derechos reservados