
Conferencias - Ciencia - Arte - Literatura - Noticias - Unase
Inglés - Inicio
Ciencia
Ejercicios Pedagógicos
Las raíces de Riemann

En diciembre de 1822 Carl Friedrich Gauss le envió a la Real Sociedad de Ciencia de Copenhague un documento titulado, “Solución general al problema de proyectar una parte de una superficie dada sobre otra superficie dada, tal que la imagen y el original sean similares en su más mínimo detalle”.
Es notable que el documento tuviera el lema: “Ab his vía sternitur ad maiora” (“Estos resultados preparan el camino para cosas más grandes”).
Y así fue. Casi treinta años después, en 1851, Bernhard Riemann le envió a Gauss su disertación de habilitación sobre las funciones de una variable compleja, la cual, junto con sus trabajos de 1857 sobre las funciones abelianas y las series hipergeométricas, desarrolló las implicaciones superiores del método que Gauss inició. Sin embargo, las implicaciones epistemológicas más profundas de estos resultados salieron a la luz en nuestra época, gracias a los descubrimientos de Lyndon LaRouche en la ciencia de la economía física, como en el caso de su reciente ensayo, “Cómo visualizar el dominio complejo”. En él se establece la perspectiva más ventajosa para revivir los descubrimientos de Gauss y Riemann.
Al principio, la Real Sociedad planteó para el llamado “Premio de Copenhague” un tema más limitado que el que en última instancia abordó Gauss. La pregunta original tenía que ver con resolver algunos problemas involucrados en la producción de mapas geográficos. A sugerencia de su colaborador, el astrónomo Heinrich Christian Schumacher, Gauss le propuso a la Real Sociedad la pregunta más general. Después de varios años sin que nadie ofreciera una solución seria a la pregunta que planteó, Gauss envió su propia solución y, por supuesto, ganó el premio.
Obviamente, Gauss estaba menos interesado en ganar el premio que en aprovechar la oportunidad de presentar los resultados más generales que desarrolló a lo largo de su vida, comenzando con su primer trabajo sobre la división del círculo y el teorema fundamental del álgebra. El reto de la Real Sociedad le brindó a Gauss la oportunidad de demostrar la amplitud del cálculo de Godofredo Leibniz, bajo el concepto del dominio complejo que Gauss desarrolló en esos primeros trabajos. Aunque esta aplicación solucionaba el problema práctico, más limitado, de producir mapas precisos, como Gauss indicó, en realidad se trataba de algo mucho más fundamental: específicamente del mejoramiento de la capacidad de la mente para entender y comunicar verdades concernientes a los principios imperceptibles que gobiernan el universo.
Las raíces del método de Gauss se hunden en lo profundo de la historia de los esfuerzos de la humanidad por aumentar su poder en y sobre la naturaleza, empezando con los primeros intentos de proyectar el espacio–tiempo de la certeza sensorial mediante el desarrollo de calendarios y mapas astronómicos y geográficos. Estos mapas no sólo expresaban los cambios visibles que reflejaban los movimientos de los cuerpos celestes. Los principios invisibles se reflejaban también en la forma de anomalías, paradojas y distorsiones. Así, cada mapa implica otro mapa que yace “detrás”, por así decirlo, del mapa visible.
Miembros del Movimiento de Juventudes Larouchistas, que han emprendido la tarea de observar el movimiento de Marte, enfrentan la clase de paradojas que surgen en el desarrollo de tales mapas. Sal y observa la salida de Marte por el este del firmamento. La composición de la imagen visual de Marte y las estrellas que lo rodean en el interior de la esfera celeste, da paso a una imagen mental, es decir, a un mapa. En el transcurso de la noche el movimiento de Marte y las estrellas en relación al observador cambia, formando una sucesión de imágenes mentales, lo que da paso a un mapa de los cambios en la sucesión de mapas nocturnos, o, en otras palabras, a un mapa de mapas. De una noche a la siguiente la imagen de Marte cambia su relación con respecto a las imágenes de las otras estrellas. Este cambio da paso a un mapa superior, a un mapa que refleja los principios subyacentes que gobiernan los cambios entre los mapas de las imágenes de la certeza sensorial. Este mapa superior se hace del todo inteligible, sólo desde la perspectiva del dominio complejo de Gauss y Riemann.
Aunque estas investigaciones son más antiguas, las raíces de nuestro conocimiento moderno comienzan con el esfuerzo de Tales de Mileto (624–547 a.C.) por proyectar la esfera celeste en un plano mediante la gnomónica, o proyección central. El método de Tales consistía en definir, sobre el plano, la imagen de cada punto de la esfera, dibujando una línea desde el centro de la misma, a través de la superficie, hasta que esa línea intersecaba el plano de la imagen (ver figura 1). (El mismo resultado puede demostrarse con medios físicos, usando una fuente de luz ubicada en el centro de una semiesfera transparente que proyecte las sombras de las figuras dibujadas en la semiesfera sobre una pared plana.)
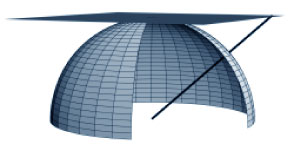
Figura 1
Esta proyección de inmediato nos plantea una paradoja crucial. Ciertas relaciones entre las imágenes de la esfera son diferentes de las que hay entre sus imágenes sobre el plano. Por ejemplo, la imagen de una triángulo esférico cuyos vértices son tres estrellas en la esfera celeste, es un triángulo rectilíneo sobre el plano. En consecuencia, las relaciones angulares entre las tres estrellas no pueden mantenerse en la imagen, pues los ángulos de un triángulo esférico siempre suman más de 180°, en tanto que de un triángulo plano siempre suman exactamente 180°.
Sin embargo, las relaciones mensurables entre las imágenes de las estrellas de la esfera celeste las determinan mediciones angulares, las cuales no aparecen representadas con precisión en la proyección gnomónica de Tales. La primera solución a este problema se le atribuye a Hiparco (160–125 a.C.), a quien también se le atribuye el descubrimiento de la proyección estereográfica. En este caso, la esfera se proyecta sobre el plano desde uno de sus polos (ver figura 2). (Esto puede demostrarse físicamente moviendo la fuente luminosa del experimento previo del centro de la esfera a su polo. Observa el cambio resultante en la relación entre las sombras.)
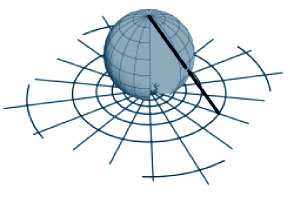
Figura 2
En esta proyección estereográfica, las líneas de longitud de la esfera se transforman en líneas radiales sobre el plano. Las líneas de latitud de la esfera se transforman en círculos concéntricos. Si consideramos que el punto que toca el plano es el polo “sur”, y que el punto de proyección es el polo “norte”, todos los círculos de latitud en el hemisferio “sur” se proyectan como círculos dentro del círculo que representa la imagen del ecuador. Por otra parte, los círculos de latitud en el hemisferio “norte” se proyectan fuera de este círculo. Las líneas radiales sobre el plano forman los mismo ángulos entre sí que las líneas de longitud de las cuales son imágenes. Sin embargo, el radio de los círculos concéntricos que son las imágenes de los círculos de latitud, aumenta de modo exponencial entre más se alejen del polo “sur” y más se acerquen al “norte” dichos círculos de latitud (ver figura 3).
En el caso de la proyección estereográfica, los ángulos entre las imágenes se mantienen.
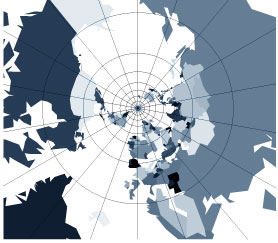
Figura 3
Otra proyección que conserva los ángulos fue desarrollada por Gerhard Kremer (1512–1594), conocido también como Gerhard Mercator. En la proyección de Mercator la imagen del ecuador es una línea recta, y las de los círculos de longitud son líneas perpendiculares distribuidas de forma homogénea a lo largo de ese ecuador. Las imágenes de los círculos de latitud son líneas rectas paralelas al Ecuador, pero la distancia entre ellas aumenta (ver figura 4).
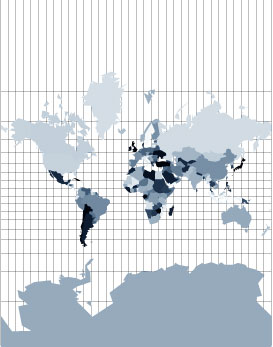
Figura 4
Esto se debe a que, en una esfera, las líneas de longitud se estrechan a medida que se acercan a los polos. De ahí que la proporción entre la distancia en la superficie de una esfera para un ángulo dado de latitud, y la distancia para el mismo ángulo sobre la superficie, cambie del ecuador a los polos (ver figura 5). Este cambio se refleja en la proyección de Mercator aumentando la distancia entre las líneas de latitud, de modo que la proporción entre los largos de latitud y longitud es la misma que en la esfera.
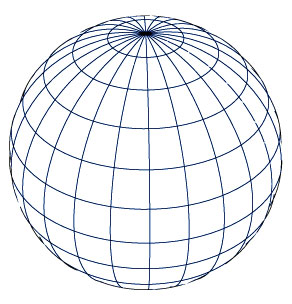
Figura 5
La proyección de Mercator, aunque totalmente diferente a la estereográfica, también conserva los ángulos. También tiene la característica de que la llamada “línea loxodrómica”, o la trayectoria que forma el mismo ángulo con todas las líneas de longitud, es una línea recta. Esto ejemplifica la clase de paradojas que surgen, pues la línea recta es la vía más corta sobre la superficie plana de la proyección. Pero, en la esfera, la vía más corta es un gran círculo, y la línea loxodrómica es una trayectoria en espiral llamada loxodromo, la cual es más larga que el gran arco circular (ver figura 6).

Figura 6
Así, a primera vista, el desarrollo de estas proyecciones que conservan los ángulos (una característica que Gauss más tarde llamaría “conformidad”) tiene una gran importancia para la representación de las imágenes del sensorio. No obstante, Gauss tenía algo mucho más importante en mente. Las distorsiones y paradojas que resultan de estas proyecciones, no sólo se deben a la representación visual, sino que reflejan algo “detrás” de lo visible. Al desarrollar medios generales para transformar una superficie en otra de conformidad, Gauss preparó el terreno para las investigaciones más generales de Riemann sobre la naturaleza de estas transformaciones en sí mismas, y sobre su relación con los principios que subyacen al sensorio.
Para esto, Gauss rechazó el euclidianismo reaccionario y a priori de Emanuel Kant. Para él, una “superficie” no es un objeto enclavado en un espacio euclidiano vacío que se extiende a infinito en tres direcciones. Más bien, una “superficie” se genera mediante alguna acción física. Por ejemplo, no medimos la esfera celeste con dos ángulos. La esfera celeste es una idea determinada de forma física, y generada por la acción física de rotación con respecto a la dirección de la fuerza de atracción de la gravedad y la dirección alrededor del horizonte de alguna dirección determinada de forma física, tal como la posición de la salida o la puesta del Sol.
En términos riemannianos, estos dos actos de rotación son los modos físicos de determinación de la esfera celeste. Si a estos modos de determinación los creara alguna otra acción física, producirían una superficie diferente. Esta es la base de una geometría determinada por medios físicos. Gauss demostró que la transformación de una superficie en otra, se logra al encontrar una función que transforma un par de modos de determinación en otro.
Esto es exactamente lo que sucede en una proyección estereográfica. Los dos modos de determinación, representados por círculos de latitud y longitud en la esfera, se transforman sobre el plano en círculos concéntricos y líneas radiales, respectivamente. En la proyección de Mercator, los mismos dos modos de determinación de la esfera se transforman de manera distinta, esto es, en líneas rectas. No obstante, ambas proyecciones son conformes. De modo que la característica de conformidad refleja un principio más general, que no es específico de una proyección particular.
Gauss reconoció que, para que una proyección sea conforme, tiene que transformar una superficie en otra igualmente en todas direcciones. Esto se expresa de forma geométrica en el hecho de que las imágenes de los círculos también son círculos. Podemos ilustrar esto en términos físicos de dos maneras. Imagina una superficie elástica, digamos, de goma. Si alargamos la superficie de forma proporcional en todas direcciones, entonces la forma de la imagen será la misma, solo que más grande. Si la alargamos en diferentes proporciones en diferentes direcciones, la imagen resultará distorsionada. La primera representa una transformación conforme, la última no.
Otro ejemplo físico. Toma una semiesfera de plástico transparente, y pégale círculos de diferentes tamaños con cinta adhesiva alrededor de lo que representaría un círculo de latitud sobre una esfera. Coloca una luz en el centro de la semiesfera. Observa las sombras. Los círculos se transforman en elipses. Ahora, mueve la luz al polo. Las sombras se vuelven más circulares, en especial las sombras de los círculos más pequeños. Esto ilustra la diferencia entre la proyección gnomónica y la estereográfica. En la primera, los círculos se alargan de forma diferente en diferentes direcciones, lo que produce elipses. Como tal, esta proyección no es conforme. En la segunda, los círculos se alargan para formar otros círculos, es decir, son conformes.
Esta característica de acción circular ya la había desarrollado Gauss desde 1796, como el principio de los números complejos, en su descubrimiento de la división del círculo y en su teorema fundamental del álgebra (publicado en 1799). Esto es, que un número complejo, mostraba Gauss, no se definía de modo arbitrario como la solución a una ecuación algebraica. Más bien, el número complejo expresaba ese acto de rotación, el cual trascendía y determinaba así toda magnitud algebraica posible. Por tanto, la transformación de un número complejo en otro era la de una acción rotacional en otra, precisamente la condición necesaria para que la proyección tenga conformidad.
Por esta razón, Gauss no consideró la superficie visible, sino su representación en el dominio complejo. Cada punto sobre la superficie corresponde a un número complejo, que a su vez está determinado por los modos físicos de determinación de la superficie. El transformar una superficie en otra requiere transformar los modos de determinación de una superficie en los modos de determinación de otra, la cual a su vez transforma cada número complejo de la primer superficie en un número complejo definido de la segunda. Esto es lo que Riemann después llamaría “una función de una variable compleja”.
Esto lo ilustraron los ejemplos anteriores de las proyecciones estereográficas y de Mercator. En el primer caso, los círculos de latitud y longitud que estaban distribuidos de forma homogénea alrededor de la esfera, se transformaron en líneas radiales y círculos concéntricos distribuidos de modo exponencial sobre el plano. Gauss señala que esto corresponde, en términos geométricos, a la transformación de la exponencial compleja (ver figura 7).
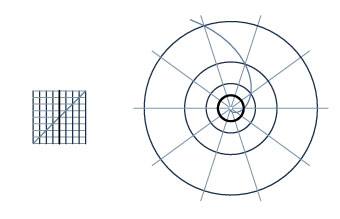
Figura 7
La proyección de Mercator corresponde a una transformación de círculos y líneas radiales distribuidos de forma homogénea en un entramado de líneas. Los radios se transforman en líneas verticales distribuidas de forma homogénea, y los círculos en líneas horizontales distribuidas de modo exponencial. Esto corresponde al inverso de la exponencial compleja, también conocida como el logaritmo complejo (ver figura 8). Para proyectar una esfera sobre un plano, Gauss aplicó estas transformaciones complejas a los modos de determinación de una esfera, esto es, a los dos modos de rotación.
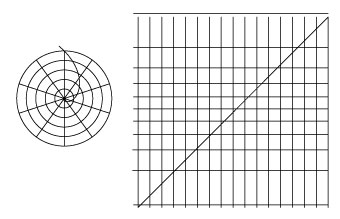
Figura 8
En su documento, Gauss demostró por qué esta clase de proyecciones tendría conformidad. Esto puede ilustrarse de forma geométrica observando el comportamiento de un pequeño cuadrado sometido a la transformación deseada. Gauss expresó esta condición geométrica mediante una fórmula en el lenguaje del cálculo de Leibniz, el cual Riemann reafirmó en su disertación de habilitación. Uno de los fraudes continuos de las matemáticas modernas, es que a ésta se le conoce como la fórmula “Cauchy–Riemann”, a pesar de que Agustín Cauchy no aportó nada a su desarrollo. Por precisión histórica, y por salud mental, ésta en realidad debería llamarse la relación Gauss–Riemann.
Todavía hay algo que se oculta tras bambalinas
schiller@schillerinstitute.org
PO BOX 20244 Washington, DC 20041-0244
703-297-8368
Copyright Schiller Institute, Inc. 2001. Todos los derechos reservados