
Conferencias - Ciencia - Arte - Literatura - Noticias - Unase
Inglés - Inicio
Ciencia y cultura
Artículos especiales
Pedagogía para jóvenes científicos
Llegando a la raíz cuadrada del problema matemático
No hay nada más seguro para evitar que los niños caigan en varias categorías de estupidez que existen en los Estados Unidos, y en otras partes, que ocuparlos en construcciones geométricas simples. Cualquiera puede hacer estas construcciones, con tal de que sepa escribir o dibujar, y ejercitar sus propios poderes cognoscitivos. Son estos poderes los que las prácticas normales del salón de clases rechazan, si no es que los destruyen.
Primero, dibuja un cuadrado.

Ahora, dibuja una raíz cuadrada.
![]()
No, no el símbolo conocido como el radical y la barra sobre él, el vínculum, sino lo que representa el símbolo: la propia raíz cuadrada.
Uf, ¿cuál es el problema? ¿Qué dices, que se te congeló el cerebro? Bueno, abordemos esto desde otro ángulo.
Multiplicando fracciones
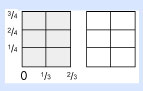
Mejor resolvamos el problema de multiplicación de fracciones más sencillo del mundo. Multiplica 1/2 por 1/2 usando el cuadrado que acabas de construir. Ahora, quizás lo primero que tu mente se pregunte cuando enfrente la tarea de multiplicar 1/2 por 1/2 sea, ¿un medio de qué?
¡Ajá! Tratemos de usar el cuadro para esto. Queremos encontrar 1/2 en este cuadrado, así que lo cortamos a la mitad.

Cuando cortamos verticalmente el cuadrado a la mitad, obtenemos una de nuestras fracciones, es decir, el primer 1/2.
Luego, cortamos el mismo cuadrado a la mitad de forma horizontal para conseguir la segunda fracción. Ahora, marca la base y el lado izquierdo del cuadrado 0, 1/2, 2/2, como se muestra.
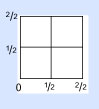
Este es el paso más importante, así que presta mucha atención: toma tus dos dedos índices y colócalos en la esquina marcada 0. Mueve solamente el índice derecho hasta la línea marcada 1/2 y ¡detente! Ahora, mueve ambos índices hacia arriba, hasta la línea marcada 1/2.
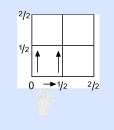
Colorea el pequeño cuadrado que cubriste con tus dedos, dentro de los límites de 1/2 por 1/2. Ahora numera los cuadrados.
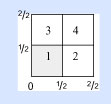
¿Qué acabamos de lograr?
Bueno, vemos que comenzamos con un cuadrado en blanco. Dividimos ese cuadrado a la mitad, lo que nos dio un cuadrado con dos partes. Luego dividimos de nuevo el cuadrado a la mitad, y obtuvimos un cuadrado con un total de cuatro partes: cuatro cuadrados pequeños. Y coloreamos uno de estos. Así, multiplicamos 1/2 × 1/2 = 1/4.
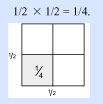
Ahora, practica el proceso anterior multiplicando 2/3 por 3/4, de forma geométrica. Con este método, en vez de memorizar, cualquiera puede ver de qué se trata la multiplicación. Ahora tenemos el modelo para multiplicar cualquier fracción por cualquier otra fracción. Pero también logramos algo que nos permite usar nuestra razón para adentrarnos en el estudio de la filosofía y de la física.
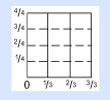
¿Cómo estuvo la cosa?
Ahora intentemos encontrar la raíz cuadrada de 0,81. Puedes representar esto usando el símbolo del radical y el vínculum encima de 0,81. Sí, ya sé que se supone que estemos contestando la pregunta de qué es una raíz cuadrada, ¡pero sé paciente!
![]()
Primero, ¿cuánto es 10 por 10? Todos saben que es 100. Bueno, dibujemos eso, un gran cuadrado de 10 unidades por 10 unidades, que tendrá 100 unidades dentro de él; es decir, 100 cuadritos.
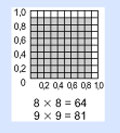
Bueno, ¿cuánto es 8 por 8? Todos saben que es 64. Y 9 por 9 es 81. Puedes ver cómo funciona esto en el cuadrado grande, moviendo tu índice sobre la base (o la parte superior) del cuadrado grande, 9 cuadritos, y el otro dedo, comenzando desde el mismo punto y hacia arriba (o hacia abajo), 9 cuadritos, y coloreando el área del cuadrado que cubriste.
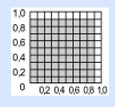
Podemos usar el mismo enrejado de 10 × 10 para las fracciones de 1. Al dividir todos los números de la base, 1, 2, 3, 4, etc., entre 10, tendremos 0,1, 0,2, 0,3, 0,4 y así sucesivamente. Y si hacemos lo mismo del lado izquierdo, contando 0,1, 0,2, 0,3, 0,4, etc., entonces podemos ver que 0,9 por 0,9 nos da 0,81. ¡Voilà! Encontramos que las raíces cuadradas de 0,81 son 0,9 por 0,9 (del mismo modo que las raíces cuadradas de 1/4 son 1/2 por1/2).
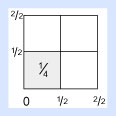
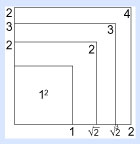
Además, ahora vemos que las raíces cuadradas vienen en pares iguales y que se construyen como los dos lados de un cuadrado. Y vemos que es imposible construir un cuadrado, sin al mismo tiempo también construir sus raíces cuadradas, las cuatro, tomando dos a la vez, ¡de la forma que quieras! Pero hay algo más.
Observa el lado del cuadrado que dividiste a la mitad dos veces (1/2 por 1/2). ¿Podemos dividir el lado de 0 a 1/2 a la mitad? Sí, esto nos da 1/4; Y podemos terminar el proceso dividiendo el lado de 1/2 a 2/2, para producir 3/4.
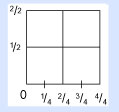
Ahora viene la verdadera dificultad conceptual. Marcamos el cuadro coloreado como 1/4, ¿no es así? Pero ahora tenemos otro lugar marcado como 1/4. ¿Qué significa esto? 1/4 es igual a 1/4, ¿o no?
¡Presta atención!
Presta mucha atención. Aquí es donde uno normalmente se despista. Tenemos dos entidades geométricas diferentes: una es un área cuadrada, 1/4 de cuadrado, y la otra es una línea geométrica, 1/4 de línea. Ambas aparecen partes del mismo cuadrado que construiste, y a ambas las numeramos como 1/4, pero son diferentes. Una vez que la mente entiende esta distinción, ¡el misterio se esfuma y lo reemplaza la alegría de dominar un proceso mental!
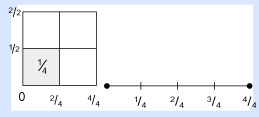
Nosotros podemos aclarar esto: ¡las líneas no tienen raíces cuadradas! No obstante, después de construir el cuadrado, vemos que el área del cuadrado determina la línea, a la que también se conoce como la raíz cuadrada. Sin embargo, la línea sólo es un lado del cuadrado. Si el niño, o el padre o el maestro, a este respecto, omite de la investigación de los números y las matemáticas la distinción entre el área y la línea, ambos marcados como 1/4, las matemáticas pierden sentido.
Veamos de nuevo el primer cuadrado vacío. ¿Puedes ver dónde están las raíces cuadradas? ¡Ellas también te miran, riéndose, por que las atrapaste!
Si a ti o a tu hijo los privan de esto, porque las escuelas han eliminado del curso esta geometría de los cuadrados, lo que sucede es que el estudiante se convence a sí mismo, o a sí misma, de que las "raíces cuadradas", y todas las matemáticas superiores, son misteriosamente difíciles y, por tanto, algo que sólo "gente inteligente" puede entender.
¿Les suena familiar? Es por estos actos de omisión que el estudiante se "lava el cerebro" él mismo, y reduce sus expectativas. El siguiente paso en estas matemáticas de autolavado cerebral, es que evites siquiera pensar.
Una nueva paradoja
Ahora, veamos con mayor detalle nuestro segundo ejemplo: 2/3 × 3/4, que, como descubrimos, es igual a 6/12.
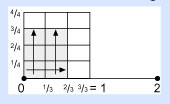
Dividimos esto en dos hileras, con seis cuadrados de un lado y los seis sombreados del otro. Así, podemos decir que 6/12 también es igual a un medio. ¡Pero espera! Algo no anda bien aquí.
En nuestro primer ejemplo, donde multiplicamos 1/2 × 1/2, empezamos con una cuadrado y terminamos con cuatro cuadrados pequeños, y nuestra respuesta fue uno de ellos, es decir, 1/4, pero todos los objetos eran cuadrados.
Aquí, empezamos con un cuadrado y terminamos con 12 rectángulos, y nuestra respuesta, 6/12 o 1/2, es un rectángulo. Ahora bien, ¿cómo hacemos un cuadrado de área 1/2? No un rectángulo, como el que tenemos ahora, sino un cuadrado de área 1/2. ¿Qué hacemos?
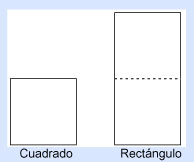
Si lees la historia del pobre Menón y su aventura con Sócrates, verás que tenemos el mismo problema que Menón y el niño esclavo enfrentaron; bueno, casi el mismo problema. De hecho, tenemos el problema contrario al de Menón, que debía construir un cuadrado el doble de grande que otro. En nuestro caso, debemos construir un cuadrado que sea la mitad de otro.
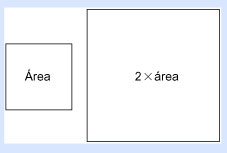
Hagamos esto abordando un problema aún más interesante: el temible teorema de Pitágoras (¡gulp!).
Este problema ha existido por varios miles de años, y quizás tu biblioteca tenga muchos libros sobre la historia de Pitágoras, su escuela y sus estudiantes. Algunos de ellos están llenos de dibujos interesantes, y (a veces) ecuaciones y fórmulas algebraicas que parecen muy complicadas. Pero juguemos un poco con lo básico.
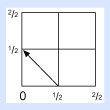
Primero, regresemos al problema de 1/2 × 1/2 y coloquemos algunos cuadrados en nuestro punto cero, como muestra la figura.
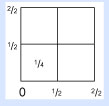
Ahora, dibuja una línea desde el punto inferior marcado 1/2 hasta el punto del lado izquierdo también marcado 1/2. Esta nueva línea se llama diagonal. La línea diagonal corta nuestro pequeño cuadrado —cuya área, como sabemos, es 1/4— a la mitad, formando dos triángulos.
Formando cuadrados perfectos con un círculo
Hagamos un paréntesis aquí, y formemos un "cuadrado perfecto" doblando un círculo.
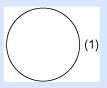
Primero, doblamos el círculo a la mitad, creando un línea llamada diámetro, que convierte el área circular doblada en un semicírculo.
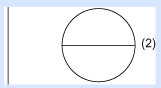
Ahora, dobla este semicírculo a la mitad, creando un segundo diámetro, a 90 grados del primero.
Si desdoblamos el círculo veremos una cruz en el centro, formada por la intersección de ambos diámetros.
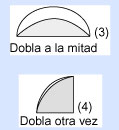
Ahora, dobla el círculo de nuevo y haz un tercer doblez por el arco, como muestra la figura.

Cuando abras el círculo verás adentro un cuadrado perfecto y cuatro triángulos, además de cuatro pequeños arcos del círculo sobre cada lado del cuadrado. ¿Empieza a aclararse todo?
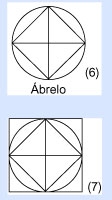
Regresemos a nuestro primer cuadrado, con sus dos pequeños cuadrados en el "punto cero" y con nuestra diagonal que va del punto 1/2 en la parte inferior al punto 1/2 del lado izquierdo.
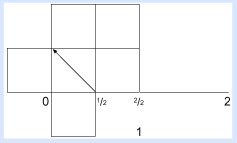
Ahora completemos nuestro trabajo dibujando las otras tres diagonales dentro de los otros tres cuadrados, y observa que las diagonales forman un nuevo cuadrado adentro del primero. ¿Cuál es el área del cuadrado que formamos con las diagonales?
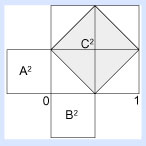
Ahora podemos plantear el teorema de Pitágoras: si tomamos un triángulo formado por los lados de tres cuadrados, podemos sumar las áreas de los dos cuadrados conectados por un ángulo recto (90 grados), y esa área total será igual a la del tercer cuadrado.
La forma más fácil de explicar esto es: "A cuadrada más B cuadrada es igual a C cuadrada". La "fórmula" se escribe A² + B² = C², y no es más que otro de los truquitos del álgebra usados para convencer a los estudiantes de que no tienen la inteligencia para convertirse en "verdaderos científicos" o para participar en temas importantes de "alto vuelo" intelectual. Repito mi advertencia: la mayoría de los libros de texto son totalmente engañosos a este respecto.
El problema más escandaloso y obvio es que ¡no hay cuadrados en los ejemplos de los libros de texto, sólo álgebra.
Pero, si regresamos al círculo en el que inscribimos un cuadrado, podemos amansar a nuestro monstruo con geometría. Recorta el cuadrado, y luego recórtalo por sus diagonales. Ahora tenemos cuatro triángulos. Pon el cuadrado sobre una hoja de papel y dibuja su contorno. Ahora, toma dos de los triángulos, acomódalos en la forma de un pequeño cuadrado y a los otros dos triángulos como otro cuadrado.
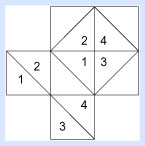
Ahora reconstruye el modelo y nombra las partes resultantes de nuestra pequeño rompecabezas: cuadrado A + cuadrado B = cuadrado C.
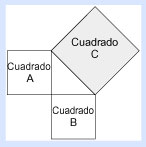
Si observamos los lados que forman y rodean al triángulo, podemos llamar a a los lados del primer cuadrado pequeño, b a los del segundo cuadrado, y c a los del cuadrado más grande. Entonces, sin olvidarnos de que el lado de un cuadrado es meramente el límite del área que encierra el cuadrado, y que esa área la construimos arrastrando el lado hasta cubrir la superficie necesaria, escribimos esa operación como a².
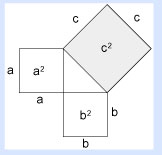
Ahora, podemos regresar y ver que, en nuestro primer ejemplo, podemos escribir 1/2 × 1/2 de la siguiente manera: 1/2², o un medio al cuadrado.
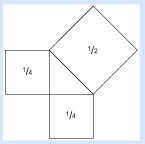
Ahora vemos lo que significa A², o a² (A cuadrada). También vemos que la fórmula A² + B² = C² implica recortar dos pequeños cuadrados y acomodarlos para formar un cuadrado más grande con las partes.
Los matemáticos investigan si esto siempre es verdad o no. Si intentamos hacer esto en una esfera, ¡no es cierto que A² + B² = C²!
Así que ya amansamos a nuestro monstruo. ¿O no? Veamos si realmente lo logramos.
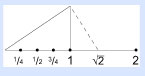
La raíz cuadrada de 1/2 no es un entero; 1/4 de área no es igual a 1/4 de línea. Así, estamos compilando una serie de paradojas y perspectivas mejores para abordar los números, y nuestra idea de qué son estos (y de qué son nuestros propios poderes mentales).
___________________________________________________________________________________
Artículo publicado en la revista Resumen Ejecutivo de EIR de la 2da.quincena de agosto de 2003 - Vol.XX, núm.16.
___________________________________________________________________________________
schiller@schillerinstitute.org
PO BOX 20244 Washington, DC 20041-0244
703-297-8368
Copyright Schiller Institute, Inc. 2001. Todos los derechos reservados