
Conferencias - Ciencia - Arte - Literatura - Noticias - Unase
Inglés - Inicio
Ciencia y cultura
Los tres niveles de la matemática: semillas del renacimiento

La escuela de Atenas (detalle de Arquímedes), por Rafael Sanzio
Por Jonathan Tennenbaum
El doctor Tennenbaum, director del Foro de Fusión Nuclear de Alemania y miembro del Comité Europeo de la Junta Internacional de Comités Laborales, hizo la siguiente exposición durante una conferencia del Instituto Schiller.
Alguna vez alguien dijo que el lenguaje es el fundamento del pensamiento, y que nadie puede pensar nada sin usar palabras. Cualquiera que sea la verdad que pueda haber en tal afirmación, no debemos olvidar que el lenguaje cambia y se desarrolla con el tiempo. En algún lugar de las profundidades de la mente humana nacen nuevos conceptos, y posteriormente les damos nombre. ¿Y qué de los lenguajes mismos? ¿Será posible que surja un lenguaje completo en la mente de una sola persona?
Hasta ahora no conocemos el desarollo inicial del lenguaje hablado. Las observaciones astronómicas que se registran en los cantos vedas, que se cantaban y que pasaron de generación en generación mucho antes de que se escribieran, fijan cronológicamente esos himnos en fechas no menos de 6.000 años antes de la actual; en ese entonces el sánscrito era ya un lenguaje completo y bien elaborado. La estructura básica de los lenguajes indoeuropeos, incluidos todos los lenguajes europeos modernos, y también el ruso y otros lenguajes eslavos, se establecio hace miles de años y no ha cambiado en lo fundamental desde entonces. Lo mismo se puede decir del chino; igualmente de los lenguajes semitas, como por ejemplo el hebreo y el árabe, y otros. A pesar de que han ocurrido muchos cambios, los lenguajes que hablan los seres humanos en la actualidad son, en esencia muy antiguos.
No se puede decir lo mismo ni de la matemática ni de la música. La matemática, como parte de un lenguaje cuyo desarrollo se correlaciona muy directamente con el crecimiento del poder del hombre sobre la naturaleza en los últimos 2.500 años, ha evolucionado en una serie de revoluciones, en las cuales su contenido y su forma han crecido y cambiado de una manera más bien dramática. Este desarrollo más reciente del componente matemático (o en un sentido más amplio, del componente geométrico) del lenguaje , es mucho más accesible para nosotros que el período inicial de desarrollo del lenguaje hablado. Esperamos que del lenguaje matemático podamos aprender algo de gran valor respecto a la mente humana.
Si observamos el panorama del desarrollo de la matemática en los últimos 2.500 años, hay dos acontecimientos específicos que se destacan, en tanto revoluciones de un tipo relativamente más profundo.
El primero de estos acontecimientos ocurrió hace aproximadamente 550 años, y tiene que ver con el trabajo de Nicolás de Cusa y el inicio del Renacimiento Dorado en Europa en los siglos 15 y 16. El segundo, mucho más reciente, data de hace 100 años cuando Georg Cantor elaboró el transfinito, culminando con su descubrimiento de lo que él bautizó con el nombre de las series alef.. Estos dos acontecimeintos marcan una división de la matemática en tres niveles o dominios, tanto desde un punto de vista de su desarrollo histórico como el de su existencia actual. Estos tres niveles de la matemática se correlacionan con tres formas diferentes de reflexión sobre el universo.
El primer nivel, “A”, podemos identificarlo históricamente con la denominada geometría euclidiana de los griegos, tal y como la uso Arquímedes, por ejemplo. El segundo nivel, “B”, se caracteriza por el gran desarrollo iniciado con la introducción de lo que se conoce como funciones no algebraicas o funciones trascedentales. Ese desarrollo empezó, fundamentalmente, con Nicolás de Cusa, fue trasmitido a través de los geómetras del Renacimiento, tales como Brunelleschi y Leonardo da Vinci; y floreció completamente en las últimas décadas del siglo 17, en particular, con los trabajos de Huygens, Leibniz y Bernoulli. Siglo y medio después encontramos que Riemann ya estaba llevando a su límite este dominio de la matemática, y poco después Cantor verdaderamente abrió paso hacia el nuevo universo del transfinito. El tercer nivel, “C”, el dominio caracterizado por el tipo de pensamiento encarnado en las series alef de Cantor, aún está en pañales , en su etapa inicial. Es un nene muy bello.
Propongo que demos un breve vistazo a estos tres niveles, no considerados en sí mismos, sino para comprender mejor la clase de cambio en la manera de pensar que ocurre al pasar de un nivel al siguiente; es decir, cómo llegamos de “A” a “B”, y luego de “B” a ”C”.
Antes de empezar con nuestro tema permítanme advertirles que no es mi propósito aquí llegar a una precisión de tipo formal. Todo lo contrario; estoy obligado a emplear una forma metafórica de hablar. Espero que al final quede claro por qué esto es necesario.
En segundo lugar, si algunas de las ideas y términos son extraños para muchos de ustedes, no se dejen desconcertar. Estos temas son simples en lo fundamental, aunque, en realidad, bastante profundos; además es un poco difícil condensarlos en una charla corta. Simplemente acudan a los representantes del Instituto Schiller más cercanos y acósenlos hasta que se los expliquen. O si no son capaces, a lo mejor pueden trabajar con ellos. No duden en desafiarlos; son gente muy valiente.
El nivel “A”
La forma de matemática ampliamente conocida como la geometría euclidiana se codificó, como aproximación de un sistema deductivo lógico, alrededor del año 300 antes de Cristo. Aunque los famosos trece libros de los elementos de Euclides, en ciertos aspectos importantes, sólo representan distorcionada y unilateralmente lo que era realmente la geometría griega, podrían bastar como ejemplo negativo de lo que aquí me propongo; esto es, ubicar la clase de limitaciones o restricciones que Nicolás de Cusa superó al lanzar la revolución que condujo al siguiente nivel de la matemática, el nivel “B”.
La geometría euclidiana aborda la cuestión de la organización del espacio y de todas las formas espaciales posibles, e intenta reducirlas a elementos fundamentales que se relacionan entre sí de varias maneras conforme a ciertas reglas o leyes.
El elemento básico es el punto. Este se considera como un tipo de idea obvia que no requiere demostración. El segundo elemento es la línea recta, de nuevo considerada como entidad autoevidente. El tercero es el plano. Y entre las relaciones básicas entre estos, la geometría euclidiana postula, por ejemplo, que por dos puntos dados sólo puede pasar una línea recta (ver la Gráfica 1).

Además del punto, la línea recta y el plano, la geometría euclidiana introduce otro elemento: el círculo, que conlleva un concepto de longitud, distancia o medida. El círculo, considerando su circunferencia, pareciera consistir de todos los puntos que se encuentran a cierta distancia fija de un punto fijo que es el centro. En el espacio la forma correspondiente es la esfera. De esta manera tenemos estas especies de objetos: punto, línea recta, plano, círculo, esfera.
Y ahora tratamos de contruir o explicar todas las formas en el espacio a partir de estos elementos. Esto conduce de inmediato a las famosas construcciones con regla y compás.
Construimos varias clases de triángulos, ya que son las más simples de las formas (ver la Gráfica 2). Después, rectángulos y polígonos de varios tipos, y las formas sólidas correspondientes. Examinamos las relaciones de proporción y magnitud, primero en tanto segmentos definidos por pares de puntos sobre una línea. Inventamos formas de reproducir o dividir cualquier segmento en dos, tres o cualquier número de segmentos iguales, para poder sumar y restar longitudes y multiplicar y dividirlas según las leyes de la proporcionalidad. Todas estas operaciones se pueden expresar mediante una taquigrafía llamada álgebra.
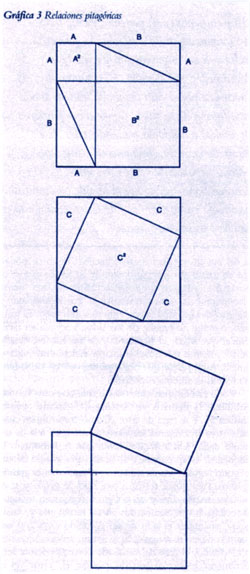
Luego pasamos a las áreas y volumenes . Descubrimos relaciones tan bellas como la que se atribuye a Pitágoras, que se refiere al área de los cuadrados formados en los lados de un triángulo en que uno de sus ángulos es recto, y que se puede demostrar dividiendo un cuadrado grande de dos formas diferentes (ver la Grafica 3). Y así, vamos avanzando.
Pero en la geometría euclidiana elemental de las figuras planas, encontramos ya muy pronto paradojas y anomalías; problemas que se pueden formular muy fácilmente, pero que no se pueden resolver dentro del mundo de la geometría euclidiana misma. Esas anomalías marcan los límites externos de la geometría euclidiana, que no alcanza a explicar del todo su propia existencia; hay fenómenos que en ella no tienen explicación.
Por ejemplo, encontramos el fenómeno de la inconmensurabilidad entre segmentos de distintas líneas. Podemos compartir la perplejidad de los primeros geómetras al darse cuenta de que, cuando la diagonal y el lado de un cuadrado se dividen en un número arbitrario de segmentos iguales, nunca se llega a una medida común, a un segmento que quepa un número exacto de veces en ambos. Este descubrimiento lleva a la creación de varias especies de números en un intento de “cerrar” las brechas que hay en la línea entre las fracciones ordinarias o números racionales.
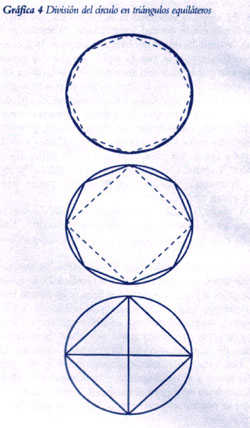
Otra anomalía tiene que ver con la división de un círculo mediante la inscripción de polígonos regulares, de lados iguales (ver la Gráfica 4). Es sencillo construir un triángulo equilátero en un círculo; también es fácil hacer un cuadrado, cuyos vértices dividen la circunferencia del círculo en cuatro arcos iguales. También podemos construir un polígono regular de cinco lados, el pentágono, aunque la construcción es de una forma curiosamente diferente, que sólo se puede entender a cabalidad desde un punto de vista más avanzado. El exágono, o polígono regular de seis lados, vuelve a ser fácil. Pero el que sigue, el heptágono, de siete lados, desafía completamente cualquier solución exacta con regla y compás. Aquí parece que nos topamos con un verdadero límite de la geometría euclidiana.
Todo está íntimamente relacionado con otro famoso problema: la llamada cuadratura del círculo (ver la Gráfica 5).
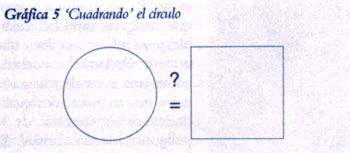
Y se trata de esto: ¿Cómo construir un cuadrado cuya área interna sea exactamente igual a la de un circulo dado? Un enfoque obvio, que se remonta a la antigüedad, es aproximarse al círculo por medio de un polígono regular con un número suficientemente grande de lados. Para quien conosca este tipo de geometría, es cuestión sencilla dividir un polígono regular en triángulos rectángulos, reorganizarlos en un rectángulo y, finalmente, encontrar el lado de un cuadrado cuya área sea igual a la de ese rectángulo. Si se usa un polígono inscrito en el círculo, el área del cuadrado correspondiente será ligeramente menor al área del círculo; el “error” es la pequeña área entre los lados del polígono y los arcos subtendidos del círculo.
De la misma manera, si circunscribimos un polígono al círculo, obtenemos un área que es ligeramente mayor. El promedio de los dos valores nos daría una buena aproximación. Por ejemplo, encontramos al geómetra chino Liu Hiu, el año 264 después de Cristo, más o menos, que usó un polígono de 3.072 lados para obtener un valor aproximado con presición hasta el quinto decimal.
Hasta donde sabemos, Arquimedes, alrededor del año 250 antes de Cristo, fue el primero en considerar no uno o dos, sino una serie completa de polígonos inscritos y circuncritos con un número de lados cada vez mayor. El procedimiento más sencillo es empezar con un triángulo o con un cuadrado, e ir duplicando el número de vértices y de lados. Basta bisectar los arcos circulares o lados correspondientes de cada polígono sucesivo. Así, por ejemplo, a partir de un cuadrado inscrito, se puede construir el octágono, un polígono de 16 lados, de 32, de 64, y así sucesivamente (ver la Gráfica 6).
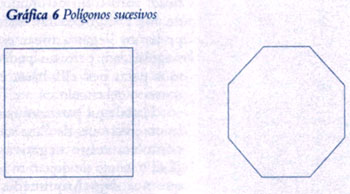
Arquímedes llamó a este enfoque el “método de exhaución”, y en realidad es fácil ver que el área del polígono muy rápidamente “llena” el área circular conforme aumenta el número de lados. El área restante –el “error”, como lo hemos llamado–, se reduce a menos de la mitad cada vez que doblamos el número de lados del polígono. Hipotéticamente, si se sigue lo suficiente por esta serie, se puede reducir el error hasta la mínima magnitud que queramos.
Estrictamente hablando, sin embargo (y esto es lo que más mortifica), nunca se llagará en forma precisa a un verdadero error cero. Siempre hay una pequeña discrepancia, representada por los pequeños pedacitos en forma de media luna que quedan entre cualquier polígono y el círculo (ver la Gráfica 7).

Mucho más dramática es la situación que surge si tomamos la esfera en lugar del círculo. En este caso tratamos de aproximarnos a la superficie de la esfera mediante superficies limitadas por secciones de planos; en otras palabras, por poliedros. Y entre estos, los de propiedades más parecidas a la esfera son los poliedros regulares, análogos a los polígonos regulares, que tienen caras simétricas e idénticas. He aquí que hallamos que sólo se pueden construir cinco de esos poliedros, los famosos “sólidos platónicos”: el tetraedo, el cubo, el octaedro, el dodecaedro y el icosaedro. En realidad todos se reducen a uno solo, ya que todos los sólidos se pueden derivar rápidamente del dodecaedro. No existe un procedimiento sencillo de duplicación, análogo a lo que hicimos con lo polígonos, y en todo caso ninguno que preserve las propiedades de simetría. Aquí aparece, pues, en forma muy tangible e irreductible, una discrepancia fundamental entre el mundo lineal de los planos y las líneas rectas, y el mundo curvo de la esfera.
La revolución de Cusa
Nicolás de Cusa apareció a mediados del diglo 15 y empezó a reeleborar lo que Arquímedes había hecho 1.700 años antes, y a llevar el trabajo de Arquímedes a sus límites conceptuales. Cusa se preguntó, regresando al enfoque de la “exhaución”: ¿podemos considerar que los polígonos convergen hasta identificarse con la circunferencia del círculo? O, usando una forma paradójica de hablar, ¿se hacen los polígonos iguales al círculo “en el infinito”? ¿Podríamos decir, entonces, que el círculo es un polígono con un número infinito de lados? Nicolás de Cusa respondió a estas preguntas con un categórico ¡no!
Cusa subrayó que la diferencia entre el círculo y los polígonos no es simplemente de magnitud, sino de cualidad o especie. Nicolás lo planteó de la siguiente manera:
Puesto que los polígonos no son magnitudes de la misma especie del círculo, aunque podamos siempre encontrar un polígono que se aproxime más al círculo que un polígono dado, aun asi es cierto que no se puede obtener lo absolutamente grande, ni en posibilidad ni en existencia, entre cosas que pueden ser o más grandes o más pequeñas. En realidad, el área del círculo es el máximo absoluto relativo a las áreas de los polígonos inscritos, que pueden ser mayores o menores y por lo tanto jamás pueden llegar al área circular, así como ningún número puede jamás lograr el poder abarcante de la unidad ni el poder compuesto de lo simple.
Exploremos un poco más el asunto. Observen que en los vértices de cualquier polígono hay un cambio súbito de la dirección del lado; en este sentido, una discontinuidad (ver la Gráfica 8a).
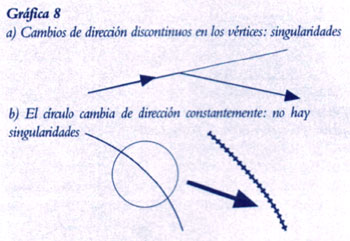
El perímetro del círculo, en cambio, cambia de dirección continuamente, y en ese sentido todos los lugares geométricos de la circunferencia son completamente equivalentes entre sí (ver la Gráfica 8b). De esa forma, la existencia de discontinuidad en los vértices distingue absolutamente al polígono del círculo. ¿Y qué pasa cuando aumenta el número de lados del polígono? Las discrepancias que representan los puntos de discontinuidad direccional crecen en número y densidad. Por ejemplo, tras duplicar cincuenta veces el número de lados a partir de un cuadrado, llegamos a una situación en la que un grado de arco del círculo correspondiente contiene ya más de diez billones de puntos de discontinuidad del polígono. Evidentemente, aunque las áreas de los polígonos se van aproximando a la del círculo en simple cantidad total, sus perímetros se apartan cada vez más desde el punto de vista cualitativo.
Esto tal vez podría expresarse diciendo que hay un “no sé qué” muy delgadito que separa al círculo no sólo de cualquier polígono individual, sino del conjunto o suma de todos los polígonos habidos y por haber. Es algo que ni tiene magnitud expresable, al menos en el sentido común y corriente, pero de todas formas es algo que existe. Es de un grosor menor que cualquier cantidad medible, pero rehusemos decir que es cero. Podemos concebirlo como una zona de transición entre dos mundos, dos cualidades de existencia: de la poligonía a la circularidad. Es lo que llamamos una singularidad. Partiendo del mundo de los polígonos tan sólo podemos llegar a tocar esa singularidad, pero no podemos pasar por ella hasta el universo del círculo.
Hasta aquí pareciera que las observaciones de Cusa son completamente negativas. ¿Está tratando de quitarnos lo que nos dejó Arquímedes? Pero agreguemos una última observación, y veremos que lo que acabamos de obtener es muy valioso: El hecho de que el polígono nunca puede llegar a ser círculo, ni siquiera con un hipotético “número infinito” de lados, nos fuerza a concebir en forma totalmente diferente el círculo y toda la geometría.
Si el círculo es inaccesible desde el mundo de los polígonos, ¿de dónde proviene? Pues el círculo, en cuanto forma, es la simple huella de un movimiento circular que en sí mismo es resultado de la acción de rotación (ver la Gráfica 9). Y Nicolás de Cusa consideró el movimiento rotatorio como la única y más directa reflexión del ser –es decir, del proceso de creación del universo mismo– en el dominio visible de la forma y el movimiento. Esa correspondencia se demuestra, como posteriormente lo subrayó Cusa, por lo que se denomina la característica isoperimétrica o de acción mínima de la acción rotatoria.
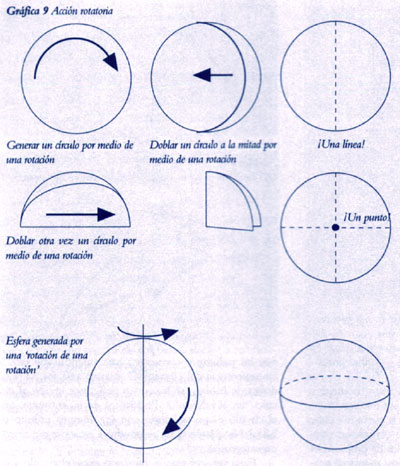
Esta nueva visión del círculo pone a toda la geometría euclidiana bajo una nueva luz, al mismo tiempo que la trasciende. Observamos que las formas elementales de la geometría euclidiana se derivan todas de la acción circular. Por ejemplo, si empezamos con la acción circular, generamos, en primer lugar, el círculo. Pero si al círculo recién creado se le aplica de nuevo la rotación, de tal forma que el círculo se pliegue sobre sí mismo, se obtiene entonces, como singularidad del proceso de plegado una línea recta que es el diámetro del círculo. Si se dobla de nuevo, se obtiene un segundo diámetro que interseca al primero lo que crea un punto.
Con más pliegues –más grados de rotación– se van generando los vértices de los polígonos de los que antes nos valíamos para tratar de aproximarnos al círculo: el ángulo no es otra cosa que el resultado de la rotación. Pareciera, pues, que la rotación permea a toda la geometría, como sustancia subyaciente, pero al mismo tiempo yace apenas más allá del alcance de la propia geometría euclidiana.
A partir de las observaciones puramente negativas de Cusa, que identifican una barrera absoluta que separa al círculo de todos los polígonos, hemos trascendido los límites de la geometría euclidiana y empezamos a ascender a un ámbito más elevado de la matemática. Ahora comienza el desarrollo de un nuevo tipo de geometría en el que prima el cambio, el movimiento, el lugar de la forma en sí. Es el movimiento lo que genera las formas, y una cualidad de cambio que determina las características de lo que llamamos, en su conjunto, espacio-tiempo físico.
El nivel ‘B’
![]()
Ahora bien, si miramos el trabajo de Leonardo da Vinci en el diseño de máquinas, en anatomía, hidrodinámica y su concepto de ondas de luz y de sonido, etc., queda claro que Leonardo estaba impregnado de la concepción geométrica que apenas comenzamos a desarrollar. El desarrollo formal de una geometría fundamentada en la acción circular empieza mucho más tarde, con los trabajos de Christian Huygens, Gottfried Leibniz, y Johann Bernoulli. Dicho en las palabras de Leibniz, este trabajo “abre la fuente y el cofre del tesoro de las funciones no algebraicas”.
Todo lo que se hace, en esencia, es descubrir un universo entero de formas o especies de movimiento, partiendo tan sólo de la acción circular. Este principio demuestra muy bien la construcción de Huygens de los diferentes cicloides.
Tomemos un círculo y hagamos rodar por su circunferencia, ya sea por dentro o por fuera, un segundo círculo más pequeño (ver la Gráfica 10-a). Entonces, el movimiento de un punto fijo, cualquiera que sea, en el círculo pequeño, describe una curva, que en general se llama cicloide. ¿Qué pasa aquí? La curva se genera por dos especies simultáneas de acción circular: primero, el centro del círculo pequeño está girando en torno al centro del círculo grande; y, segundo, el círculo pequeño, a su vez, gira en torno a su propio centro. Obsérvese que cuando los radios de los dos círculos son conmensurables (es decir, que guardan relación de números enteros), entonces los cicloides cierran, y los puntos singulares, llamados cúspides, definen las posiciones de los vértices de los polígonos regulares.
Quizás los polígonos debieran considerarse simples sombras de estas entidades superiores, los cicloides cerrados. Al mismo tiempo, vemos que la mayor parte de la aritmética elemental y la teoría de los números está contenida en la conducta de estos cicloides. Surge un caso interesante cuando los radios de los cicloides no son conmensurables; entonces las cúspides forman una serie uniformemente densa por toda la circunferencia del círculo grande (ver la Gráfica 10-b).
Para el caso especial de un círculo pequeño que rueda sobre una línea recta, considerada ésta como el borde de un círculo “muy grande”, la distancia rectilínea entre cúspide y cúspide es igual a la circunferencia del círculo menor (ver la Gráfica 10-c). Con esto, quienes tengan alguna pericia en geometría verán fácilmente como “cuadrar el círculo”.
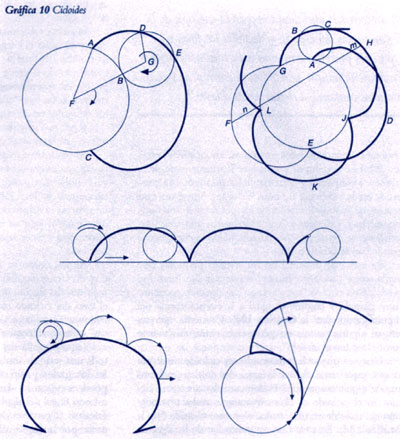
Una vez que se ha construido un cicloide mediante lo que podríamos llamar la rotación doble, ¿qué nos impide seguir avanzando? Podemos rodar un tercer círculo en el cicloide o, alternativamente, rodar una porción del cicloide en un círculo, o en otro cicloide (ver la Gráfica 10-d). En cada caso un punto fijo de la curva en movimiento describe una nueva curva. Obviamente este proceso se puede continuar indefinidamente.
El mismo principio, de otra manera, subyase la construcción de Huygens de la llamada involuta de una curva (ver la Gráfica 10-e). Tomemos cualquier círculo, atémosle en algún punto una cuerda y envolvámosle una parte alrededor del círculo. Ahora desenvolvamos lentamente la cuerda, manteniendola tensa. El movimiento del extremo de la cuerda describe una nueva curva, una especie de espiral, llamada la involuta del círculo originario.
A primera vista, este movimiento pareciera completamente diferente del que genera al cicloide. Pero si lo examinamos más detenidamente no encontramos otra cosa que una combinación de dos grados de acción de rotación, pues en cualquier momento del proceso puede verse que el final de la cuerda gira alrededor del punto en el que la cuerda toca el círculo. En ese momento ese punto se ha convertido en lo que los geómetras llaman el centro de la curvatura. Al mismo tiempo, ese centro de contacto se está moviendo, está rotando a lo largo del círculo originario. De esta manera tenemos dos grados de rotación.
El aspecto adicional, si se le compara con el cicloide, es que el radio del segundo grado de rotación –la distancia entre el final de la cuerda y el punto de contacto con el círculo– crece constantemente. Si avanzamos un poco más aprendemos a generar envolturas de curvas, incluida la famosa “cáustica” producida por los rayos de luz reflejados en un espejo curvo (ver la Gráfica 11-a).
¿Qué nos impide ahora abrir aún más el “cofre del tesoro” de las nuevas curvas?
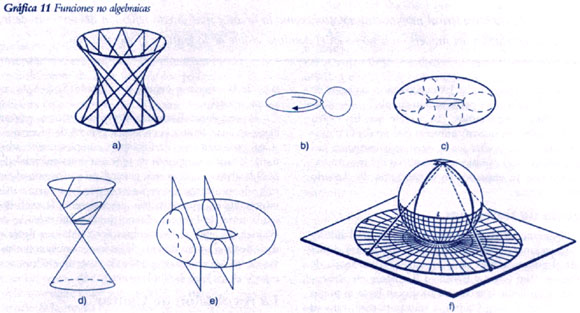
Al aplicar las operaciones de involución y de rodar una curva sobre otra, a la totalidad de las curvas ya generadas a partir de un punto dado, se produce una nueva generación de curvas. Se crea una especie de proceso evolutivo. Pero observemos que la acción de rotación permanece en todos los casos como el “principio hereditario” subyacente al proceso de generación.
Ahora, como ya lo subrayo Leibniz, las curvas de esta creciente familia no se pueden describir con los métodos del álgebra ordinaria. El álgebra fracasa ya desde el caso del cicloide más sencillo. Leibniz bautizó, pues, esta nueva familia con el nombre de curvas “no algebraicas” o “trascendentales”.
La taquigrafía del álgebra sólo sirve si se introduce toda una serie de símbolos y operaciones nuevas, como las integrales y diferenciales de Leibniz. Pero no se puede explicar ni dar cuenta de ninguna dentro del mundo lineal del álgebra misma; uno siempre tiene que referirse al proceso de generación externo al álgebra, razón por la que el cálculo de Leibniz causó tanta conmoción entre los matemáticos, y la sigue causando hasta la fecha.
Pero esto es apenas una primera muestra del cofre del tesoro de las funciones no algebraicas.
Tomemos ahora un círculo y hagámoslo rotar sobre su diámetro; generamos una superficie: la esfera (ver la Gráfica 11-b). Fijemos un círculo pequeño en ángulo recto a la circunferencia de un círculo más grande. Hagamos girar el círculo mayor: generamos un toro (ver la Gráfica 11-c). Fijemos cualquier otra curva al círculo grande y hagámoslo girar: se crea el tipo general de superficie que se conoce como superficie de revolución. Esta nueva fuente de funciones trascendentales fue aprovechada especialmente por Gaspard Monge y sus colaboradores en la Ecole Polytechnique de fines del siglo 18.
Por ejemplo, al rotar una línea obtenemos conos e hiperboloides (ver la Gráfica 11-d).
Ahora tomemos cualquier superficie de revolución, y cortémosla con una serie de planos. La intersección de la superficie con cualquier plano es una nueva curva.
Los que conozcan de geometría sabrán que al cortar un cono obtendremos, según el corte que decidamos, círculos de varios tamaños, elipses, parábolas e hipérbolas anchas o delgadas.
Al cortar un toro, por ejemplo, por planos paralelos, se obtiene una familia de curvas de un orden superior que, hasta donde yo sé, aún no se les ha dado nombre (ver la Gráfica 11-e). Pero cualquiera de ellas se puede tomar como base para un proceso posterior de generación, formando superficies de revolución de ellas, o produciendo sus involutas. De esta manera, una sola curva puede generar, vía su superficie de revolución, toda una familia de curvas y nuevas superficies (ver la Gráfica 11-f); y así, ya las contiene todas en forma potencial. Si lo pensamos un poco, de veras es algo extraordinario.
Baste lo dicho, a modo de rápida incursión en el mundo de las funciones no algebraicas. Antes de seguir en nuestra travesía, permítanme señalar que esta generación de curvas no algebraicas de un orden cada vez más elevado es al mismo tiempo una exploración de posibles diseños de máquinas.
Tan pronto se introduce mediante la actividad de la mente, como lo hizo Cusa, el concepto de una nueva calidad de cambio, y el universo manifiesta su concordancia con experimentos cruciales de los que realizó Leonardo da Vinci y posteriormente, en el caso de la luz, Römer y Huygens, entonces ya estamos listos para una revolución tecnológica. Esto fue exactamente lo que ocurrió con el rápido desarrollo de las máquinas, anticipado por Leonardo da Vinci y que tomó vida explosivamente con la revolución industrial. Fue por esta razón que Leibniz y Huygens se refirieron a las funciones no algebraicas como “curvas mecánicas”: son curvas descritas por las piezas de máquinas. Existe mucho más que una simple analogía entre la generación de órdenes superiores de curvas y superficies, y el progreso de la tecnología.
Reflexionando sobre esto, tenemos que preguntarnos: ¿Cuáles son los límites de este mundo de las funciones no algebraicas? Observemos primero lo siguiente:
El universo de las funciones no algebraicas es uno en que el concepto de cambio conlleva una idea de movimiento. Pero también hay un concepto implícito de cambio de cualidad o especie de movimiento. Cuando se procura entender el universo físico desde el punto de vista del concepto de movimiento, es preciso dividir en especies las cualidades del movimiento.
Una característica de las funciones no algebraicas es que se desarrollan por especies. Ya tuvimos un atisbo de ello en la distinción que hizo Cusa entre los polígonos y el círculo. La elaboración de las curvas no algebraicas lleva a una gran multiplicidad de nuevas especies de funciones, y ocasiona una pregunta de mayor alcance: ¿Será posible enumerar esas especies mediante algún tipo de función?
En otras palabras, supongamos por un momento que el concepto de la acción circular multiconexa, eleborada en las formas que he indicado, cubre todos los modos de cambio en el espacio-tiempo físico. ¿Podrá ahora definirse ese espacio-tiempo mediante una función que incluya todas las cualidades o especies de movimiento generados por la acción circular?
También preguntamos: ¿Es posible que haya otro tipo de cambio en nuestro universo que no sea el movimiento sino que podría ser la causa más inmediata del movimiento y del cambio en la cualidad del movimiento? Con esto ya entramos en el problema del llamado campo cuántico.
Teoría de Funciones
El intento de abarcar toda la gama de posibilidades de las funciones no algebraicas y establecer sus relaciones desde el punto de vista de la especie, se llama teoría de funciones. Carl Gauss y Bernhard Riemann , en particular, lograron llevar la teoría de funciones hasta el punto en que llegó Georg Cantor a transportarnos, con su extraordinaria intuición, al mundo del transfinito.
Basten por ahora algunas breves indicaciones. Gauss adoptó el método de relacionar todo a la esfera, donde cualquier traslación ocurre en forma de rotación. Esto conduce, entre otras cosas, a lo que se llama el dominio complejo. Cuando se redefinen las funciones trascendentales desde el punto de vista de ese dominio esférico o complejo, se eliminan ciertos rasgos artificiales del ordenamiento del espacio euclidiano, y se revela en forma maravillosa la organización interna de estas funciones.
Siguiendo esos lineamientos de la obra de Gauss, Riemann mostró cómo caracterizar una función del dominio complejo tan sólo desde el punto de vista del tipo y la conGráficación de sus singularidades, sin relacionarlas con magnitudes escalares. Esto reduce la determinación de las especies de funciones trascendentales a un problema del analisis situ o topología.
Riemann también intentó caracterizar el proceso por el cual una función puede “saltar” de una especie inferior a una superior. La introducción de una nueva singularidad en una función corresponde al caso en que un proceso físico es conducido hasta sus límites y más allá, en tanto esos límites parecen ser determinados por una tasa finita de propagación de la acción dentro de ese proceso. En ese momento se llega a lo que los físicos llaman un cambio de fase: surgen nuevas cualidades en el proceso, acompañadas (en el feliz caso de ser un proceso negatoentrópico) de un aumento del número de grados de libertad. Riemann mostró cómo se pueden construir funciones que pasan por una serie de cambios de fase, de la especie o estado S1 al estado S2, a S3, y así sucesivamente.
Por esa época Riemann, Weierstras y otros estaban llevando a sus límites el concepto general de función”. ¿Cuál sería una serie de funciones completamente arbitraria, la serie más general de funciones matemáticas? ¿Es posible abarcar el tipo más general de curvas con algún método uniforme de representación? La forma más importante de representación que la gente veía era la llamada serie de Fourier. Esencialmente, el método de Fourier era explicar los cambios dentro de una función dada desde el punto de vista de las fases cambiantes relativas de un número muy grande de procesos cíclicos; una especie de cicloide múltiple generalizado.
La revolución de Cantor
Cantor empezó su trabajo sobre la teoría de las funciones estudiando el problema de representar una función arbitraria de la llamada serie de Fourier, y encontró que la representación de Fourier tenía una falla frecuente: por lo general, habrá un dominio singular en el que una función dada no concuerda con su serie de Fourier. Entonces, tal como indico Cantor, las especies de funciones se pueden ordenar según su grado de irrepresentabilidad, como lo refleja la densidad de singularidades en cada intervalo. Esto implica que las especies de funciones tienen un rango u ordenamiento natural conforme va aumentando la densidad de singularidades.
Este tipo de cosas ya las vimos en nuestra discusión del círculo y los polígonos. Cada uno de los polígonos representa una especie, con 4, 8, 16 y más singularidades así sucesivamente. Estas especies estón ordenadas de manera natural en el orden ascendente del aumento de la densidad de sus singularidades –los vértices– en la circunferencia del Círculo.
Obsérvese además que cada especie contiene a la anterior en el siguiente sentido: el cuadrado se obtiene de inmediato uniendo los lados del octágono, por ejemplo, de dos en dos. Nótese también que cada especie superior se obtiene por la simple acción de doblar el número de lados.
Ahora bien; ya hemos observado que el círculo permanece, digámoslo así, por encima de toda la serie de especies de polígonos y de cada uno de ellos, generándolos a todos por acción circular. Así, al parecer se completaría el ordenamiento si agregamos, después de todas las especies de polígonos, por así decirlo, la especie circular:
[P4, P16, P32 ...], ...? ..., C
Los corchetes significan todo el sistema ordenado de especies de polígonos cuyo número de lados son potencia de dos. Cusa insistió en que el círculo es absolutamente diferente de cada uno de los polígonos y de la suma de todos ellos. Ello plantea la interrogante de si no habrá otra especie ubicada en el espacio entre el círculo y los polígonos. Cantor responde definitivamente esta pregunta con un “sí”. Sin tratar de representar una Gráfica concreta de cómo sería la forma de esa especie, simplemente imaginemos una especie hipotetica S que será la “primera especie posterior o superior a la de los polígonos” y que representa únicamente aquella porción del poder de acción universal que sea exactamente suficiente para generar todos los polígonos.
Algo parecido se puede apreciar en un dibujo en perspectiva de un ferrocarril que se va al infinito como tratando de llegar a una estrella, pero converge en cambio en un punto de fuga sobre el horizonte, abajo de la estrella, que sigue infinitamente lejos. El punto de fuga es la especie S; la estrella es la especie de la acción circular.
Lo que hizo entonces Cantor fue desarrollar lo que podríamos llamar una teoría general de tipos de ordenamiento de las especies. En esa teoría general se deja completamente a un lado la naturaleza particular de las especies que se ordenan, y sólo se examina la relación mutua en que se ordenan. Así, podemos aplicar el método de Leibniz de analisis situ.
Empecemos con la serie simple de especies
S1, S2 ..., Sn
en la que S2 es el sucesor natural de S1, S3 el sucesor natural de S2, etc. Tal serie podría continuar indefinidamente, como los polígonos, agregando grados de libertad en cada paso.
La cualidad de cambio encarnado en la serie S1, S2, S3 ..., que es la causa inmediata de la progresión de cada especie hacia la siguiente, constituye una especie superior a cualquiera de los términos individuales de la serie. Llamemos a esto la especie superior S’. Siguiendo a Cantor colocamos S’ inmediatamente arriba o después de la serie S1, S2, S3 ..., en cuanto es su sucesor natural:
[S1, S2 ...], S’
Observen algo interesante que Cusa ya señaló en el caso del círculo y los polígonos: pareciera como si un número literalmente infinito de pasos separara la primera especie, S1, de la especie superior S’. Ese tipo de infinidad numérica en realidad es apenas un reflejo paradójico del hecho que no se puede llegar a S’ , la especie superior, partiendo de las especies inferiores Sn tomadas en sí y por sí mismas; es decir, separadas del principio universal creativo (el absoluto) que es el mismo en todas las cosas y permanece por encima de todo.
Ahora bien; la especie S’, no siendo en absoluto, en sí misma puede progresar. Ahora podemos empezar a ver por qué Cantor utilizó el término “transfinito” para describir este tipo de ordenamiento. Así, empezando con S’ tenemos la serie anterior.
[S1, S2, S3 ...], S’, S’2, S’3 ...
De nuevo habrá una especie superior sucesiva S”, que encarna el principio de cambio generando esta segunda serie y constituye la siguiente especie después de esa serie:
[S1, S2, S3 ...], [S’1, S’2, S’3 ...], S”
Podemos seguir así con S’, S”, S”’, y así sucesivamente, pero el principio es claro. Refelexionen en eso por un momento: “el principio es claro”. Ya nuestra mente ha formado el concepto de una serie superior S, S’, S”, S”’ ... que trasciende la primera serie original, y también la segunda y la tercera y la cuarta y las demás en nuestro ordenamiento de series. Esa serie superior encarna en sí misma una cualidad superior de cambio, especie que podríamos denominar T y que yace fuera del alcance de todas y cada una de las especies del tipo S, constituyéndose en sucesor necesario en su ordenamiento.
([S1, S2 ...], [S’, S’1, S’2 ...], S”, S”1, S”2 ...], {S”’, S”’1, S”’2 ...], ...), T
Pero T, por supuesto, empieza una nueva serie, y así sucesivamente. Estamos explorando las primeras bases de lo que Cantor bautizó con el nombre de números de segunda clase.
Ahora surge una nueva idea en nuestra mente. Todo el proceso por el cual empezamos con la primera especie S1 y llegamos por fin a T, ¡podría aplicarse también a T ! Claro que ese ya no sería el mismo proceso, literalmente, pero sería equivalente en el sentido del concepto de analisis situ de Leibniz. Así, formalmente hablando, podemos asociar otra copia de todo el ordenamiento a T, simplemente reemplazando en todas partes S por T. La siguiente especie superior, que encarna la cualidad de cambio de toda la serie T, la llamaríamos U.
¡Ajá! Si reflexionamos sobre todo el proceso de ir de S a T como un tipo específico de transformación , y el mismo tipo nos lleva de T a un nivel U aún más elevado, entonces tenemos el concepto de una serie S, T, U, V, etc., y una cualidad de cambio encarnada en toda esa serie, que está por encima de todos los procesos que hasta ahora hemos discutido. Ya vemos el camino hacia un nivel más alto de desarrollo transfinito.
Para continuar esta exploración sin que nos dé vértigo y nos caigamos de la cumbre, se necesitaría una especie de mapa de la clase general de ordenamientos que van surgiendo. Cantor lo proporcionó (o por lo menos hizo el intento) con su teoría de los tipos ordinales transfinitos y una clase especial de notación, que juega en los ordenamientos transfinitos un papel similar al conocido sistema decimal para los números naturales. Pero esa construcción formal no es esencial para nuestra presentación.
Se reconocerán algunas semejenzas entre lo que venimos haciendo y lo que hicieron Leibniz, Huygens y Gaspard Monge al abrir el manatial de las funciones no algebraicas. También es del mismo tipo de cosa en que se entra cuando exploramos el Motivführung y el principio de las variaciones musicales. De hecho, el transfinito de Cantor no es otra cosa que el analisis situ, el principio subyaciente de ordenamiento de todos estos tipos de procesos de desarrollo.
Pero tadavía no hemos llegado a lo más importante; hasta ahora sólo le hemos puesto el andamiaje. Empezamos con la pregunta de si es posible enumerar todas las especies posibles mediante una función matemática única, tal y como Riemann y otros plantearon implícitamente el problema. La estremecedora respuesta a esta pregunta abre el camino a la famosa serie de los alef de Cantor, y conduce nuestro viaje a feliz término.
Reflexionemos un poco sobre el tipo de proceso que empezamos a desplegar. En cualquier punto de ese proceso, todo el ordenamiento de las especies comprendidas hasta ese momento se pueden enumerar implícitamente; simplemente tenemos que volver a trazar los pasos que nos llevaron hasta allí. ¿Y qué del principio que nos sigue impulsando a extender el proceso cada vez más? Ese proceso lo impulsamos formando en nuestra mente el concepto de una nueva cualidad de progresión, a la cual le damos el nombre en tanto función matemática.
Al desarrollar el proceso fundamentados en este concepto, nos damos cuenta de sus limitaciones o su relativa finitud, y al mismo tiempo se forma un nuevo concepto. Mas tan pronto se concibe como función una serie de desarrollo –es decir, una progresión ordenada del tipo que hemos indicado– en ese punto exacto empieza una nueva fase de desarrollo más allá de esa función.
¡Ajá! Eso quiere decir que el potencial, el poder de este proceso de formación de conceptos, trasciende el concepto mismo de función, al menos en el sentido de función que hemos heredado del nivel “B” de la matemática. A la usanza de Cantor, llamamos “alef cero” (N 0) al poder de ese concepto ordinario de función, enumeración u ordenamiento de valores. Luego llamamos “alef uno” (N 1) al poder del concepto de un principio generador del proceso transfinito que acabamos de describir, mediante un proceso de concebir funciones cada vez superiores, proceso que por su naturaleza misma trasciende cualquier función posible.
Ahora bien, observemos que N 1 es el sucesor necesario de N 0, aunque están separados por lo que podría parecer una gran brecha insalvable y casi indescriptible.
Observemos además que N 1 es absolutamente inalcanzable por medio de lenguaje alguno. No podemos comunicarlo de manera directa, lineal, sino que tan solo puede ser evocado, hecho surgir, en el proceso creativo mental de la mente de otra persona. N 1, en este sentido, sólo se puede transmitir por medio de metáforas.
Pero aún así –y esto es fundamental– N 1 es un objeto de pensamiento definido de manera muy precisa. Se trata de la acción creativa, o de la formación creativa de conceptos en general, en un sentido muy vago; tampoco de trata de Dios. Pero es ese objeto de pensamiento inmediatamente superior a cualquier concepto de función de la matemática ordinaria, de función, y que inmediatamente genera ese concepto. Podemos decir que N 1 es el tipo de nivel de realidad física que inmediatamente confina desde afuera al espacio-tiempo físico.
Al haber convertido ahora esta capa limitante inmediata en objeto de la conciencia, impulsamos la física a nuevo dominio: un renacimiento científico.
En cierto sentido, el concepto de función heredado del nivel “B” de la matemática, ahora juega el papel que jugaron los polígonos para Nicolás de Cusa. Eso nos dice también que el espacio-tiempo normal de la física matemática actual está limitado externamente por algo diferente, de lo que apenas ahora venimos a formarnos un concepto.
Hemos llegado a un Stretto.
¿Hará falta decirles que hay alef superiores y que en realidad hay toda una serie transfinita de éstos? Pensemos en el paso de N 0 a N 1. Eso caracteriza, creo que muy bien, el paso revolucionario de Cantor del nivel “B” de la matemática, el dominio de la teoría de funciones, al nivel “C”, fuente y cofre del tesoro del transfinito.
Ahora comparemos ese paso al paso que dio Nicolás de Cusa, del nivel “A” al nivel “B”. ¿Acaso no hay una especie de equivalencia superior entre estas dos revoluciones? Ahora regresemos y miremos lo que Lyndon LaRouche ha estado escribiendo sobre las hipótesis superiores y la acción de formular hipótesis sobre las hipótesis superiores.
¿No sugiere esto que estamos en el umbral de un nuevo renacimiento? Ya hemos dado los primeros pasos. No faltará quién diga: ¿Qué? ¿Un nuevo renacimiento? Están locos? ¡No lo he visto en la televisión! Pues no lo verán, al menos al principio. Pero no olviden que para cosechar las flores debemos tener primero las semillas. Y éstas las estamos sembrando ya.
schiller@schillerinstitute.org
PO BOX 20244 Washington, DC 20041-0244
703-297-8368
Copyright Schiller Institute, Inc. 2001. Todos los derechos reservados